내용 기반 추천시스템
- 내용 기반 추천시스템의 원리
✔️ 각 사용자가 구매/만족했던 상품과 유사한 것을 추천하는 방법(동일한 장르의 영화 추천, 같은 학교 동기들을 친구로 추천하는 것 등...)
✔️ 시스템의 4가지 단계
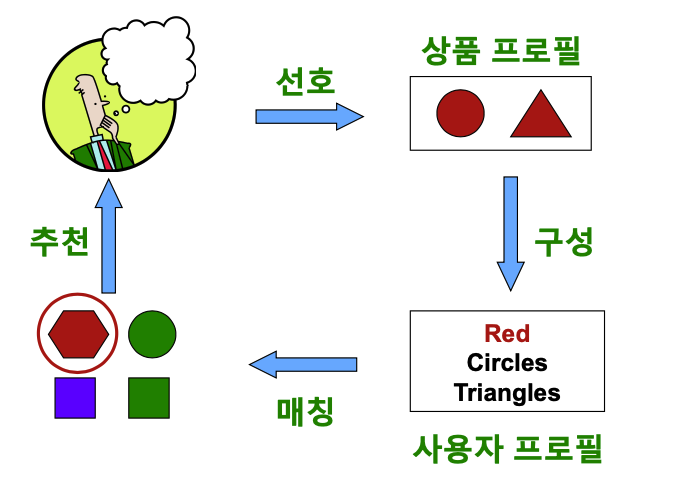
출처: Naver BoostCamp AI Tech - edwith 강의
1️⃣ 사용자가 선호했던 상품들의 상품 프로필(Item Profile)을 수집하는 단계
👉 상품 프로필이란 해당 상품의 특성을 나열한 벡터이다.(예 - 원-핫 인코딩의 사용)
2️⃣ 사용자 프로필(User Profile)을 구성하는 단계
👉 선호한 상품 프로필을 선호도를 사용하여 가중 평균하여 계산한다.(원-핫 인코딩된 벡터들을 가중평균)
3️⃣ 사용자 프로필과 다른 상품들의 상품 프로필을 매칭하는 단계
👉 사용자 프로필 벡터 와 상품 프로필 벡터가 있다고 가정할 코사인 유사도(벡터의 내적 식에서 유도) 를 계산하여 그 유사도를 비교한다.(코사인 유사도 값이 높을수록 두 벡터 사이의 각도는 작다.)
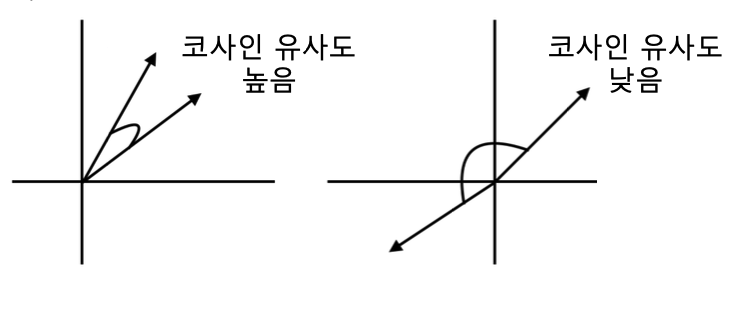
출처: Naver BoostCamp AI Tech - edwith 강의
👉 코사인 유사도가 높을 수록, 해당 사용자가 과거 선호했던 상품들과 해당 상품이 유사함을 의미
4️⃣ 사용자에게 상품을 추천하는 단계
👉 코사인 유사도가 높은 상품들을 추천
✔️ 장점
1, 다른 사용자의 구매 기록이 필요하지 않음
2, 독특한 취향의 사용자에게도 적용이 가능
3, 새 상품에 대하여 추천이 가능
4, 추천의 이유를 제공 할 수 있다.(상품 프로필과 사용자 프로필을 사용하여 추천을 해 주기 때문)
✔️ 단점
1, 상품에 대한 부가 정보가 없는 경우 사용 할 수 없다.
2, 구매 기록이 없는 사용자에게는 사용할 수 없다.
3, Overfitting으로 지나치게 협소한 추천을 할 위험이 있다.(하나에 치우친 추천을 할 수 있다.)
협업 필터링
✔️ 비슷한 취향을 가진 사람들을 판단의 기준으로 삼아 추천하는 방법
✔️ 시스템의 3가지 단계
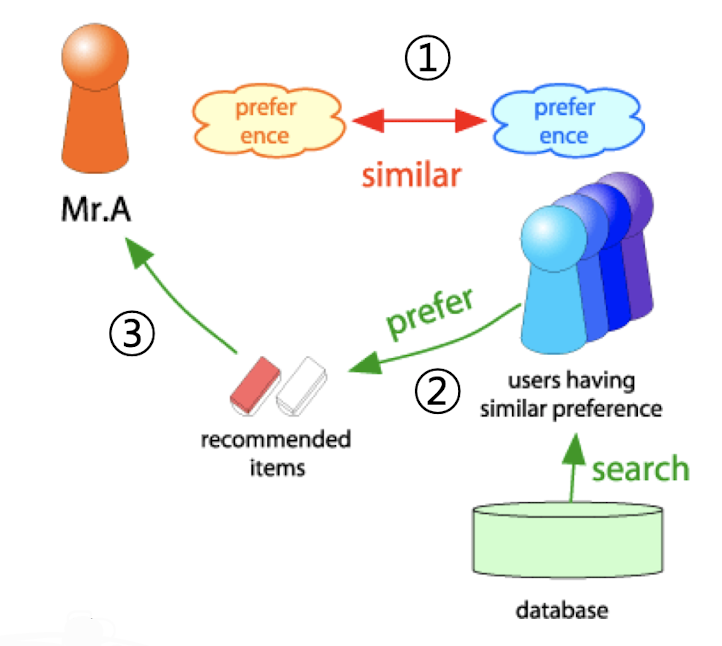
출처: Naver BoostCamp AI Tech - edwith 강의
1️⃣ 추천의 대상 사용자를 라고 가정
2️⃣ 다음 단계로 유사한 취향의 사용자들이 선호한 상품을 찾음
3️⃣ 마지막으로 해당 상품을 에게 추천한다.
✔️ 취향의 유사성은 상관 계수(Correlation Coefficient)를 통하여 측정한다.
➡️
👉 사용자 의 상품에 대한 평점 :
👉 사용자 가 매긴 평균 평점 :
👉 사용자 와 가 공동 구매한 상품들 :
✔️ 취향 유사도의 예시
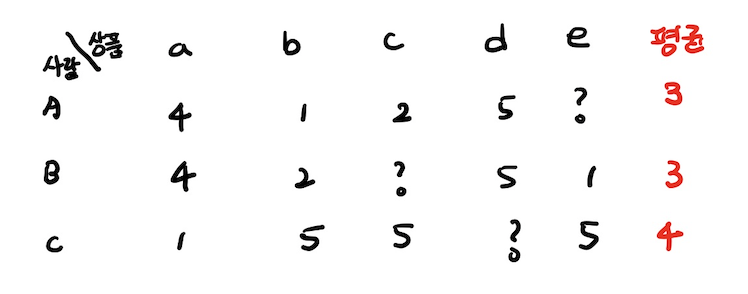
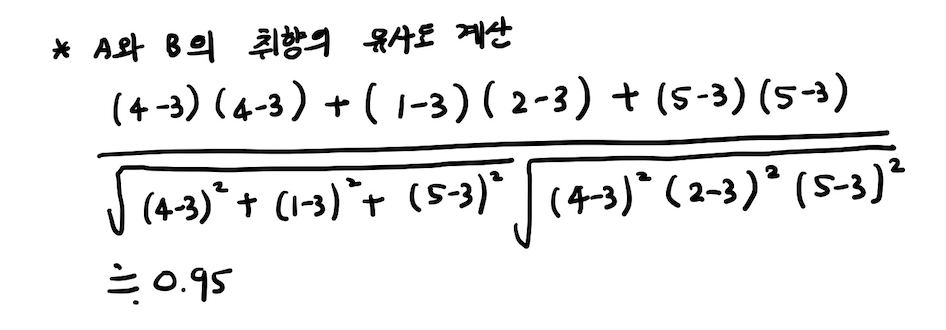
❗️ 둘의 취향은 매우 유사하다.
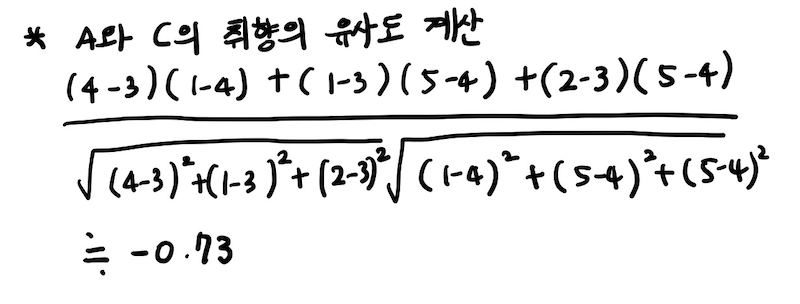
❗️ 둘의 취향은 매우 상이하다.
✔️ 취향의 유사돌르 가중치로 사용한 평점의 가중 편균을 통해 평점을 추정
👉 사용자 의 상품 에 대한 평점을 를 추정하는 경우
1️⃣ 상품 를 구매한 사용자 중 와 취향이 가장 유사한 명의 사용자 를 뽑는다.
2️⃣ 평점 는 해당 수식을 이용하여 추정
➡️
⭐️ 취향의 유사도를 가중치로 사용한 평점의 가중 평균을 계산 ➡️ 추정한 평점이 가장 높은 상품들을 에게 추천
✔️ 장점
1, 상품에 대한 부가 정보가 없는 경우에도 사용이 가능
✔️ 단점
1, 충분한 수의 평점데이터가 누적되어야 효과적
2, 새 상품, 새로운 사용자에 대한 추천 불가능
3, 독특한 취향의 사용자에게 추천이 어렵다.(취향의 유사도가 높은 사람이 존재하지 않을 수 있기 때문)
추천 시스템의 평가
- 추천 시스템의 평가는 훈련 데이터와 평가데이터로 분리 후 훈련데이터를 이용해서 평가 데이터의 평점을 추정하고 실제 평가 데이터를 비교하여 오차를 측정하고 이를 평가 지표로 사용하게 된다.
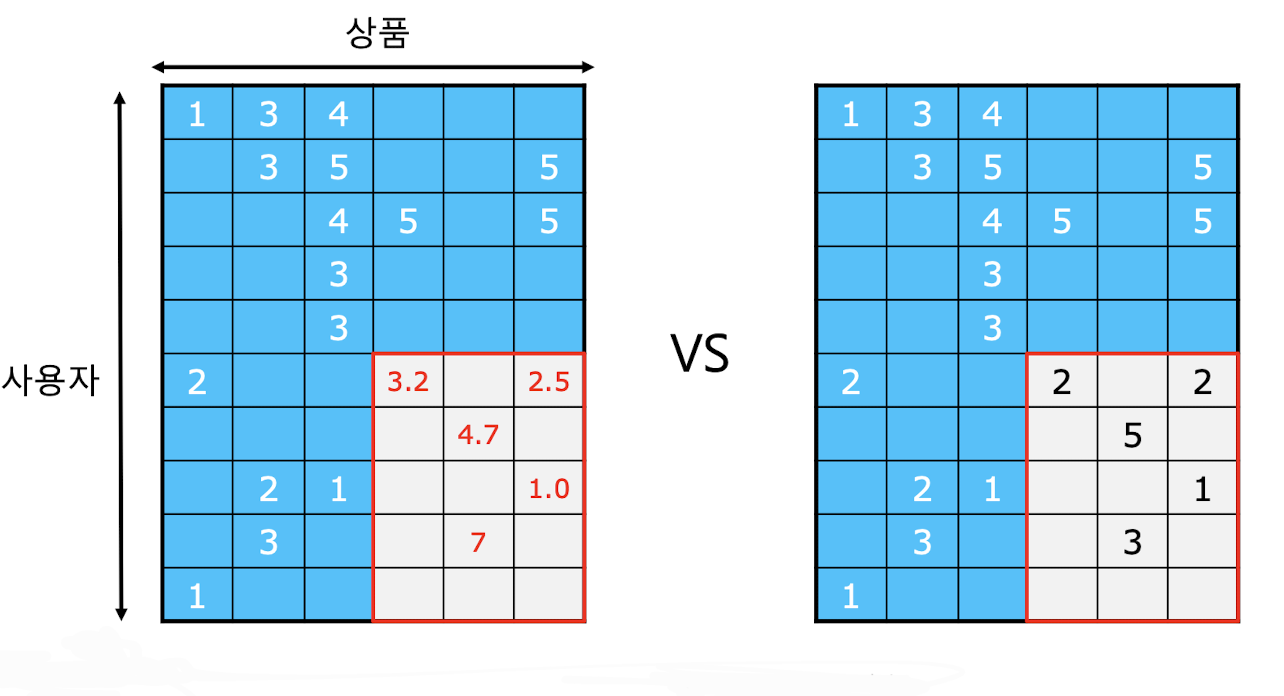
출처: Naver BoostCamp AI Tech - edwith 강의 - 평가 지표
오차를 측정하는 지표로는 다음과 같은 방법들이 존재한다.
✔️ 평균 제곱 오차(Mean Squared Error, MSE)
➡️ (이때, 평가 데이터 내의 평점들의 집합은 )
✔️ 평균 제곱근 오차(Root Mean Squared Error, RMSE)
➡️
✔️ 추정한 평점으로 순위를 매긴 후, 실제 평점으로 매긴 순위와의 상관 계수 계산
✔️ 추천한 상품 둥 실제 구매로 이루워진 것의 비율을 측정
✔️ 추천의 순서 혹은 다양성까지 고려하는 지표들도 사용
Reference
Naver BoostCamp AI Tech - edwith 강의
