벡터
-
벡터란?
숫자를 원소로 가지는 list(리스트) 또는 Array(배열) -
열벡터와 행벡터

-
백터는 공간의 한 점을 나타낸다.
- 방향과 길이를 가지고 있음
- 1차원으로 표현 가능 ([1], [2,3], [4,5,6] ...)
- 원점으로부터 상대적 위치를 표현
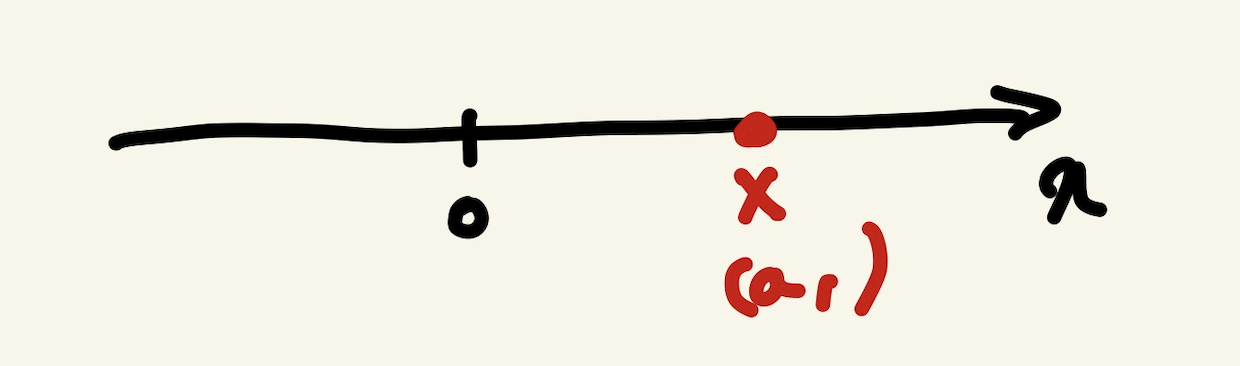
1차원의 공간
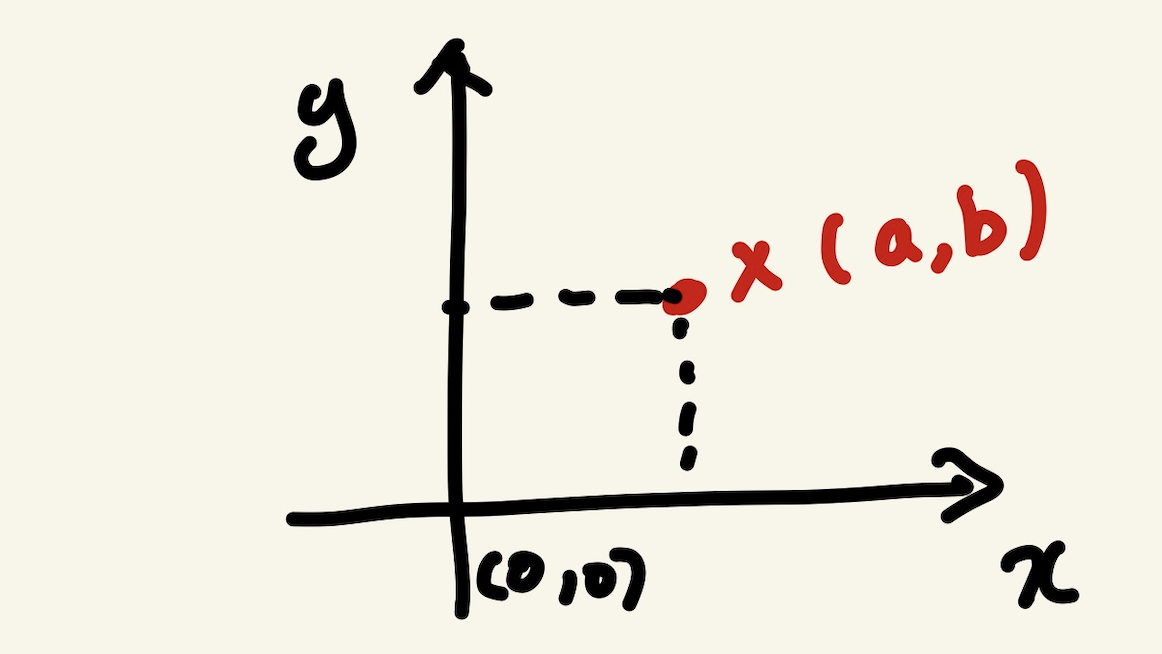
2차원의 공간

3차원의 공간
- 벡터의 상수배
- 백터에 숫자를 곱해주면 길이가 변함
- 음수를 곱해주면 반대방향으로 방향이 전환
- 0보다 작은 수를 곱해주면 길이가 줄어듬
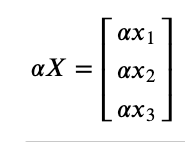
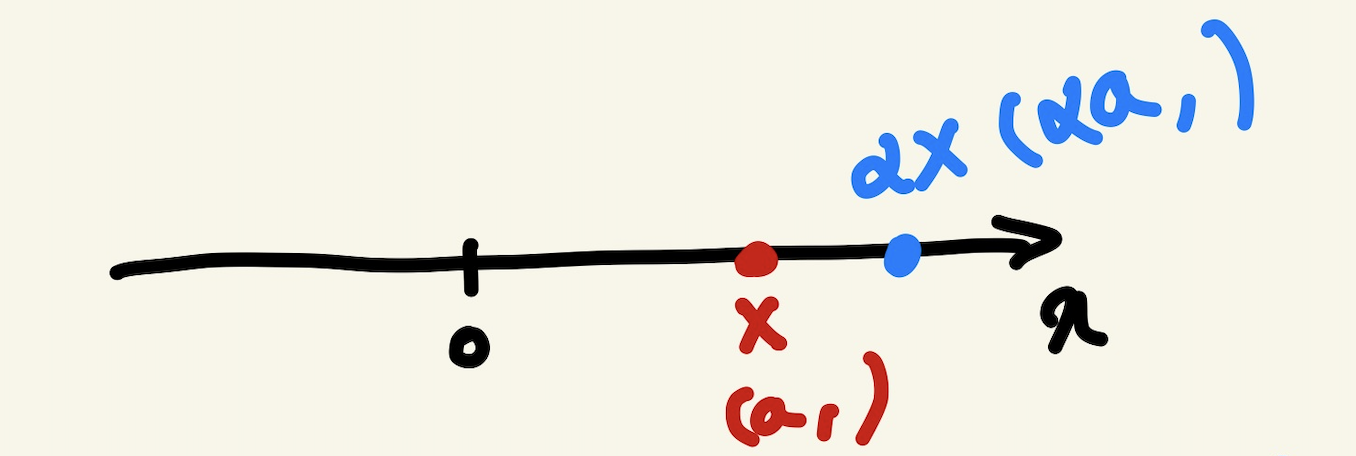
1차원

2차원
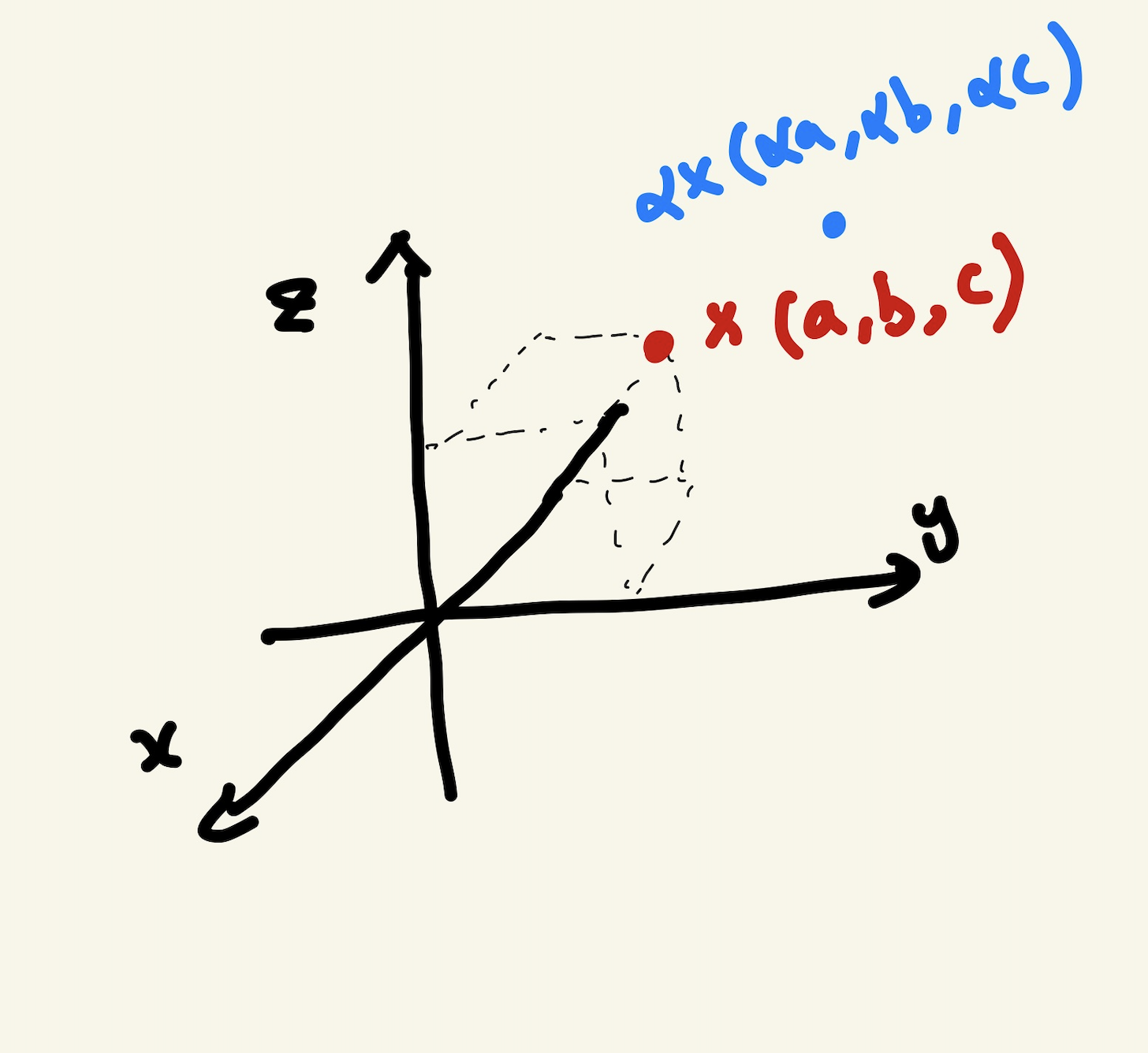
3차원
벡터의 연산
-
ndarray(numpy)를 이용하여 덧셈, 뺄셈, 성분곱이 가능
-
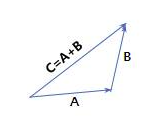
벡터의 덧셈
다른 벡터로부터 상대적 위치이동을 표현
-
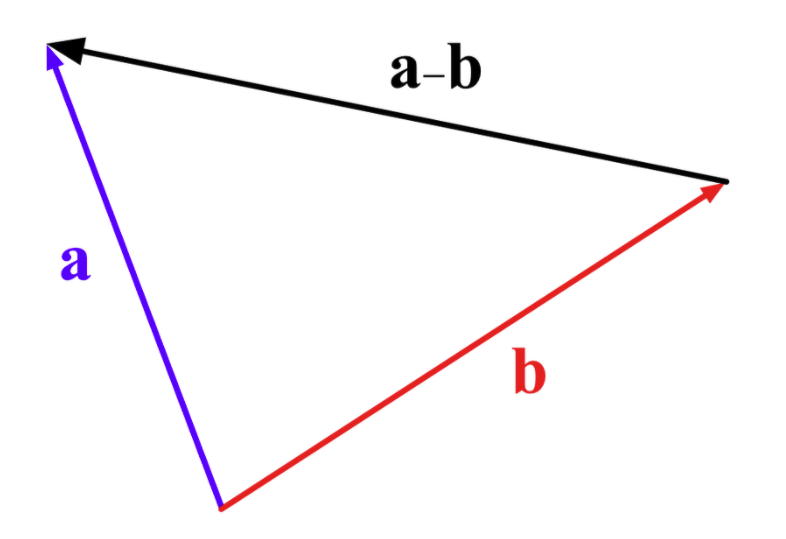
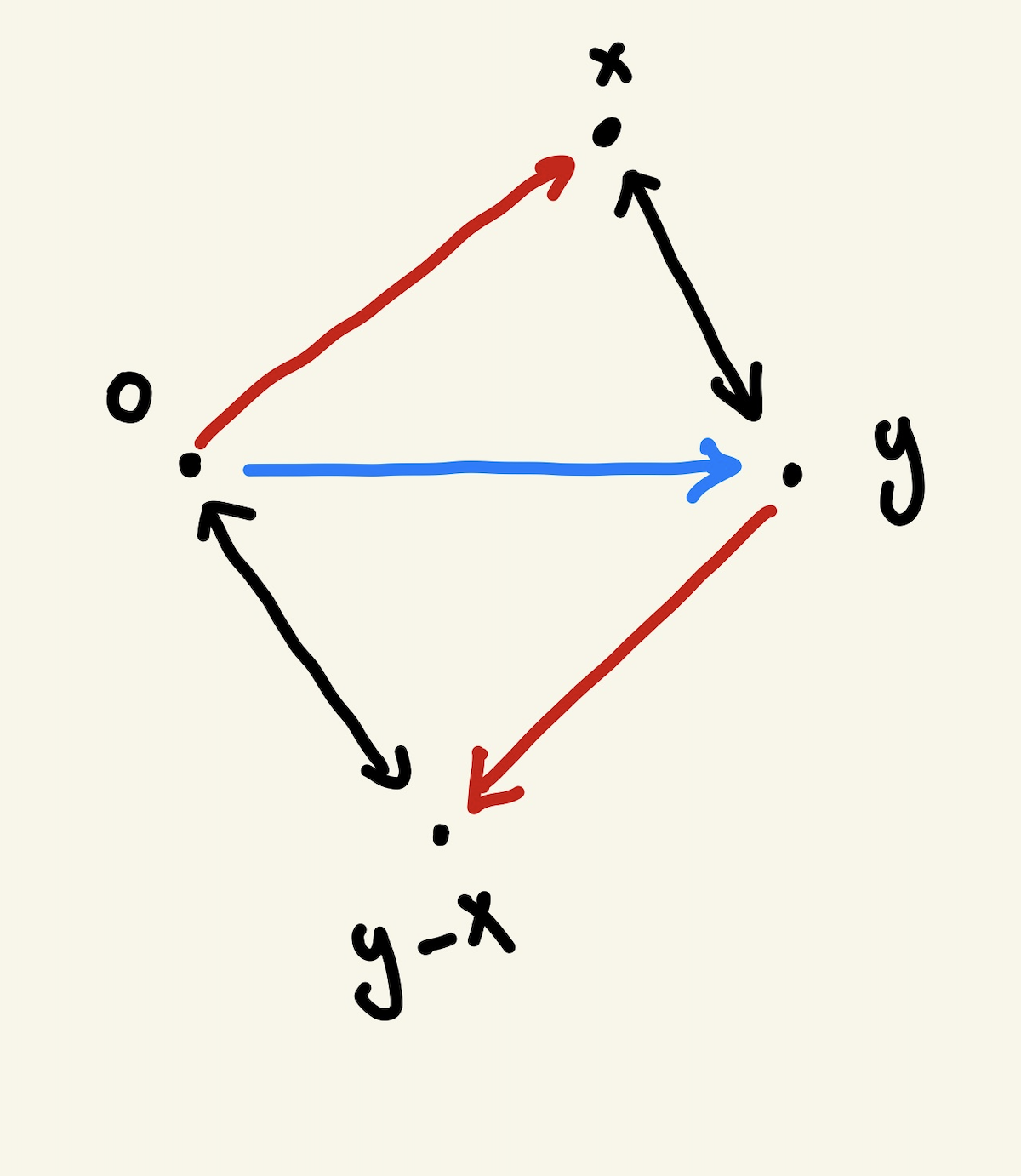
벡터의 뺄셈
빼는 벡터의 방향을 바꾸워 더한것과 같음
Norm
-
norm이란?
원점에서부터의 거리를 말함 -
L1-norm
각 성분의 변화량의 절대값을 모두 더함
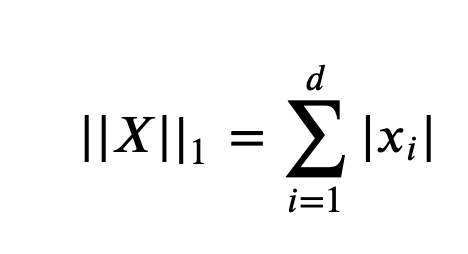
-
L2-norm
피타고라스 정리를 이용한 유클리드 거리를 말함
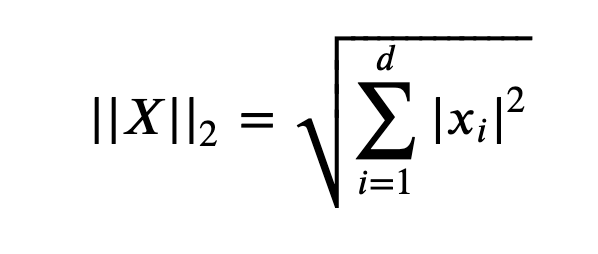
-
norm에 따라 기하학적으로 거리를 표현하는 것에 대해 차이가 발생
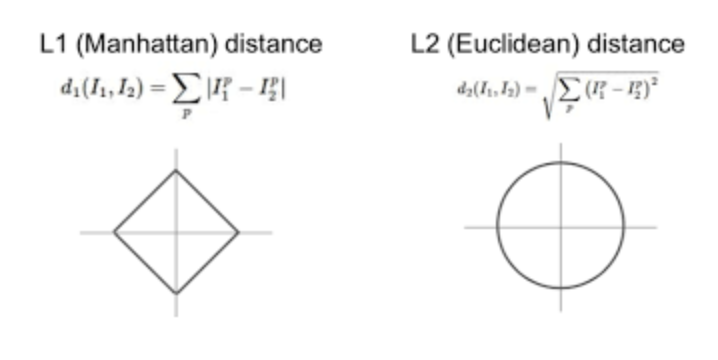
머신러닝 에서는 각각의 성질들이 필요할 때가 있으므로 둘 다 사용
구현 코드
def l1_norm(x):
x_norm = np.sum(np.abs(x))
return x_norm
def l2_norm(x):
x_norm = np.sqrt(np.sum(x*x))
return x_norm벡터 사이의 거리 및 각도
-
norm을 이용하여 두 벡터 사이의 거리를 계산 할 수 있다.
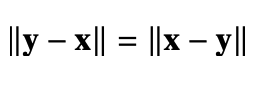
-
두 벡터 사이의 거리를 이용하여 각도계산이 가능하다!(단, L2-norm일때만 가능)
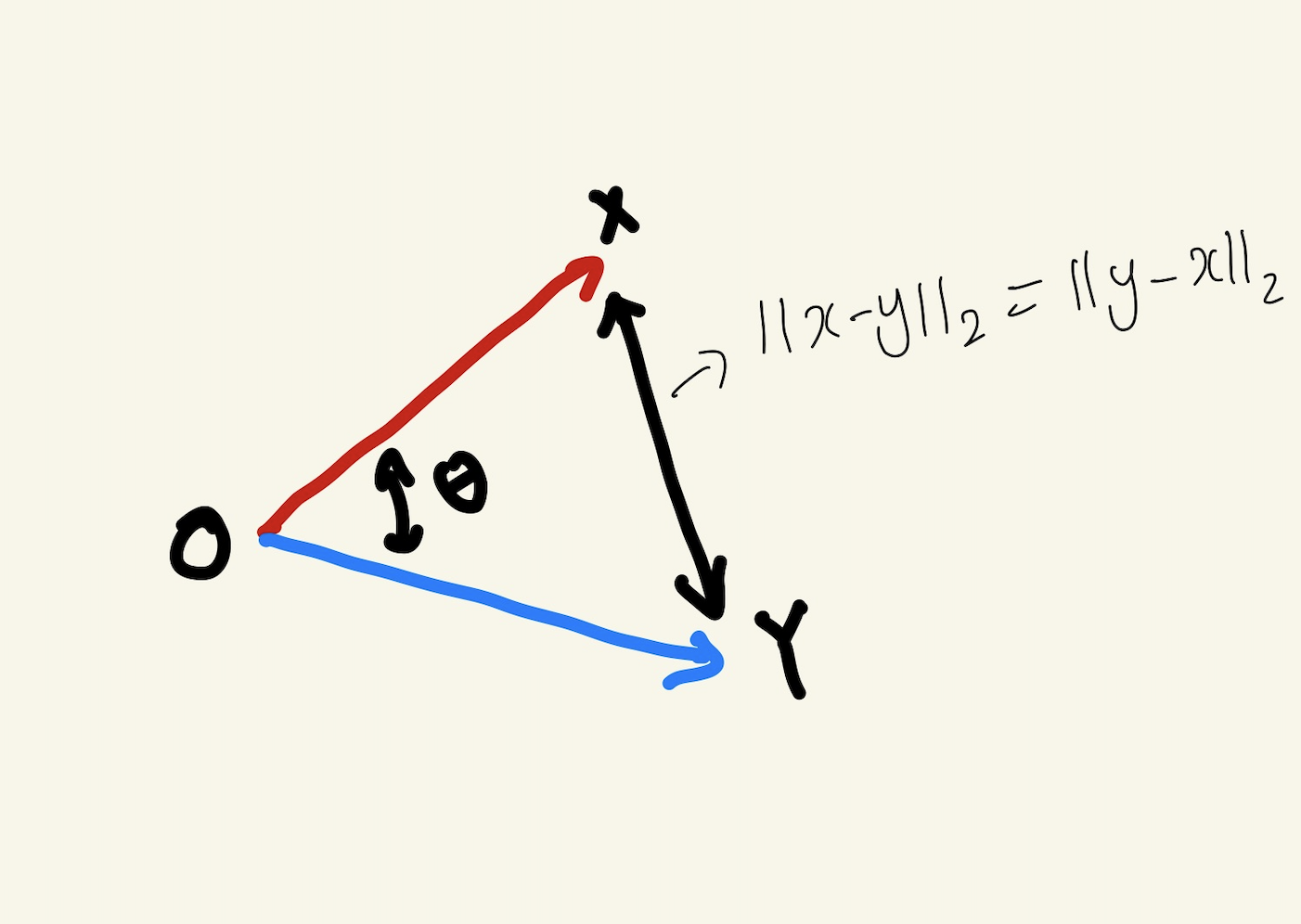
이때, 코싸인 제 2법칙에 의해 다음과 같은 등식이 성립
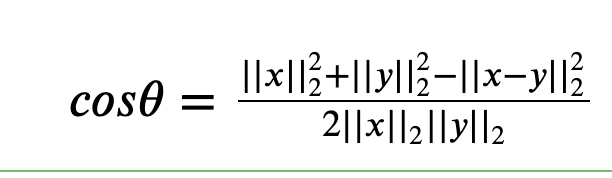
이때, 분자를 쉽계 계산하는 방법은 내적이므로 이를 내적을 이용하여 식을 정리하면 다음과 같다.(이때, <x,y>는 내적을 나타내고)


이때, <x,y>는 내적을 나타내고 내적 공식은 다음과 같다.
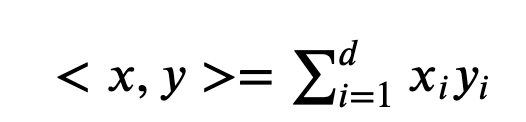
구현코드
#np.inner => 내적 계산
def angle(x,y):
v = np.inner(x,y) / (l2_norm(x) * l2_norm(y)) #코싸인의 값을 구함
theta = np.arccos(v) #코싸인의 역
return theta- 내적은 정사영된 벡터의 길이와 관련이 되어 있다.
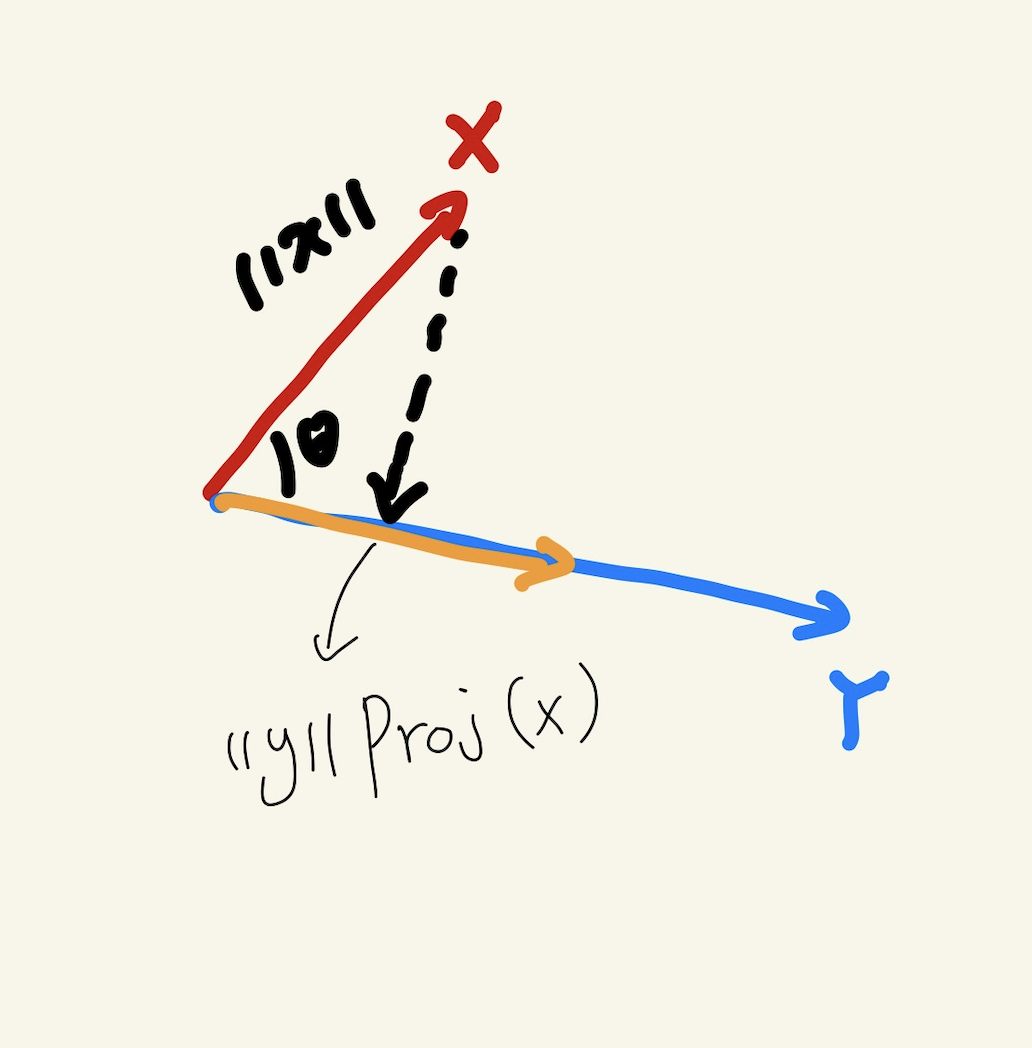
이때, Proj(x)길이는 코싸인 법칙에 의해 ||x||cos(Θ)가 되고 내적의 값은 다음과 같다.
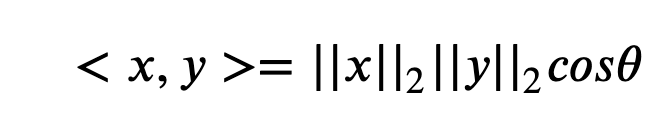
Reference
Naver BoostCamp AI Tech - edwith 강의
http://www.ktword.co.kr/abbr_view.php?m_temp1=3470
https://m.blog.naver.com/PostView.nhn?blogId=ruvendix&logNo=221192828884&proxyReferer=https:%2F%2Fwww.google.com%2F
https://junklee.tistory.com/29
