행렬

행렬

---

• 행렬이란?
  벡터를 원소로 가지는 2차원 배열
  

• 행렬의 특징

  • 행과 열로 이뤄져 있는 인덱스를 가지고 있다.
  • 행렬의 특정 행(열)을 고정하면 행(열)벡터라 한다.

• 전치행렬이란?
  기존의 행렬에서 행과 열의 바꾸워 표현한 행렬히다

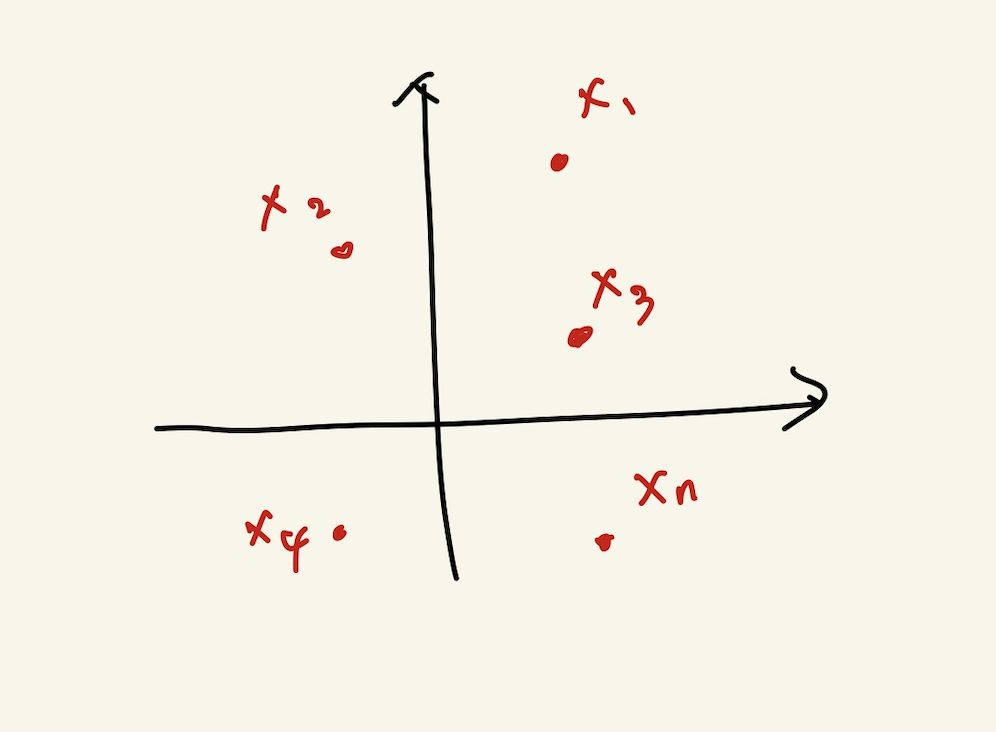
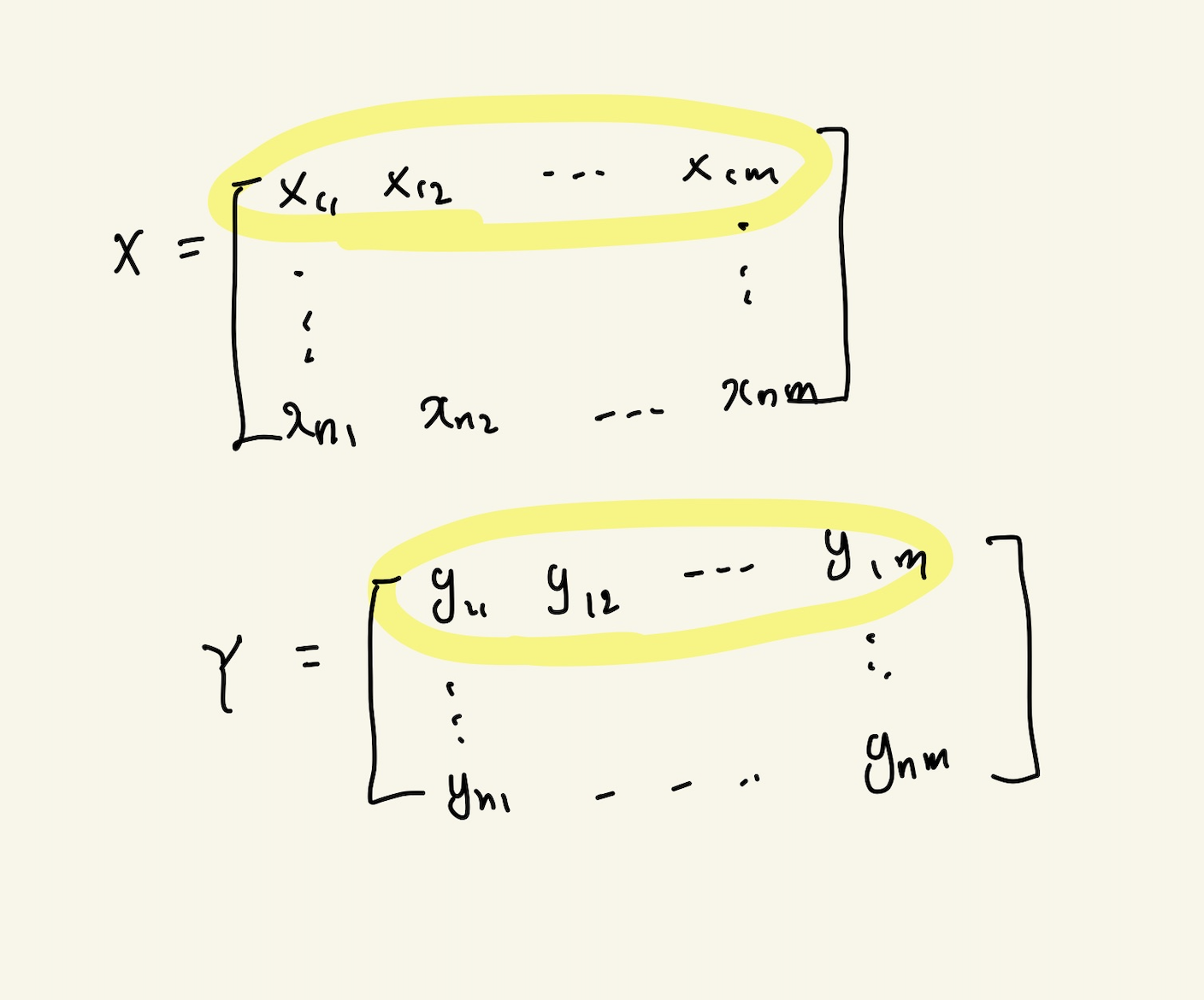
• 행렬은 여러 점들을 나타낸다.
  
  

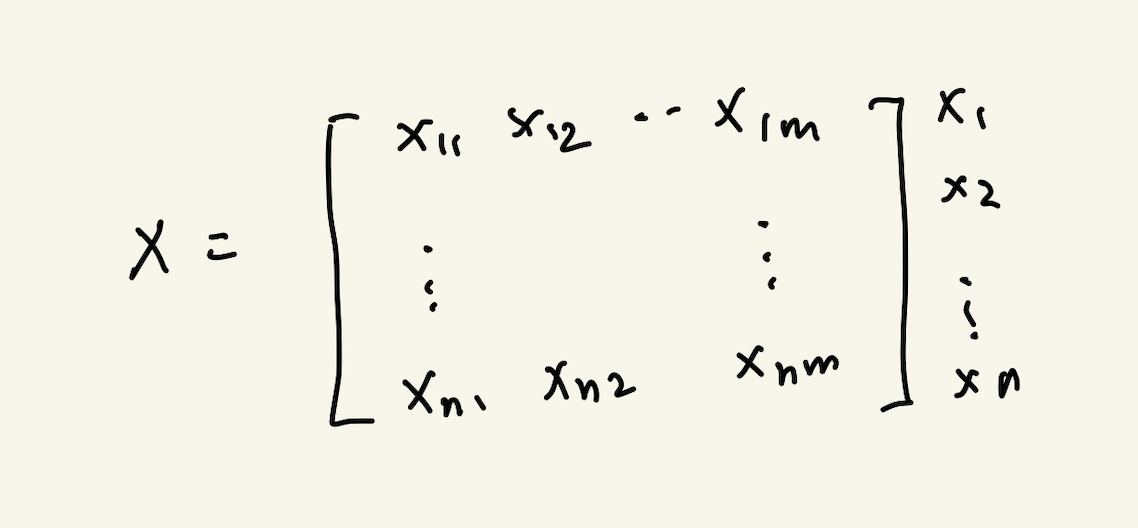
• 행렬끼리 같은 모양을 가지면 덧셈,뺄셈,성분곱을 계산 할 수 있다.

• 스칼라 곱도 마찬가지로 모든 원소에 스칼라 값을 곱해주면 된다.

• 행렬의 곱의 특징

  • A(3,2)행렬과 B(2,4)행렬을 곱한다면 <행렬(row수,column수)>
    • A의 열의수와 B의 행의수는 같아야 한다
    • 결과 행렬의 형태는 A의 행의수 * B의 열의수 형태로 반환이 된다.
    • 따라서, 이러한 특징으로 벡터를 다른 차원의 공간으로 보낼 수 있다.

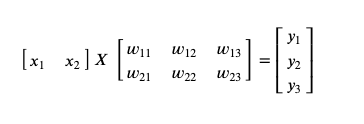
예시 코드

X = np.array([[1,2,3],
            [4,5,6],
            [7,8,9]])

Y = np.array([[0,1],
            [1,0],
            [1,1]])
            
print(X @ Y)

• inner사용 시 주의!
  i 번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬 계산
  수학에서는 아래와 같이 표현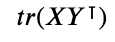

역행렬

---

• 어떤 행렬A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inversematrix)라고 한다.
• 역행렬을 구할 수 있는 조건
  • 행과 열의 수가 같아야 한다.
  • 행렬식(determinant)가 0이 되면 안된다.
• 
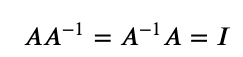
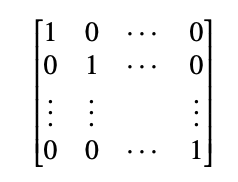
• 항등행렬 "I" 는 다음과 같은 형태이다.
  
• 역행렬을 구하는 코드

X = np.array([[1,1,1], [0,1,2], [1,1,0]])

print(np.linalg.inv(X))

• 역행렬을 구하기 위해서는 행과 열의 수가 같아야 하는 제약 조건등이 있으므로 역행렬을 수할 수 없다면 유사역행렬(pseudo-inverse)또는무어펜로즈(Moore-Penrose)역행렬을 사용다도록 한다.
  
  

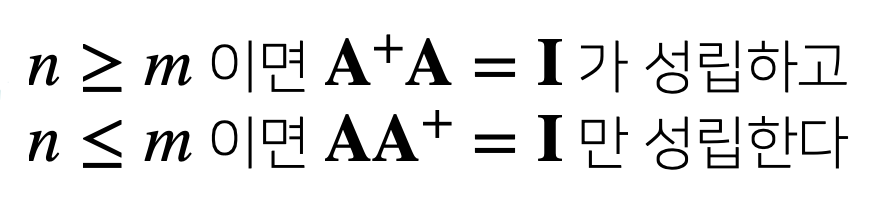
출처
Naver BoostCamp AI Tech - edwith 강의

• 유사역행렬 구하는 코드

Y = np.array([[0,1],
             [0,-1],
             [-2,0]])

np.linalg.pinv(Y)

np.linalg.pinv(Y) @ Y

Y = np.array([[0,1,2],
             [3,4,5]])
             
np.linalg.pinv(Y)

Y @ np.linalg.pinv(Y)

역행렬과는 다르게 기존 함수와 곱해줄 때 shape에 맞춰서 곱하여야 한다.
m이 큰 경우 유사역행렬을 먼저 곱하고 n이 큰 경우 유사역행렬을 나중에 곱해준다.

Reference

Naver BoostCamp AI Tech - edwith 강의
https://darkpgmr.tistory.com/104