확률론
- 확률론은 왜 필요할까?
- 기계학습에서 사용되는 손실함수(loss function)의 작동 원리는 데이터 공간을 통계적으로 해석하여 유도하게 된다.
- 손실함수 : 오차제곱합<L2- norm 사용>, 교차엔트로피 사용
- 분산 및 불확실성을 최소화하기 위해 측정하는 방법을 알아야 한다 - 확률론 기반
손실함수
- 손실함수란 신경망 성능의 나쁨을 나타내는 지표로써 학습의 기준으로써 사용이 된다.
- 왜 정확도를 지표로 삼지 않고 손실 함수를 지표로 삼는가?
- 정확도를 기준으로 지표를 삼으면 함수 자체가 이어져 있지 않은 계단함수로써 표현이 되기 때문에 학습이 잘 이뤄지지 않는다.
(가령, 100개의 데이터 셋이 존재하고 50개가 올바르게 인식이 된다면 정확도는 50%이고 값을 바꾸면 50.1%, 50.2%같은 정확도로 판단이 되어지지 않고 임계값을 기준으로 51%, 49%같은 정확도가 도출된다.)
따라서, 손실함수는 연속적인 변화를 나타낼 수 있음으로 손실함수로써 지표를 삼게 된다.
- 정확도를 기준으로 지표를 삼으면 함수 자체가 이어져 있지 않은 계단함수로써 표현이 되기 때문에 학습이 잘 이뤄지지 않는다.
- 손실함수의 종류는 오차제곱합, 교차 엔트로피 오차가 존재한다.
- 오차제곱합
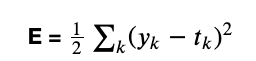
- y는 신경망의 출력값, t는 정답 레이블, k는 데이터의 차원 수
예측값과 실측값의 차이를 구하여 손실에 대한 정도를 구함 - W에 대한 2차원 함수로써 표현이 되고 그래프로써 W변수가 하나이고 W변수가 여러개면 그릇모양으로써 최소값이 하나가 되는형태이다.
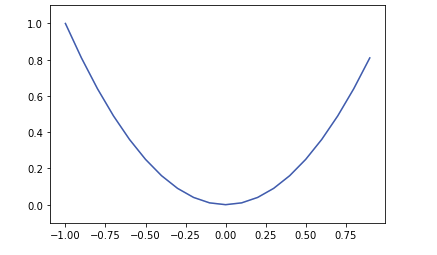
- y는 신경망의 출력값, t는 정답 레이블, k는 데이터의 차원 수
- 교차 엔트로피 오차
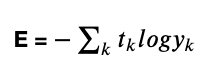
- y는 신경망의 출력값, t는 정답 레이블, k는 데이터의 차원 수
- 정답 레이블만 1이므로 정답 레이블에 대하여 확률의 log값을 판단한다
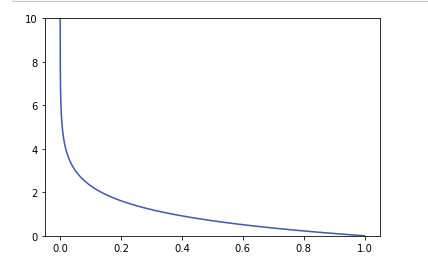
- -log그래프로써 1값에 가까울 수록 0값에 가까워 지는 것을 볼 수 있다 .
- 코드로써 구현을 할 때, y값에 0이 들어가게 되면 'inf'값 즉, 무한대 값이 나와 계산이 진행이 됨으로 y값에 아주 작은 수를 더하여(예: 1e-6의 수) 계산을 진행 하도록 한다.
- 미니배치 학습
방대한 학습 데이터를 전부 조사하여 일일히 손실함수를 게산하는 것은 현실적이지 않음으로 데이터 일부를 추려 전체의 근사치로 이용한다.(일부만 골라 학습을 수행)
- 오차제곱합
이산확률변수 & 연속확률변수
- 확률변수란?
어떤 시행의 결과에 따라 변수 X가 취할 수 있는 값과 그 확률이 각각 정해질때, 변수 X를 확률변수라 한다. - 이산확률변수란?
- 확률변수가 가질 수 있는 모든 경우의 수를 모두 고려하여 확률을 더하여 모델링(즉, 확률변수가 실수 전체의 범위가 아닌 정수 등 연속적이지 않은 값 - 주사위 굴리기..)
- 연속확률변수란?
- 데이터 공간에 정의된 확률변수의 밀도위에서의 적분을 통해 모델링한다.
(즉, 확률변수가 실수 전체의 범위 - 나이,몸무게...)
- 데이터 공간에 정의된 확률변수의 밀도위에서의 적분을 통해 모델링한다.
데이터의 초상화
-
결합확률분포란?
이산확률변수가 두개인 확률질량함수 -
데이터공간 x,y에에서 데이터공간에서 결합분포P(x,y)는 데이터 공간을 정의
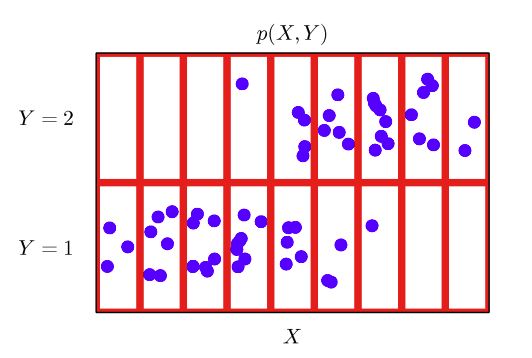
-
p(x)는 입력 x에 대한 주변확률분포이고 y의 정보를 포함하고 있지 않다.(x의 관점)
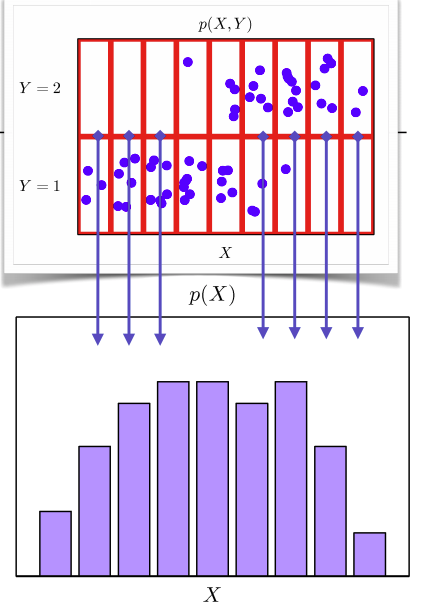
-
조건확률분포 P(x|y)는 데이터 공간에서 x,y의 관계를 표현한다.
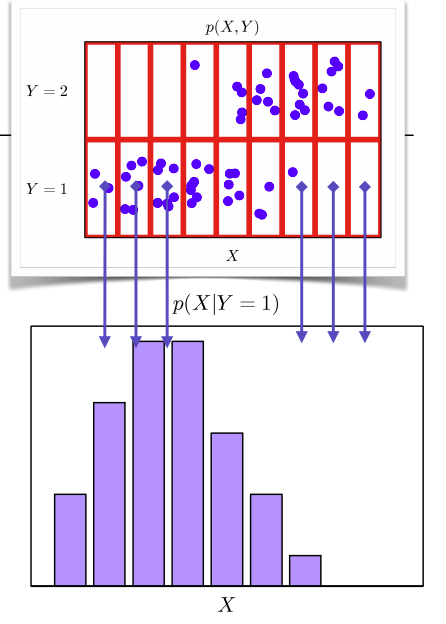
출처
Pattern Recognition and Machine Learning, Bishop
기대값,분산,첨도,공분산
- 기대값 : 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값
- 이산확률변수
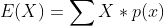
- 연속확률변수

- 이산확률변수
- 분산 : 확률변수가 기댓값으로부터 얼마나 떨어진 곳에 분포하는지를 가늠하는 수(클수록 넓게 퍼져 있다)
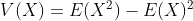
- 첨도(Kurtosis): 확률분포의 뾰족한 정도를 나타내는 척도(정규분포의 첨도는 0- 기본 정의에 의하면 3이나 보통 0으로 만들어주고 다시 정의, 이를 excess Kurtosis라 한다, 0인 첨도를 가지는 경우를 Mesokurtic이라 한다, 0보다 작으면 정규분포보다 납작한 모양, 0보다 큰 경우 정규분포보다 뾰족한 모양이다.)
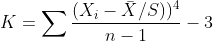
(이때, Xhat은 표본평균, s 는 표본표준편차이다.) - 공분산: 두 확률변수 X, Y의 상관관계를 나타내는 척도이다.
값이 0보다 크면 X증가 - Y증가/값이 0보다 크면 X증가 - Y감소/값이0이면 두 변수간에 아무런 선형관계가 없다.
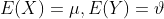

즉, 공분산은 X의 편차와 Y의 편차를 곱한것의 평균이다.
몬테카를로 샘플링
- 몬테카를로 방법이란?
시뮬레이션 테크닉의 일종으로, 구하고자 하는 수치의 확률적 분포를 반복 가능 한 실험의 통계로부터 구함
=> 이를 이용하여 임의의 구역의 난수의 점을 찍고 함수로 둘러쌓인 공간의 크기를 구할 수 있다. - 몬테카를로 방법을 이용한 원주율 구하기
원의 넓이 공식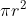
이때, 원주율을 구하기 위해서는 원의 넓이, 반지름의 길이를 알면 구할 수 있는데 원의 몬테카를로 방법을 이용하여 원의 넓이를 구함으로써 이를 해결 할 수 있다.
import math
total = 100000
radius = 1
# low값은 포함, high값은 포함되지 않음
x = np.random.uniform(low = 0, high = 1, size = total)
y = np.random.uniform(low = 0, high = 1, size = total)
dist = np.sqrt(x**2 + y**2)
n = sum(dist < radius) #거리 < 반지름인 점
print(n / total) #추정한 원의 넓이
print(math.pi / 4) #실제 원의 넓이-
몬테카를로 방법을 이용하여 기대값을 구할 수 있는데 이는 다음과 같은 식이 성립한다.
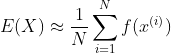
- 반복적으로 어떠한 값이 나오는지 구하여 그것의 평균을 내어준다.
- 몬테카를로는 이산형이든 연속형이든 상관없이 성립한다.
-
몬테카를로 방법을 이용하여 기대값을 구하여 어려운 적분값을 도출 할 수 있다.
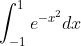
해당 식은 가우시안 함수로써 적분하기 어려운 함수이다.
따라서, 직접적으로 적분을 하지 않고 기댓값으로 넓이를 대략적으로 구할 수 있는데 기댓값의 공식은 다음과 같다.

해당 식이 의미하는바를 그래프로 그려보게 되면 다음과 같다.

이를 이용하여 수식을 도출해 보게 된다면 다음과 같다.
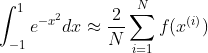
위와 같은 방식으로 적분의 값을 쉽게 구할 수 있다.
import numpy as np
def gaussian_fun(x):
return np.exp(-x ** 2)
class MonteCarloTestPerformer:
def __init__(self):
self.repeat = 100000 # 반복 연산 횟수 지정
# 범위는 -1 부터 1사이의 값으로 고정
def solution1(self):
cnt = 0
for i in range(self.repeat): # 점을 무작정 다 찍어주는 방법 (0 ~ 1사이)
x = gaussian_fun(np.random.uniform(0, 1))
y = np.random.uniform(0, 1)
if x - y >= 0:
cnt += 1
print((cnt / 100000) * 2)
# 범위는 -1 부터 1사이의 값으로 고정
def solution2(self):
low = -1
high = 1
int_len = np.abs(high - low) # 범위를 고려한 구현
stat = []
for _ in range(self.repeat):
x = np.random.uniform(low=low, high=high, size=1)
stat.append(gaussian_fun(x))
print(np.mean(stat) * int_len)
if __name__ == '__main__':
performer = MonteCarloTestPerformer()
performer.solution1()
performer.solution2()출처
Naver BoostCamp AI Tech - edwith 강의
Reference
Naver BoostCamp AI Tech - edwith 강의
https://bskyvision.com/455
http://blog.naver.com/PostView.nhn?blogId=mykepzzang&logNo=220836609004
https://datacookbook.kr/59
https://ko.wikipedia.org/wiki/%EB%B6%84%EC%82%B0
https://m.blog.naver.com/PostView.nhn?blogId=s2ak74&logNo=220616766539&proxyReferer=https:%2F%2Fwww.google.com%2F
https://m.blog.naver.com/PostView.nhn?blogId=chochila&logNo=40144022678&proxyReferer=https:%2F%2Fwww.google.com%2F
https://destrudo.tistory.com/15
https://m.blog.naver.com/PostView.nhn?blogId=keebh&logNo=20115141888&proxyReferer=https:%2F%2Fwww.google.com%2F
