그래프
.png)
- 그래프(Graph)는 정점 집합과 간선 집합으로 이루워진 수학적 구조
- 간선은 두 개의 정점을 연결하고 모든 정점이 간선으로 직접적으로 연결되어 있지 않을 수 있다.
- 그래프는 네트워크(Network)로도 불리운다.
- 정점(Vertex)은 노드(Node), 간선은 엣지(Edge)또는 링크(Link)
라고 불리운다. - 그래프는 복잡계(Complex System)를 표현하고 분석하기 위한 언어이다.
- 복잡계는 뇌(뉴런 간 연결), 지식 그래프, 화학 분자, 단백질 상호작용, 세포간 유사도 그래프, 이미지 분해 등의 분야가 존재한다.
- 그래프의 유형
1, Undirect Graph VS Direct Graph

Undirect Graph : 방향이 없는 그래프
.png)
Direct Graph : 방향이 있는 그래프
2, Unweighted Graph VS Weight Graph

Unweighted Graph : 가중치가 없는 그래프
.png)
Weighted Graph : 가중치가 있는 그래프
3, Unpartite Graph VS Bipartite Graph

Unpartite Graph : 동종 그래프
✔️ 동종 그래프는 단일 종류의 정점을 가짐
✔️ 웹 그래프, 소셜 네트워크의 친구 그래프등이 이에 해당한다.
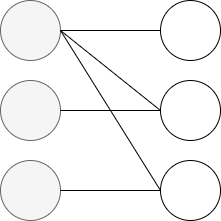
Bipartite Graph : 이종 그래프
✔️ 다른 종류의 정점사이에만 간선이 연결됨
✔️ 전자 상거래 구매내역(사용자, 상품), 학교(학생과 선생님)그래프 등이 이에 해당한다.
-
그래프의 표기법
정점들의 집합을 , 간선들의 집합을, 그래프를 로 표현한다. -
정점의 이웃(Neighbor)
정점의 이웃이란 정점과 연결된 다른 정점을 의미한다.
✔️ 정점 의 이웃들의 집합을 또는 등의 표기로 표기한다.
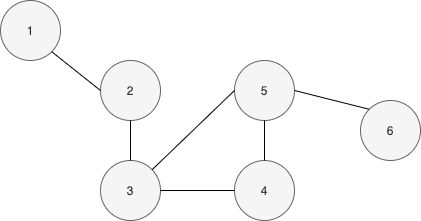
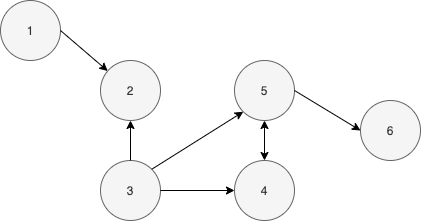
✔️ 방향성이 있는 그래프에서는 나가는 이웃들과 들어오는 이웃을 구분한다.
✔️ 정점 에서 간선이 나가는 이웃(Out- Neighbor)의 집합을 보통 로 표시하고 들어오는 이웃(In-Neighbor)의 집합을 보통 로 표시한다.
-
그래프의 종류와 유형
-
간선 리스트(Edge list) : 그래프를 간선들의 리스트로 저장, 각 간선은 해당 간선이 연결하는 주 정점들의 순서쌍(pair)으로 저장(방향성이 있는 경우 (출발점, 도착점)순서로 저장)
-
인접 리스트(Adjacent list) : 각 정점의 이웃들을 리스트로 저장(방향성이 있는 경우 나가는 이웃들과 들어오는 이웃들을 각각 리스트로 저장)
-
인접 행렬 : 2차원 배열을 통해 저장
- 일반 행렬 : 전체연결 경우의 수를 고려하여 저장
- 희소 행렬 : 0이 아닌 원소만을 저장(간선의 수에 비례하는 저장 공간을 사용)
예시) 3번노드 2번노드 가중치 2인 간선, 2번노드 4번노드에 가중치 3인 간선
3 2 2
2 4 3
이러한 형태의 2차원 배열로 저장
-
#networkx 라이브러리 예시
import networkx as nx
G = nx.Graph()
ListGraph = nx.to_dict_of_lists(G) # 인접 리스트
EdgeListGraph = nx.to_edgelist(G) # 간선 리스트
NumpyArrayGraph = nx.to_numpy_array(G) # 인접 행렬(일반 행렬)
SparseMatrixGraph = nx.to_scipy_sparse_matrix(G) # 인접 행렬(희소 행렬) 실제 그래프 VS 랜덤 그래프
- 랜덤 그래프란?
랜덤 그래프란 확률적으로 간선을 부여하여 만든 그래프를 말한다.
랜덤 그래프를 만드는 여러 프로세스들이 존재하는데 그 중 에어디쉬-레니 랜덤 그래프(Erdős-Rényi Random Graph)가 존재한다. 에어디쉬-레니 랜덤 그래프는 (Erdős-Rényi Random Graph)
임의의 두 정점 사이에 간선이 존재하는지의 여부는 동일한 확률분포에 의해 결정되는 그래프이다.
에어디쉬-레니 랜덤 그래프는 로써 표현이 되어지고 다음과 같은 특징을 가진다.
✔️ 은 정점의 수를 나타낸다.
✔️ 임의의 두 개의 정점 사이에 간선이 존재할 확률은 이다.
✔️ 정점 사아의 연결은 서로 독립적(Independent)이다.
예시) 에어디쉬-레니 랜덤 그래프 에 의해 생성될 수 있는 그래프와 각각의 확률은?
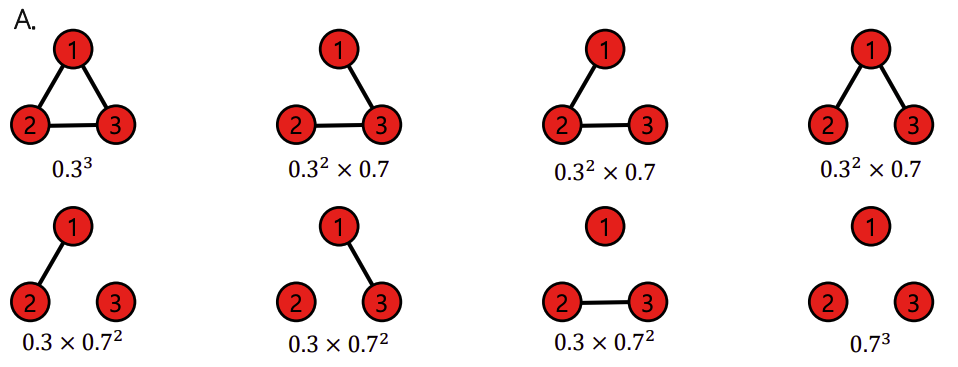
출처: Naver BoostCamp AI Tech - edwith 강의
작은 세상 효과
-
경로(path)
정점 와 의 사이의 경로(path)는 다음과 같은 조건을 만족하는 정점들의 순열(Sequence)이다.
✔️ 에서 시작해서 에서 끝나야 한다.
✔️ 순열에서 연속된 정점은 간선으로 연결되어 있어야 한다. -
길이
경로의 길이는 해당 경로 상에 놓이는 간선의 수로 정의 -
거리(Distance)
정점 와 의 사이의 거리(Distance)는 와 사이의 최단 경로의 길이이다. -
지름(Diameter)
그래프의 지름(Diameter)은 정점 쌍의 거리 간 최댓값이다.
def getGraphDiameter(Graph):
diameter = 0
for v in Graph.nodes:
length = nx.single_source_shortest_path_length(Graph, v)
max_length = max(length.values())
if max_length > diameter:
diameter = max_length
return diameter-
작은 세상 효과란 무었일까?
어떠한 관계에 있어 몇 단계만 거치면 서로 연결되어 있다는 이론이다.
실제 예시로는 여섯 단계 분리(Six Degrees of Separataion) 실험, MSN메신저를 예시로 들 수 있다.
✔️ 작은 세상 효과는 실생활을 표현한 그래프에서는 물론 높은 확률로 랜덤 그래프에도 존재한다. -
특정한 그래프(체인(Chain), 사이클(Cycle), 격자(Grid) 그래프)에서는 작은 세상 효과가 존재하지 않는다.
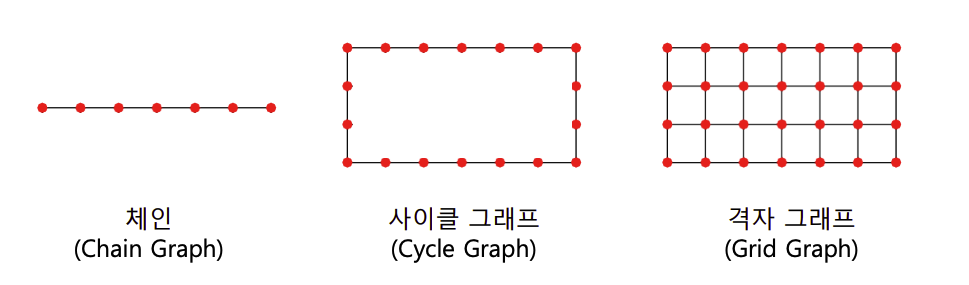
출처: Naver BoostCamp AI Tech - edwith 강의
연결성의 두터운-꼬리 분포
-
연결성(Degree)
정점의 연결성(Degree)은 그 정점과 연결된 간선의 수를 의미한다.
✔️ 정점 의 연결성은 해당 정점의 이웃들의 수와 같고 표기는 , , 같은 표기법으로 표현한다.

✔️ 방향성이 있는 그래프에서는 나가는 연결성(Degree)과 들어오는 연결성(Degree)을 구분한다.
✔️ 정점 v에서 나가는 연결성(Out Degree)은 에서 나가는 간선의 수를 의미하며 혹은 로 표시하며 들어오는 연결성(In Degree)은 들어오는 간선의 수를 의미하며 혹은 으로 표시한다.

-
실제 그래프의 연결성 분포는 두터운 꼬리(Heavy Tail)를 가지나 랜덤 그래프의 연결성 분포는 높은 확률로 정규 분포와 유사하다.
(이때, 연결성이 매우 높은 정점은 허브(Hub)정점이라 하며 랜덤 그래프는 허브 정점이 존재할 가능성이 0에 가깝다.)
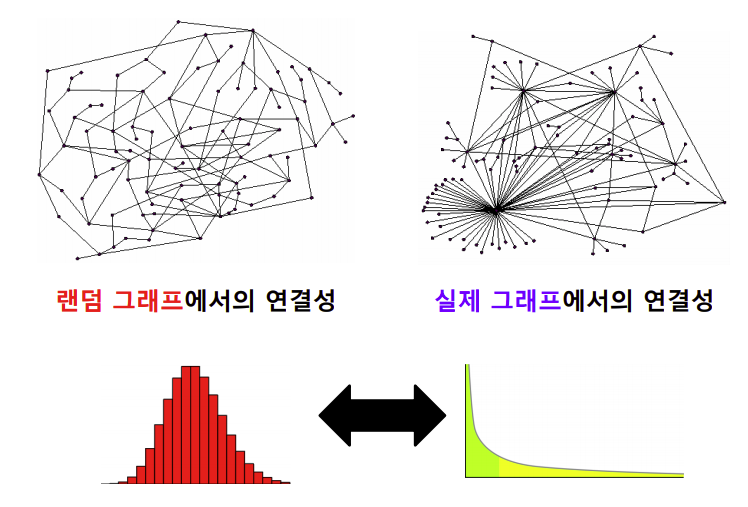
출처: Naver BoostCamp AI Tech - edwith 강의
(두터운 꼬리 예시 => 인스타그램의 팔로워 수는 극단적으로 많은 사람은 드물다.)
거대 연결 요소
-
연결 요소(Connected Component)
연결요소(Connected Component)는 다음과 같은 정점들의 집합을 의미한다.
✔️ 연결 요소에 속하는 정점들은 경로로 연결될 수 없다.
✔️ 위의 조건을 만족하며 정점을 추가 할 수 없다.
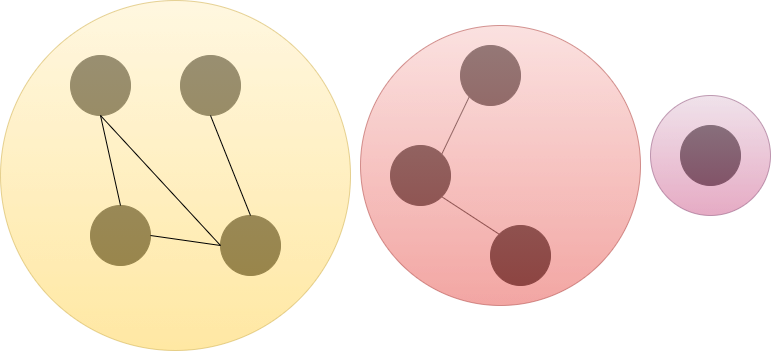
-
실제 그래프에서는 거대 연결 요소(Giant Connected Component)가 존재한다.(거대 연결 요소는 대다수의 정점을 포함)
예시) 어느 메신저 그래프는 99.9%의 정점이 하나의 거대 연결 요소에 포함
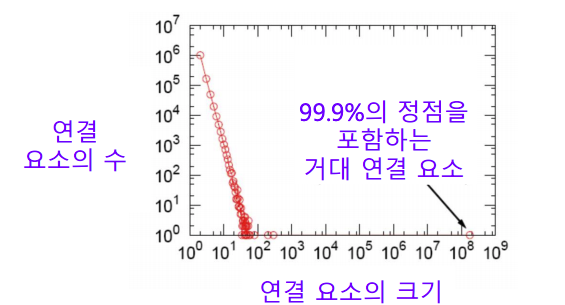
출처: Naver BoostCamp AI Tech - edwith 강의 -
랜덤 그래프는 높은 확률로 거대 연결 요소(Giant Connected Component)가 존재한다.
이때, 정점들의 평균 연결성이 1 보다 충분히 커야 한다.
직관적으로 생각 해 보면 간선이 하나 있어야 연결요소가 생기는데 은 을 간선의 수로 본다면 간선이 생기는 수로 써 볼 수 있다. 따라서, 이 값이 1이 넘어야 급격하게 연결 요소가 생긴다고 생각 할 수 있다.
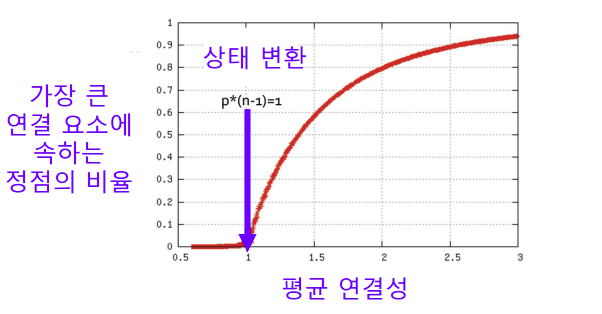
출처: Naver BoostCamp AI Tech - edwith 강의
참고 : https://brianzhang01.github.io/2018/07/random-graphs-and-giant-components/
군집 구조
-
군집(Community)
군집(Community)이란 다음 조건들을 만족하는 정점들의 집합이다.
✔️ 집합에 속하는 정점 사이에는 많은 간선이 존재
✔️ 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재 -
지역적 군집 계수(Local Clustering Coefficient)
지역적 군집 계수(Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 측정한다.
정점 의 지역적 군집 계수는 정점 의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 말한다.
정점 의 지역적 군집 계수를 로 표현 할 시 예시는 다음과 같다.
예시)
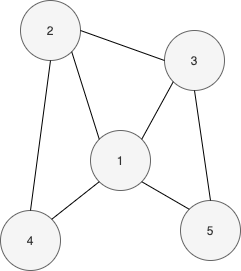
정점 1의 이웃은 4개(2,3,4,5)이며, 총 6개의 이웃 쌍<이웃으로 만들어 낼 수 있는 쌍>(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)이 존재하고 그 중 3개의 쌍이 간선으로 직접 연결되어(2,3),(2,4),(3,5) 있어 군집계수 는 이다.
(이때, 연결성이 0인 정점에서는 지역적 군집 계수가 정의되지 않는다.)
지역접 군집 계수가 군집이랑 어떻게 연관이 있는 것인가?
✔️ 정점의 지역적 군집 계수가 매우 높으면 이웃들고 높은 확률로 서로 간선으로 연결되어 있고 정점와 그 이웃들은 높은 확률로 군집을 형성한다. -
전역 군집 계수(Global Clustering Coefficent)
전역 군집 계수(Global Clustering Coefficent)는 전체 그래프에서 군집의 형성 정도를 측정한다.
그래프의 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균이다.(정의되지 않는 정점은 제외)
def getGraphAverageClusteringCoefficient(Graph):
ccs = []
for v in Graph.nodes:
num_connected_pairs = 0
for neighbor1 in Graph.neighbors(v):
for neighbor2 in Graph.neighbors(v):
if neighbor1 <= neighbor2:
continue
if Graph.has_edge(neighbor1, neighbor2):
num_connected_pairs += 1
cc = num_connected_pairs / (Graph.degree(v) * (Graph.degree(v) - 1) / 2) # 분모 - Combination개념을 이용(v에 연결된 정점들 중 2개를 고름)
ccs.append(cc)
return sum(ccs) / len(ccs)- 실제 그래프에서의 군집 계수가 높은 이유
✔️ 동질성 : 서로 유사한 정점끼리 간선으로 연결될 가능성이 높음
✔️ 전이성 : 공통 이웃이 있는 경우, 공통 이웃이 매개 역활을 해줄 수 있음
❗️ 반면 랜덤 그래프에서는 지역적 혹은 전역 군집 계수가 높지 않다.(간선 연결이 독립적이기 때문 - 공통 이웃의 존재 여부가 간선 연결 확률에 영향을 미치지 않음)
그래프의 비교 분석
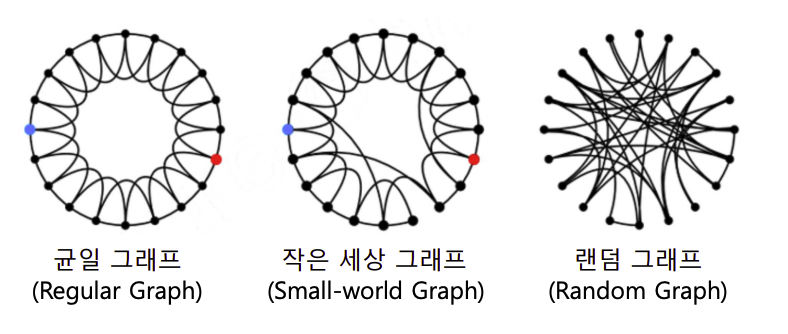
출처: Naver BoostCamp AI Tech - edwith 강의
균일 그래프 : 군집계수 - 크다, 지름 - 크다
작은 세상 그래프 : 군집계수 - 크다, 지름 - 작다
랜덤 그래프 : 군집계수 - 작다, 지름 - 작다
Reference
Naver BoostCamp AI Tech - edwith
https://brianzhang01.github.io/2018/07/random-graphs-and-giant-components/
