페이지랭크

페이지랭크의 배경

---

• 웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성이 있는 그래프
  
  ✔️ 웹페이지 : 정점
  
  ✔️ 웹페이지의 하이퍼링크 : 간선
  
  ❗️ 웹페이지는 추가적으로 키워드 정보를 포함하고 있음
  
  

• 첫번째 시도 : 웹을 거대한 디렉토리로 정리하는 것
  
  ✔️ 카테고리의 수와 깊이가 무한정 커지는 문제(웹페이지 수가 증가함에 따라)
  
  ✔️ 카테고리의 구분이 모호한 경우가 많아 저장과 검색에 어려움이 있음
  

• 두번째 시도 : 웹페이지에 포함괸 키워드에 의존한 검색엔진
  
  ✔️ 사용자가 입력한 키워드에 대해, 해당 키워드를 많이 포함한 웹페이지 반환
  
  ✔️ 악의적인 웹 페이지에 취약(악의적인 페이지에 연관없는 평범한 키워드를 여러번 넣어 유입을 유도)
  

⭐️ 사용자의 키워드와 관연성이 높고 신뢰 할 수 있는 웹페이지를 찾기 위하야 페이지랭크의 개념이 나오게 되었다.

페이지랭크의 정의

---

• 투표 관점에서의 페이지랭크
  
  ✔️ 투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾음
  
  ✔️ 투표의 주체 - 웹페이지/ 하이퍼링크 - 투표
  
  ✔️ 특정 웹페이지 $u$가 $v$로의 하이퍼링크를 포함하면 $u$의 작성자가 판단하기에 $v$가 관련성과 신뢰성이 있다고 보장해 주는 효과가 있다.
  ➡️ 예시 - 논문을 고를 때 많이 인용된 논문을 더 활용
  
  ✔️ 들어오는 간선의 수만 센다고 하여 신뢰할 수 있다는 보장을 할 수는 없다.(웹페이지를 여러개 만들어서 간선의 수를 부풀리는 악용 사례가 있을 수 있다.)
  
  ❗️ 이러한 악용 사례를 해결하기 위해 페이지랭크에서는 가중 투표를 하게 된다.(관련성이 높고 신뢰할 수 있는 웹사이트의 투표를 더 중요하게 간주, 그렇지 않은 웹사이트들의 투표는 덜 중요하게 간주 - 악용이 있어도 방어할 수 있는 합리적인 투표 방법)
  
  ⭐️ 이때, 신뢰성은 투표를 통해 측정을 하게 되는데 투표를 하지도 않았는데 어떻게 신뢰성이 있는가? => 재귀적인 방법 풀이로 인해 가능(코드구현 - 각 정점마다 동일한 신뢰성 세팅 후 재귀적으로 투표에 대한 연산을 수행하여 각 정점마다의 신뢰도가 수렴할때까지 작업을 수행)
  
  ✔️ 측정하여는 웹페이지의 관련성 및 신뢰도를 페이지랭크 점수라도 한다.
  이때, 각 웹페이지의 페이지랭크 점수는 받은 투표의 가중치 합으로 정의된다.
  예시)
  
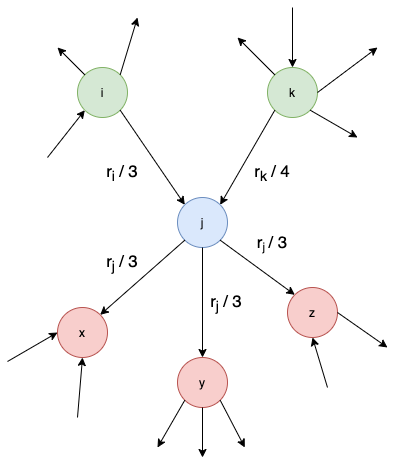
  이때, 웹페이지 $j$의 페이지랭크 점수 $r_j$는 다음과 같다.
  ➡️ $r_j = r_i/3 + r_k/4$
  
  페이지랭크 점수의 정의는 다음과 같다.
  ➡️ $r_j = \sum_{i \in N_{in}(j)}\frac{r_i}{d_{out}(i)}$
  
  ⭐️또한, 변수만큼 식이 존재함으로 연립방정식을 통하여 페이지 랭크 값을 구할 수 있고 이를 컴퓨터로 재귀(Recursion)의 방법으로 구하게 된다.
  
  $r_y = r_y/2 + r_a /2$
  $r_a = r_y + r_m$
  $r_m = r_a/2$
  
  
• 임의 보행 관점에서의 페이지랭크
  
  ✔️ 임의 보행을 통해 웹을 서핑하는 웹서퍼가 있다고 가정하였을 시 웹 서퍼는 연재 웹 페이지에 있는 하이퍼링크 중 하나를 균일한 확률로 클릭하는 방식으로 웹을 서핑하고 t번째 방문한 웹페이지가 웹페이지 $i$일 확률을 $p_i(t)$라고 하였을 때 $p(t)$는 길이가 웹페이지 수와 같은 확률분포가 되고 $t+1$번째의 $j$정점에서의 확률은 다음과 같다.
  $p_j(t+1) = \sum_{i \in N_{in}(j)}\frac{p_i(t)}{d_{out}(i)}$
  
  ➡️이때, 이 과정을 무한히 반복하면(t가 무한히 커지면), 확률 분포 $p(t)$는 수렴하게 된다. 즉, $p(t) = p(t+1) = p$가 성립하게 되고 수렴한 확률 분포 $p$는 정상 분포(Stationary Distribution)라고 부르게 된다.
  이에 따라 위의 식을 다음과 같이 바꿀 수 있다.
  $p_j = \sum_{i \in N_{in}(j)}\frac{p_i}{d_{out}(i)}$
  
  ⭐️ 이때, 투표 관점에서의 정의한 페이지랭크 점수는 임의 보행 관점에서의
  정상 분포와 동일하다.
  ➡️ $r_j = \sum_{i \in N_{in}(j)}\frac{r_i}{d_{out}(i)}$
  
  ➡️$p_j = \sum_{i \in N_{in}(j)}\frac{p_i}{d_{out}(i)}$
  

페이지랭크의 계산

---

• 페이지랭크 점수 계산은 반복곱(Power Iteration)을 사용한다.
  총 3단계로써 구성이 되어진다.
  
  ✔️ 각 웹페이지 $i$의 페이지랭크 점수 $r_i^{(0)}$를 동일하게 $\frac{1}{웹페이지의 수}$로 초기화
  
  ✔️ 아래의 식을 이용하여 각 웹페이지의 페이지랭크 점수를 갱신
  ➡️ $r_i^{(t+1)} = \sum_{i \in N_{in}(j)}\frac{r_i^{(t)}}{d_{out}(i)}$
  
  ✔️ 페이지랭크 점수가 수렴할때까지 페이지랭크 점수를 갱신
  
  ❗️위의 방법으로 반복곱이 항상 수렴하는지, 합리적인 점수로 수렴을 하지않는 경우가 존재 할 수 있다.
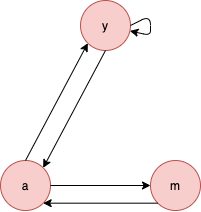
  ➡️ 스파이더 트랩(Spider Trap)
  들어오는 간선은 있지만 나가는 간선은 없는 정점집합이 있는 경우를 지칭하고 페이지랭크 점수가 수렴하지 않는 상황이 생긴다.
  
  b,c 정점이 해당
  
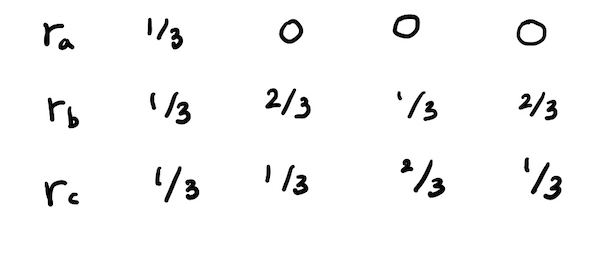
  ➡️ 막다른 정점(Dead End)
  들어오는 간선은 있지만 나가는 간선은 없는 경우를 지칭하고 페이지랭크 점수가 0으로 수렴하는 경우가 생긴다.
  
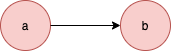
  b 정점이 해당
  
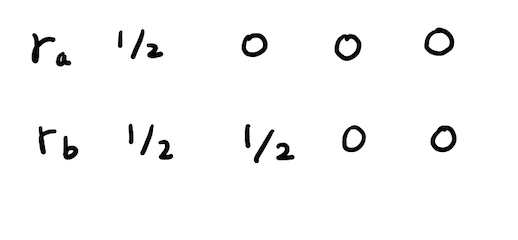
  ⭐️ 이러한 문제를 해결하기 위해 순간이동(Teleport)방법이 존재한다.
  ➡️ 감폭 비율(Damping Factor)을 통해 감폭비율에 속하면 하이퍼링트 중 하나를 균일한 확률로 선택하고 속하지 않으면 웹페지이로 순간이동한다.(보통 감폭비열은 0.8정도를 사용한다.)
  
  순간이동의 계산의 진행 방식
  
  ✔️ 각 막다른 정점에서(자신을 포함) 모든 다른 정점으로 가는 간선을 추가.
  
  ✔️ 아래 수식을 사용하여 반복곱을 수행
  $r_j = \sum_{i \in N_{in}(j)}(\alpha\frac{r_i}{d_{out}(i)}) + (1- \alpha)\frac{1}{|V|}$
  
  👉 $|V|$는 전체 웹페이지의 수
  
  👉 $\sum_{i \in N_{in}(j)}(\alpha\frac{r_i}{d_{out}(i)})$는 하이퍼링크를 따라 정점 $j$에 도착할 확률
  
  👉$(1- \alpha)\frac{1}{|V|}$는 순간이동을 통해 정점 $j$에 도착할 확률
  

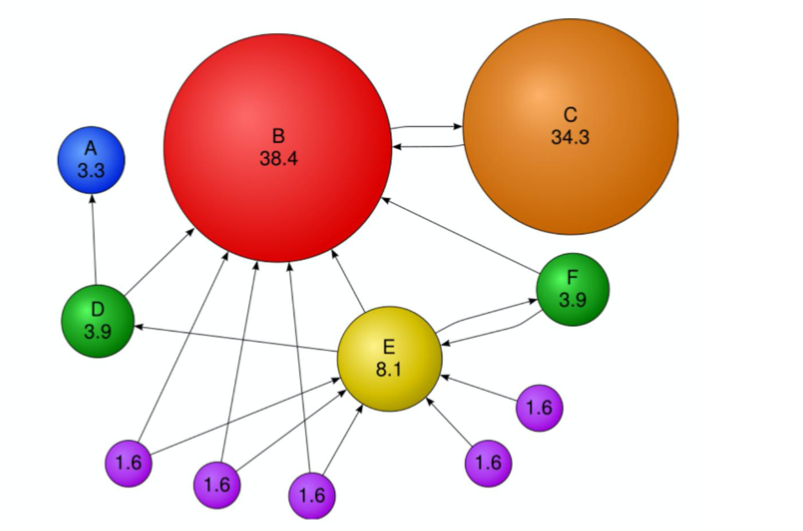
출처: Naver BoostCamp AI Tech - edwith 강의

✔️ 순간이동을 사용한 코드 구현
이때, 실제 코드구현에서는각 막다른 정점에서 간선을 모두 추가하면 간선을 많이 저장해야 함으로 이런 방법 보다는 각 계산마다 사라진 페이지 랭크값에 대하여 다시 저해주는 개념으로 구현을 하였다.(전체 vertex의 pagerank를 1로 유지하는 개념)

def pagerank(
    graph: Graph_dict,
    damping_factor: float,
    maxiters: int,
    tol: float,
) -> Dict[int, float]:
    vec: DefaultDict[int, float] = defaultdict(float)  # Pagerank vector

    """
    Initial setting to vertex
    """
    vertex_set = graph.nodes()
    vertex_set_len = len(vertex_set)  
    for v in vertex_set:
      vec[v] = (1/vertex_set_len)
    
    """
    iterate pagerank algorithm while pagerank values converged

    but we calcualte by computer
    so it may not converge specific value or need a lot of computing power.
    
    By setting Tolerance threshold, it is solved
    """
    itr = 0
    while itr < maxiters:
      # renewal pagerank logic
      # accumulate pagerank value to calculate vanising pagerank value
      # maintain total pagerank value to 1 
      S = 0
      vec_new : DefaultDict[int,float] = defaultdict(float)
      for v in vertex_set:
        for sv in vertex_set:
          out_neighbors = graph.out_neighbor(sv)
          if v in out_neighbors:
            vec_new[v] += (damping_factor * (vec[sv] / graph.out_degree(sv)))
        S += vec_new[v]

      # append vanished pagerank evenly
      append_rank = ((1 - S) / vertex_set_len)
      for v in vertex_set:
        vec_new[v] += append_rank

      # Stop the iteration if L1norm[PR(t) - PR(t-1)] < tol
      # check each pagerank value is lower than threshold
      delta: float = 0.0
      delta = l1_distance(vec_new, vec)

      
      vec = vec_new
      if delta < tol:
          break
      # replace vec
      vec = vec_new
      itr += 1

    return dict(vec)

Reference

Naver BoostCamp AI Tech - edwith 강의