크루스칼 알고리즘(Kruskal Algorithm)

*MST(Minimum Spanning Tree)

• Spanning Tree : 그래프 내의 모든 노드를 포함하는 트리

• Minimum Spanning Tree: Spanning Tree중에서 사용된 간선들의 가중치 합이 최소인 트리

*크루스칼 알고리즘(Kruskal Algorithm)

• 통신만, 도로망, 유통망의 길이, 구축비용, 전송시간 등을 최소로 구축하려는 경우

• Union Find 알고리즘이 적용됨(싸이클 판별)

• 무방향성, 가중치 그래프에서 사용됨

*문제상황

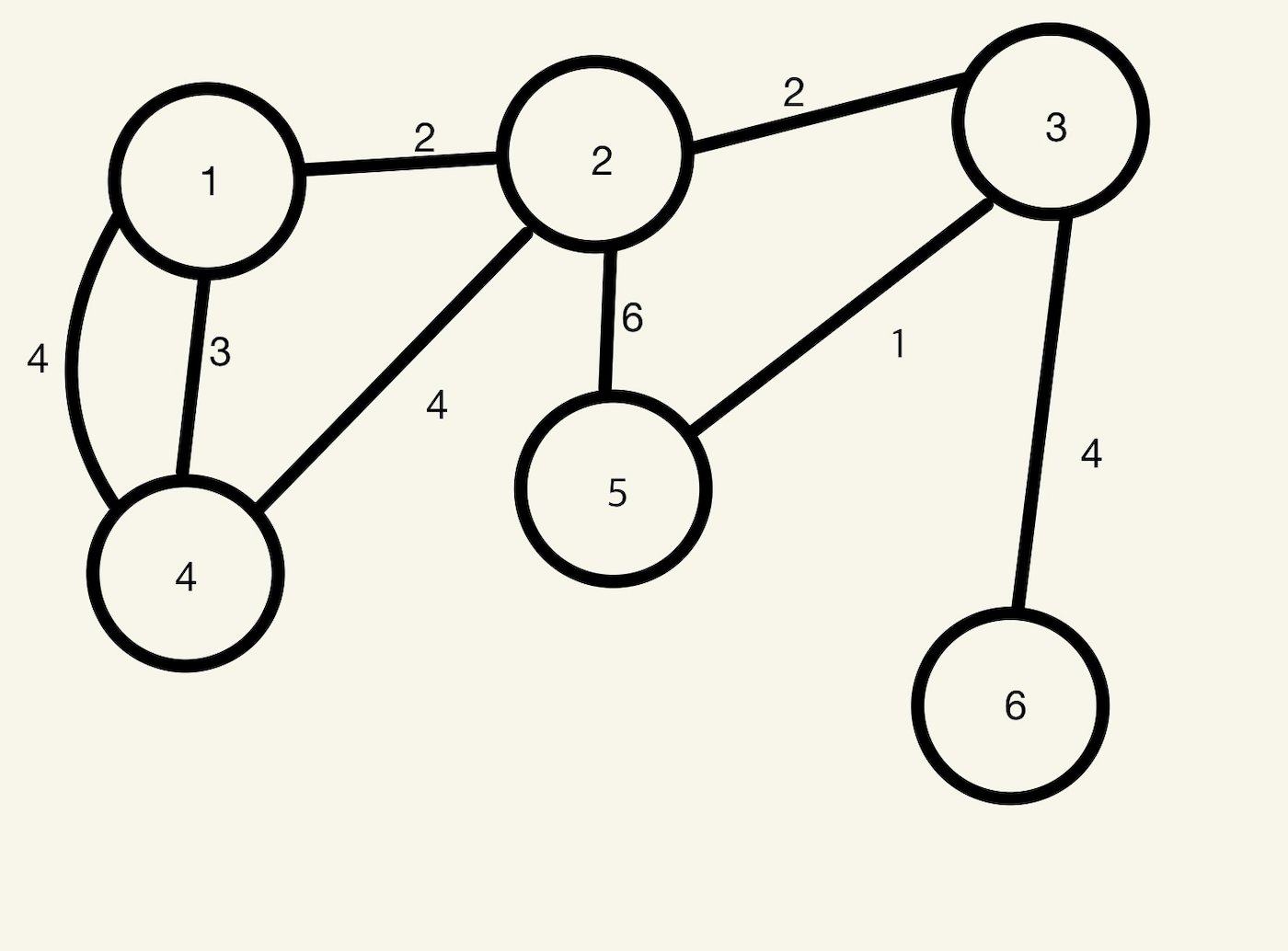
• 해당 그래프에서 모든 노드를 포한하는 트리가 되기 위해서 필요한 간선의 수보다 간선 수가 많다

• 간선의 가중치중 작은 간선을 검사를 하고 싸이클이 발생하지 않으면 해당 간선을 이어준다.

싸이클이란?

• 싸이클이 없는 경우
  
• 싸이클이 있는 경우
  

정리하자면 어느 한 노드를 출발하여 자기 자신으로 돌아올 수 있는 것을 싸이클이라고 한다.

MST를 만드는 과정에서(크루스칼 알고리즘 수행 시) 간선이 추가 될 시 싸이클이 생기게 된다면 이미 전단계의 어느 한 그룹은 부분적으로MST를 만들고 있다고 봐도 무방하다. 따라서 해당 간선을 추가하는 것은 불필요한 비용이 증가함으로 제외해야 한다.

• N개의 노드가 존재 할 때 모든 노드를 포함하는 트리를 만들기 위한 최소 간선의 수는 N-1개이다.

따라서, 간선을 N-1개를 이어주면 더이상 간선을 추가하지 않는다.

Step1 해당 노드와 가중치를 객체로써 관리하여 준다.

Step2 간선의 가중치를 기준으로 오름차순 정렬을 한다.

• 간선의 가중치를 최소로 하기 위해 간선의 가중치가 작은 것부터 검사를 하여 싸이클이 발생하지 않으면 노드를 이어주기 위함이다.
  

Step3 오른차순으로 정렬된 연결 정보를 탐색하면서 간선을 추가 하였을 때 싸이클이 발생하지 않는다면 간선을 연결한다.

Step4 간선을 N-1개 추가 할때까지 추가

import java.util.*;

public class KruskalAlgorithm{

    static int[] parent = new int[9];

    public static int findParent(int search){
        if(parent[search] == search) return search;

        return parent[search] = findParent(parent[search]);
    }

    public static void unionParent(int a, int b){
        int aParent = findParent(a);
        int bParent = findParent(b);

        parent[aParent] = bParent;
    }

    static class Edge implements Comparable<Edge>{
        int node1;
        int node2;
        int weight;

        public Edge(int node1, int node2, int weight){
            this.node1 = node1;
            this.node2 = node2;
            this.weight = weight;
        }

        @Override
        public int compareTo(Edge o) {
            return this.weight - o.weight;
        }
    }

    public static void main(String[] args){
        for(int i = 1 ; i < 9; i++){
            parent[i] = i;
        }

        int edgeCount = 0;
        List<Edge> result = new ArrayList<>();

        //step1
        List<Edge> arr = new ArrayList<>();
        arr.add(new Edge(1,2,2));
        arr.add(new Edge(1,4,4));
        arr.add(new Edge(1,4,3));
        arr.add(new Edge(2,4,4));
        arr.add(new Edge(2,3,2));
        arr.add(new Edge(2,5,6));
        arr.add(new Edge(5,3,1));
        arr.add(new Edge(3,6,4));

        //step2
        Collections.sort(arr);

        //stap3
        for(Edge e : arr){
            if(findParent(e.node1) != findParent(e.node2)){
                unionParent(e.node1,e.node2);
                result.add(new Edge(e.node1,e.node2,e.weight));
                edgeCount++;
            }
            if(edgeCount == 5) break;
        }

        //result
        for(Edge e : result){
            System.out.println("node1 : " + e.node1 + " node2 : " + e.node2 + " weight : " + e.weight);
        }

    }
}

이 글은 해당 블로그를 공부한 내용을 토대로 만들었습니다.
https://m.blog.naver.com/ndb796/221230967614