다익스트라 알고리즘(Dijstra Algorithm)

ganta·2021년 5월 29일

알고리즘

자료구조&알고리즘

목록 보기

3/4

다이나믹 프로그래밍을 활용한 최단경로 탐색 알고리즘
인공위성 GPS 소프트웨어 등에서 많이 사용이 됨
특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 찾아줌
무방향, 유방향 그래프 두 종류 다 작동을 함

*문제상황

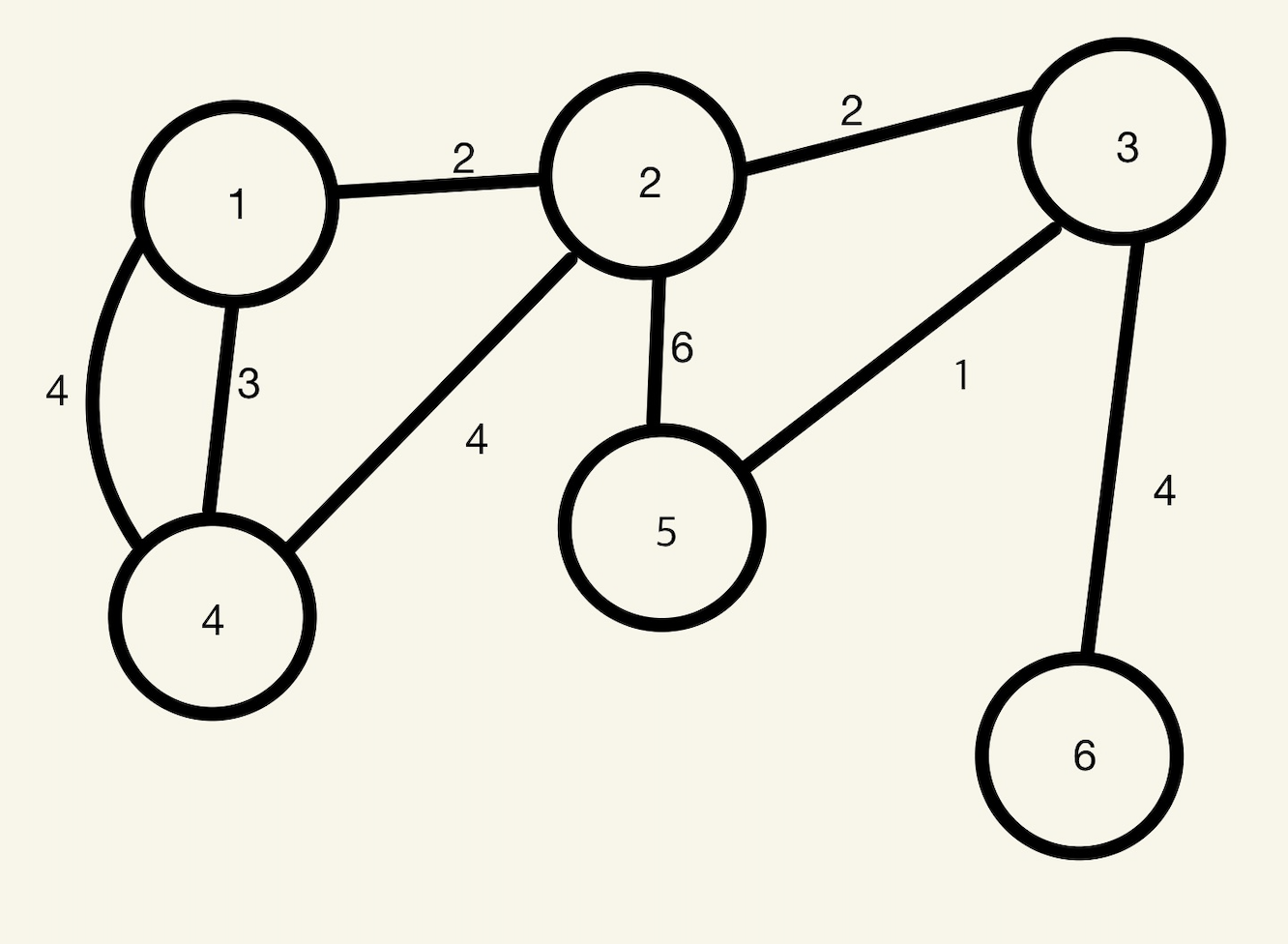
4번 노드에서 6번 노드로 가는 최단 경로를 찾아보자

출발 노드를 시작으로 노드를 하나씩 조사를 해 나아가는데 그 기준은 1) 조사를 아직 하지 않은 노드 중에서 2) 가장 최단거리로 갈 수 있는 노드를 조사하게 된다.
우선순위 큐를 이용하여 조사하는 노드들 중에서(조사하지 않은 노드 중) 현재 가장 최단거리로 갈 수 있는 노드를 조사

Step1 출발점에서 해당 노드까지 갈 수 있는 최단 경로의 가중치를 저장하는 일차원 배열을 생성한다. (result배열)

처음에는 무한대 값으로 모든 배열 부분에 저장(아주 큰 수)

Step2 출발 노드를 우선순위 큐에 저장 한 다음 각 노드에 대하여 갈 수 있는 최단 거리를 저장

Step3 조사를 하는 노드를 기준으로 이어져 있는 노드를 대상으로 현재 판단된 최단거리(result배열)보다 짧은 거리가 발견되면 우선순위 큐에 넣고 조사를 진행

Step4 우선순위 큐가 비어있을 때 까지 반복

이를 그림으로 나타내어 보면 다음과 같다.

4번 노드 조사
1번노드 조사
2번노드 조사
3번노드 조사
5번,6번노드는 위와 같은 방식으로 동일하게 조사
소스코드

import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;

public class DijstraAlgorithm {

    static final int INF = 10000000;

    static int[] result = new int[7];

    static class MapInfo{
        int node;
        int weight;

        public MapInfo(int node, int weight){
            this.node = node;
            this.weight = weight;
        }

    }

    static class Search implements Comparable<Search>{
        int adjacentNode;
        int weight;

        public Search(int adjacentNode,int weight){
            this.adjacentNode = adjacentNode;
            this.weight  =weight;
        }

        @Override
        public int compareTo(Search search) {
            return this.weight - search.weight;
        }
    }

    static void dijstra(int start, List<List<MapInfo>> map){
        result[start] = 0;
        PriorityQueue<Search> pq = new PriorityQueue<>();
        pq.add(new Search(4,0));

        while(!pq.isEmpty()){
            int searchNode = pq.peek().adjacentNode;
            int accumulateDist = pq.peek().weight;
            pq.poll();
            for(int i = 0 ; i < map.get(searchNode).size(); i++){
                int adjacentNode  = map.get(searchNode).get(i).node;
                int adjacentDist = accumulateDist + map.get(searchNode).get(i).weight;

                if(adjacentDist < result[adjacentNode]){
                    result[adjacentNode] = adjacentDist;
                    pq.add(new Search(adjacentNode,adjacentDist));
                }

            }

        }
    }

    public static void main(String[] args) {
        for(int i = 0 ; i < 7; i++){
            result[i] = INF;
        }

        //노드 연결정보 저장
        List<List<MapInfo>> map = new ArrayList<>();
        List<MapInfo> insert = new ArrayList<>();
        map.add(insert);
        insert = new ArrayList<>();

        insert.add(new MapInfo(2,2));
        insert.add(new MapInfo(4,3));
        insert.add(new MapInfo(4,4));
        map.add(insert);
        insert = new ArrayList<>();

        insert.add(new MapInfo(1,2));
        insert.add(new MapInfo(4,4));
        insert.add(new MapInfo(3,2));
        map.add(insert);
        insert = new ArrayList<>();

        insert.add(new MapInfo(2,2));
        insert.add(new MapInfo(5,1));
        insert.add(new MapInfo(6,4));
        map.add(insert);
        insert = new ArrayList<>();

        insert.add(new MapInfo(1,4));
        insert.add(new MapInfo(1,3));
        insert.add(new MapInfo(2,4));
        map.add(insert);
        insert = new ArrayList<>();

        insert.add(new MapInfo(2,6));
        insert.add(new MapInfo(3,1));
        map.add(insert);
        insert = new ArrayList<>();

        insert.add(new MapInfo(3,4));
        map.add(insert);

        dijstra(4,map);

        for(int i =1; i < 7 ; i++){
            System.out.println(i + ": " + result[i]);
        }
    }

}