전파 모형

ganta·2021년 2월 23일
Graph
0

Graph 이론

목록 보기
3/9
post-thumbnail

기술의 발달로 인하여 다양한 전파가 빠르게 이뤄지는 세상이 되어가고 있고이러한 전파 과정은 다양하고 매우 복잡하게 이뤄져 있다,
이를 체께적으로 이해하고 대처하기 위해서 다양한 수학적 모형화가 나왔고 그 중 기초적인 두 종류인 의사결정 기반의 전파 모형과 확률적 전파 모형을 정리 해 보았습니다.

의사결정 기반의 전파 모형

  • 의사결정 기반 전파 모형을 사용하는 경우 : 주변 사람들의 의사결정을 고려하여 각자 의사결정을 내리는 경우에 사용한다.

  • 의사결정 기반 전파 모형의 가장 간단한 형태 : 선형 임계치 모형(Linear Threshold Model)

  • 선형 임계치 모형(Linear Threshold Model)

    ✔️ 선형 임계치 모형이란?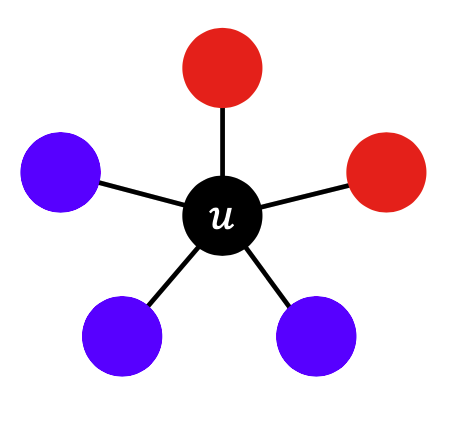
    출처: Naver BoostCamp AI Tech - edwith 강의

    👉 A를 선택한 정점을 붉은색, B를 선택한 비율을 푸른색이라고 가정
    👉 검은 정점이 붉은색을 선택 할 경우 행복이 2a 증가(붉은색 정점마다 행복도가 a씩 증가)
    👉 검은 정점이 푸른색을 선택 할 경우 행복이 3b 증가(푸른색 정점마다 행복도가 b씩 증가)
    👉 좀 더 일반화를 해 보게 되면 pp 비율의 이웃이 A를 선택하고 1−p1 - p 비율의 이웃이 B를 선택한다고 가정 하였을 시 검은 정점은 A를 ap>b(1−p)ap > b(1-p)일때 선택을 하게 된다. 이를 좀 더 정리하면 p>ba+bp > \frac{b}{a+b}일 때 이고 이를 임계치 qq라고 한다.
    ⭐️ 이러한 모형을 선형 임계치 모형이라고 한다.

    ✔️ 얼리 어답터
    👉 시드 집합(Seed Set)이라고도 한다.
    👉 위의 예시를 확장하여 전부 B를 사용하는 상황에서 A처음 사용하는 정점(얼리어답터)이 등장한다고 가정(이때, 임계치는 55%일 때)하였을 시 전파의 과정은 다음과 같다.

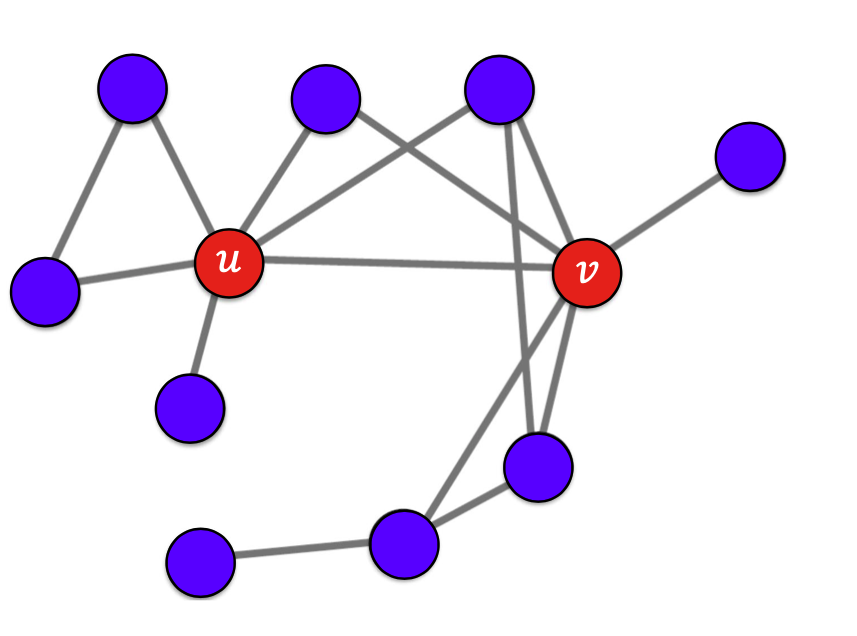
    출처: Naver BoostCamp AI Tech - edwith 강의


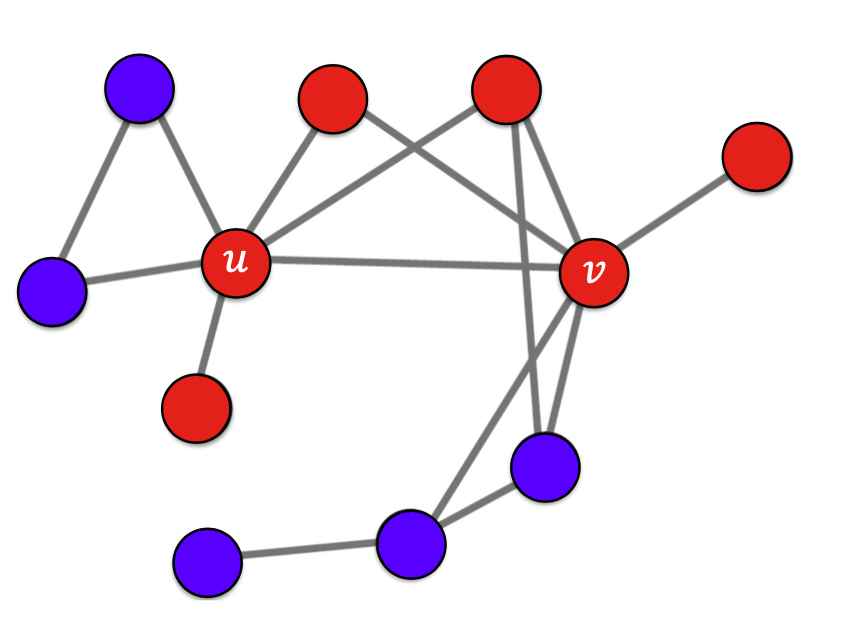
    출처: Naver BoostCamp AI Tech - edwith 강의


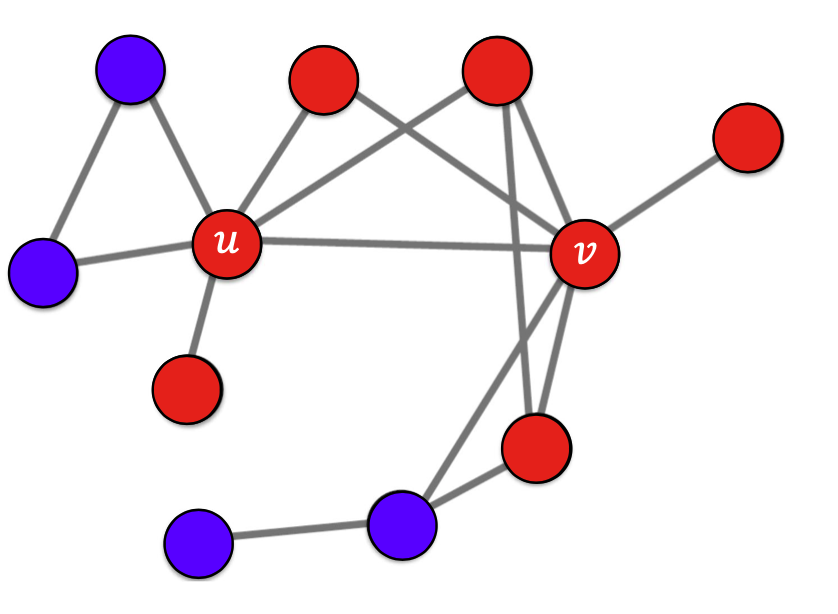
    출처: Naver BoostCamp AI Tech - edwith 강의


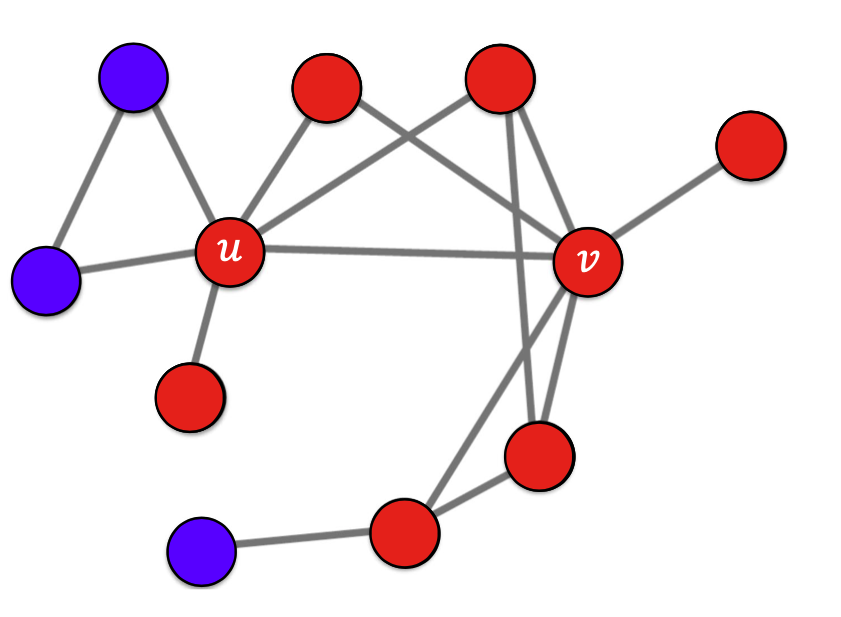
    출처: Naver BoostCamp AI Tech - edwith 강의


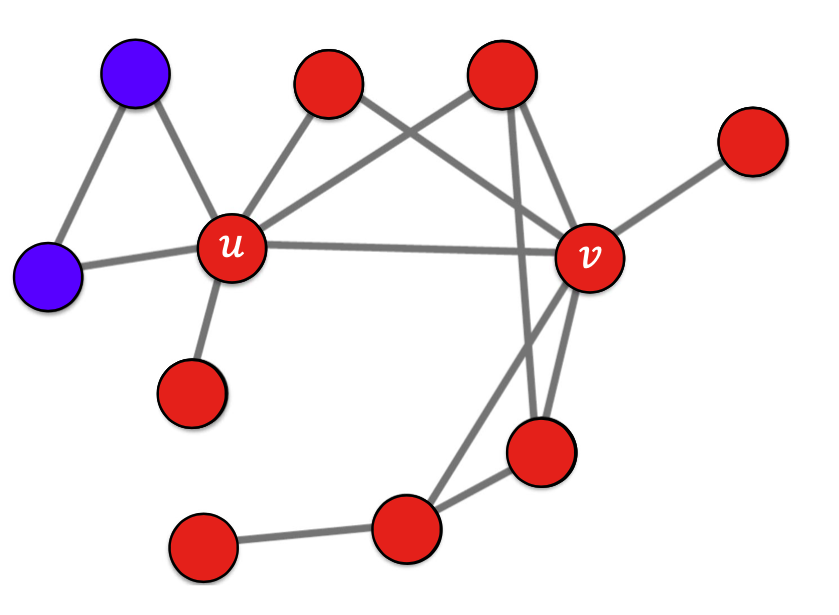
    출처: Naver BoostCamp AI Tech - edwith 강의

    ⭐️ 위를 통해 알 수 있는 점
    ➡️ 임게값은 전파가 어디까지 진행되는지 중요한 영향을 미친다.
    ➡️ 얼리 어답터가 어느 정점인지에 따라 전파에 큰 영향을 미친다.
    ➡️ 임계치를 넘는 경우가 없을 시 전파는 종료된다.

확률적 전파 모형

  • 확률적 전파 모형을 사용하는 경우 : 어느 정점의 의사에 따라 결정되는 것이 아닌 확률적으로 전파가 이뤄질 때 사용한다.(예를 들어 전염병의 전파같은 경우가 이에 해당한다.)

  • 확률적 전파 모형의 가장 간단한 형태 : 독립 전파 모형(Independent Cascade Model)

  • 독립 전파 모형(Independent Cascade Model)

    ✔️ 독립 전파 모형이란?

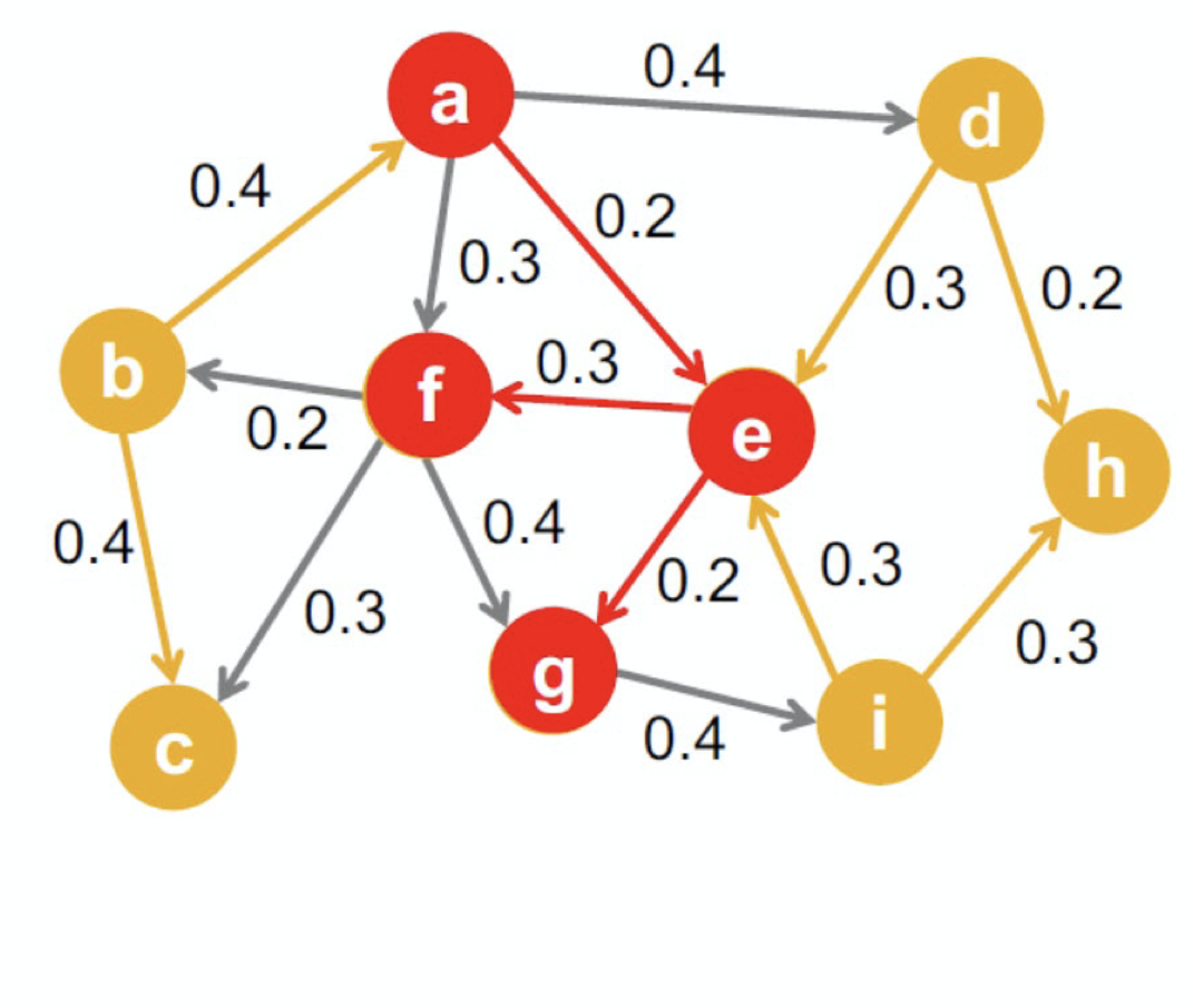
    출처: Naver BoostCamp AI Tech - edwith 강의

    👉 각 간선 (u,v)(u,v)의 가중치 puvp_{uv}는 uu가 감염되었을 때(vv가 감염되지는 않았을 때) uu가 vv를 감염시킬 확률에 해당한다.(이때, 서로 다른 이웃이 전염되는 확률은 독립적이다.)
    👉 모형의 모델은 최초 감염자들로부터 시작하고 첫 감염자들을 시드 집합(Seed Set)이라고 한다.
    👉 이 모형에서는 계속 감염자 산태로 남아있는 것을 가정하나 회복을 가정하는 SIS, SIR등의 다른 전파 모형이 존재한다.
    참고자료
    https://www.youtube.com/watch?v=S4v1xAlLeCI
    https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology

바이럴 마케팅과 전파 최대화 문제

  • 바이럴 마케팅이란 소비자들로 하여금 상품에 대한 긍정적인 입소문을 내게 하는 기법이다.

    ✔️ 소문의 시작점이 중요(의사결정 기반의 전파 모형에서 봤듯이 시작점에 따라 전파되는 범위가 영향을 받기 때문)


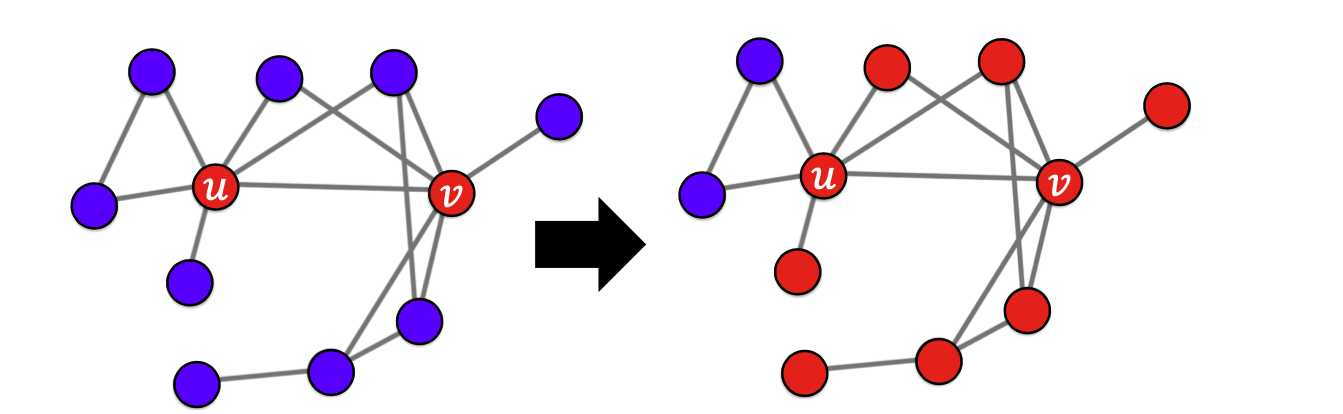
    출처: Naver BoostCamp AI Tech - edwith 강의


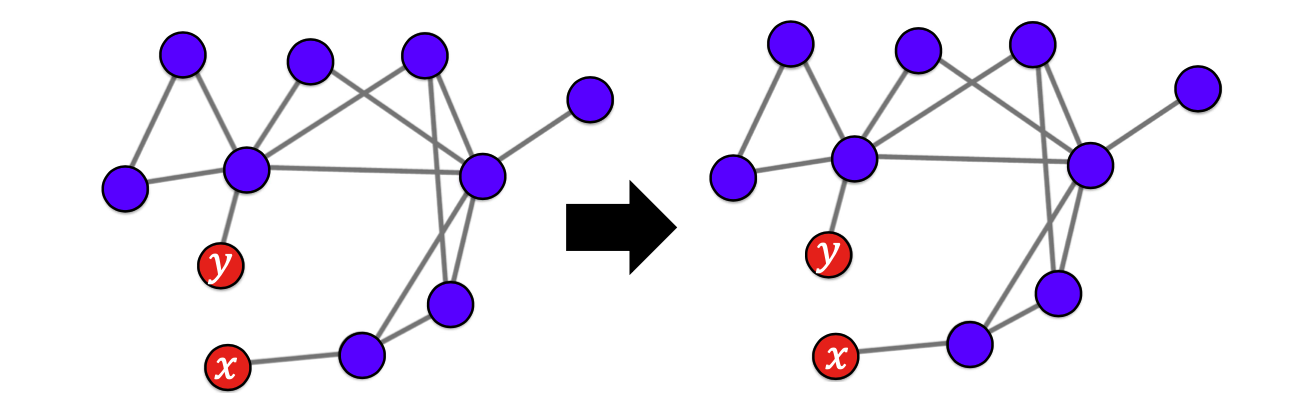
    출처: Naver BoostCamp AI Tech - edwith 강의

  • 시드 집합을 우리가 선택 할 수 있다면 그 결정은 매우 중요한 일이다.
    그래프, 전파 모형, 그리고 시드 집합의 크기가 주어졌을 때 전파를 최대화하는 시드 집합을 찾는 문제를 전파 최대화 문제(Influence Maximization)라고 한다.

  • 전파 최대화 문제(Influence Maximization)
    ✔️ 전파 최대화 문제는 굉장히 어려운 문제이다 .
    ✔️ 예를 들어 정점이 10,000개, 시드 집합이 10하였을 때 경우의 수는 2,743,355,077,591,282,538,321,819,720,749,000이라는 천문학적으로 높은 수치가 나타난다.
    ✔️ NP-hard문제임으로 증명이 되어져 있다.

    ❗️ 최고의 시드 집합을 찾기 대신 유망한 시드 집합을 찾는 방법으로는 정점 중심성 휴리스틱과 탐욕 알고리즘을 사용한다.

    ✔️ 정점 중심성 휴리스틱
    시드 집합의 크기가 kk개로 고정되어 있을 때, 정점의 중심성이 높은 순으로 kk개의 정점을 선택하는 방법이다.

    정점의 중심성으로는 페이지랭크 점수, 연결 중심성, 근접 중심성, 매개 중심성 등이 있다.
    ➡️ 합리적인 방법이지만, 최고의 시드 집합을 찾는다는 보장이 없다.

    ✔️ 탐욕 알고리즘
    시드 집합의 원소를 한번에 한 명씩 가장 전파력이 높은 전파자를 추가하는 방식이다.(이 과정을 목표하는 크기의 시드 집합에 도달할 때 까지 반복)

    탐욕 알고리즘 또한 전파 최대화 문제를 해결하는데 많이 쓰이는 알고리즘이다.

    이때, 확률적 전파 모형 중 하나인 독립 전파 모형에 경우, 이론적으로 정확도가 일부 보장이 된다. => 입력 그래프와 무관하게 다음 부등식이 성립

    탐욕 알고리즘으로 찾은 시드 집합의 의한 전파의 (평균)크기   ≥  (1−1e)∗\;\geq\;(1-\frac{1}{e}) * 최고의 시드 집합에 의한 전파의 (평균)크기 ≈\approx 0.632 ∗* 최고의 시드 집합에 의한 전파의 (평균)크기
    ⭐️ 즉, 탐욕 알고리즘의 최저 성능은 수학적으로 보장이 되어 있다.

Reference

Naver BoostCamp AI Tech - edwith 강의
https://www.youtube.com/watch?v=S4v1xAlLeCI
https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology

profile
ganta
한걸음씩 꾸준히
이전 포스트

페이지랭크

다음 포스트

군집 탐색

0개의 댓글