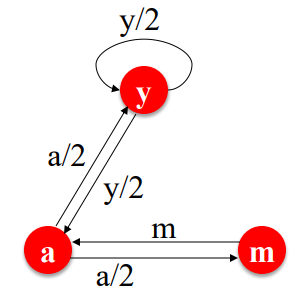
Link Analysis - PageRank(1)

Link Analysis

link analysis는 노드들의 연결과 관계를 분석하는데 사용되는 분석 기법이다.
웹 서칭시 어떤 페이지를 신뢰할 수 있는지(더 중요한지) 등을 판단하는데 도움을 줌.(모든 페이지들은 각기 다른 중요도를 가짐)
앞으로 말할 link는 Web 상의 링크(하이퍼링크)를 의미

Page Rank

• link를 vote로 생각 (당연히 vote 값은 페이지의 rank에 비례함)

• 링크 구조에서 페이지들의 순위를 정하는 기법으로 해당 노드로 들어오는(in-going) 링크가 많을 수록 순위가 높아짐.

• 모든 in-going link들을 동일하게 여기지는 않으며, 중요한 페이지/Rank가 높은 페이지에서 들어오는 링크들을 높게 쳐줌

• page rank를 계산하기 위해서는 반복적인 작업이 필요

  A -> B -> C 의 그래프가 있다고 가정하면 C의 rank를 계산하기 위해서는 B의 rank를 계산해야하고 마찬가지로 B의 rank를 계산하기 위해서는 A의 rank 값이 필요하다

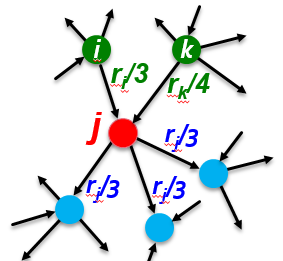
• 어떤 페이지 $j$, 그 페이지의 rank 값 $r_j$, 그리고 페이지의 out-going link가 $n$개 있다면 각 링크가 가지는 vote 값은 다음과 같다

  $vote = \frac{r_j}{n}$

  

• 위의 정보들을 종합하면 한 페이지의 rank값을 계산할 수 있다.

  $r_j=\sum_{i \rightarrow j}\frac{r_i}{d_i}\space (d: \#of\space outgoing\space link)$

• ex)

  

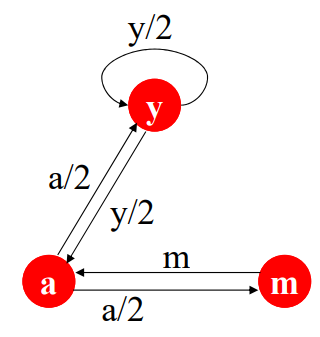
  위 그림에서 각 노드의 page rank는 다음과 같다.

  $r_y=0.5 \space r_a+0.5\space r_y \newline r_a=0.5 \space r_y+m\newline\newline r_m=0.5 \space r_a$

  ---

  $r_y=2/5,\space r_a=2/5, \space r_m=1/5\\ (r_y+r_a+r_m=1)$

• Stochastic adjacency matrix $M$

  • 연결 리스트를 행렬의 형태로 나타낸 것
  • $i\rightarrow j$가 존재한다면, $M_{ji}=1/d_i$ 없으면 $M_{ji}=0$
    • 여기서 M은 column stochastic matrix이다.(열의 합이 1임)
      
      
  • 이 행렬을 통해서 앞의 예제의 방정식들을 행렬의 연산 형태로 나타낼 수 있다.

    $\begin{bmatrix}r_y\\r_a\\r_m \end{bmatrix}=\begin{bmatrix}0.5&0.5&0\\0.5&0&1\\0&0.5&0 \end{bmatrix}\begin{bmatrix}r_y\\r_a\\r_m \end{bmatrix}$

    $r=M\cdot r$

    • 여기서 $r$은 $M$의 eigenvector이다.($Ax=\lambda x$를 만족하는 vector $x$, 위의 경우 eigenvalue = 1)

• Power Iteration Method

  • $r$ 값을 계산하기위한 방법

    initialize: $r^0 = [1/N,...,q/N]^T$
    iterate: $r^{t+1}= M\cdot r(t)$
    untill $|r^{t+1}-r^{t}|_1 < \epsilon$
    L2 norm등 다른 vetor norm을 사용해도 상관없음

• Random Walk Interpretation
  어떤 시간 $t$에서, 탐색자가 특정 페이지 $i$에 있다고 생각하면 $(t+1)$에 탐색자는 outgoing link를 타고 다른 노드로 이동할 것 그렇다면 t에서 각 페이지에 탐색자가 존재할 확률을 $p(t)$고 정의 해보면 다음과 같은 식이 성립한다.

  $p(t+1)=M\cdot p(t)$

  만일 여기서 $p(t+1)=p(t)$라면 수렴한 상태로 볼 수 있고, $p(t)$는 stationary distribution이다. 이는 우리가 위에서 사용한 $r=M\cdot r$ 과 동일한 형태이며 $r$ 또한 Random walk의 stationary distribution이다.
  Markrov processes에 따르면 특정조건(no-cycle, 모든 노드끼리의 길이 있음)을 만족하면 unique한 stationary distribution이 있음이 알려져있다.

  
  
  
  

Reference

https://en.wikipedia.org/wiki/Link_analysis
http://mmds.org/