PageRank의 세 가지 의문점
- 위의 식이 수렴하는가?
ex) 수렴하지 않는 경우(진동)
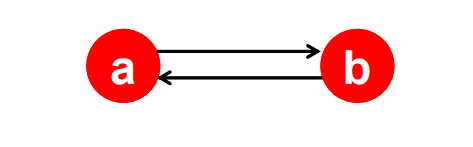
- 우리가 원하는 값으로 수렴하는가?
ex) 원하지 않는 값으로 수렴하는 경우
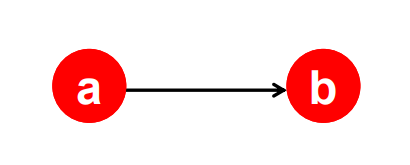
- 결과가 합리적인가
PageRank의 문제점
-
DeadEnd
- out-going link가 없음
- rank의 누수가 발생함
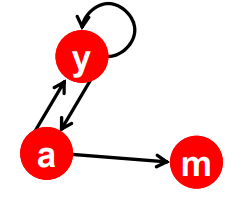
- 초기의 rank값은 각각 1/3이지만 수렴한 뒤에 값을 보면 이되며, 초기에 rank 값의 합이 1이었지만 0으로 변한 것을 볼 수 있다. rank값의 누수(leak out)가 발생한 것
- 애초에 m 때문에 stochastic하지 않다.
-
Spider traps
- 내부의 사이클에 갇힘
- 모든 rank값을 흡수함
- 즉 수렴하긴 하지만, 우리가 원하는 값이 아님
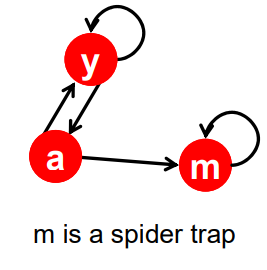
노드 m에 들어오면 사이클에 갇히게된다. 초기의 rank값은 각각 1/3이지만 수렴한 뒤에 값을 보면 이되며, m이 다른 노드들의 랭크값을 흡수한다.
-
Solution: Teleport
- 위의 상황들에 직면하면 확률에 의해 임의의 점으로 이동시킨다.
- 의 확률로 기존 과정을 진행하고, 확률로 다른 점으로 이동한다.
- 의 값은 0.8, 0.9를 사용한다고 알려져 있다.
- Dead end의 경우 행렬을 column stochastic하게 만들어 줘야함
이 경우 행렬의 m열을 수정해야한다.(0 to 1/3)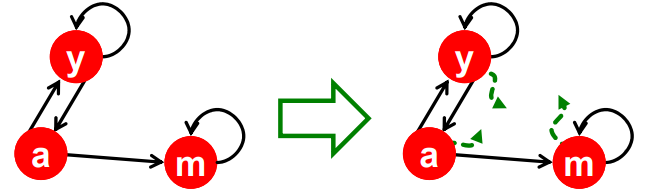

Google's solution
-
PageRank equation
-
Google Matrix A
-
Google's PageRank equation
- 이 방정식을 통해 계산을 할 때 많은 시간과 자원이 필요 (A is Dense matrix)
PageRank의 효율적인 계산법
-
를 계산하는데(특히 행렬의 곱) 충분한 메모리 자원이 있다면 좋겠지만 그렇지 않다
- 10억개의 페이지가 있다면 행렬 A는 개의 요소를 가진다. 각 요소가 차지하는 메모리 까지 계산하면 결코 작은수가 아니다.
-
를 정리해보자
- 먼저 teleport 각 페이지의 rank에서 만큼의 세금을 뗀 것이라 생각하고 이를 마지막에 분배
다소 복잡해 보이지만, 확실히 정돈되었다고 할 수 있다. 왜? M은 희소행렬이기에 메모리도 적게 먹고, 빠르다.
또한 Dead end가 발생 한 경우 보다 큰 값인 를 더해준다. (S는 누수의 합)
- 먼저 teleport 각 페이지의 rank에서 만큼의 세금을 뗀 것이라 생각하고 이를 마지막에 분배
-
위에서 정리한 식을 바탕으로 Page Rank를 계산하는 Cost
- 메인 메모리가 를 담기에 충분하다면
- 디스크에서 과 을 읽어들인다.
- 디스크에 를 기록한다
- Cost per iteration =
- 메인 메모리가 부족하다면?
(1) 를 k개의 block으로 나눠서 업데이트- 매번 M과 를 디스크에서 읽어야함
- Cost =
- 각 stripe는 에서 해당하는 목적지 정보만을 가지고 있음
- 을 번 호출하는 사태는 생기지 않지만 약간의 중복이 발생함
- Cost =
- 메인 메모리가 를 담기에 충분하다면
Reference
