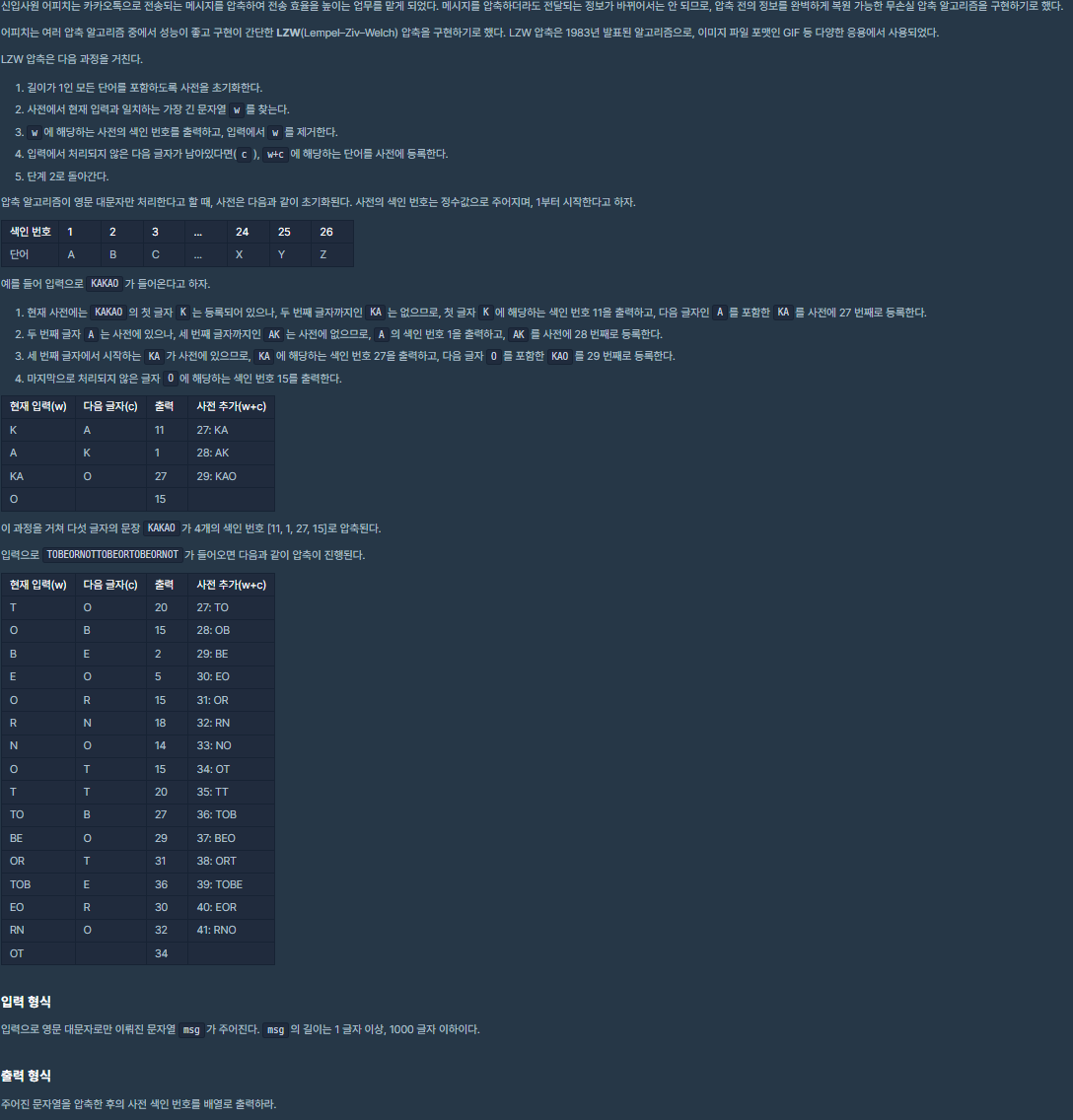
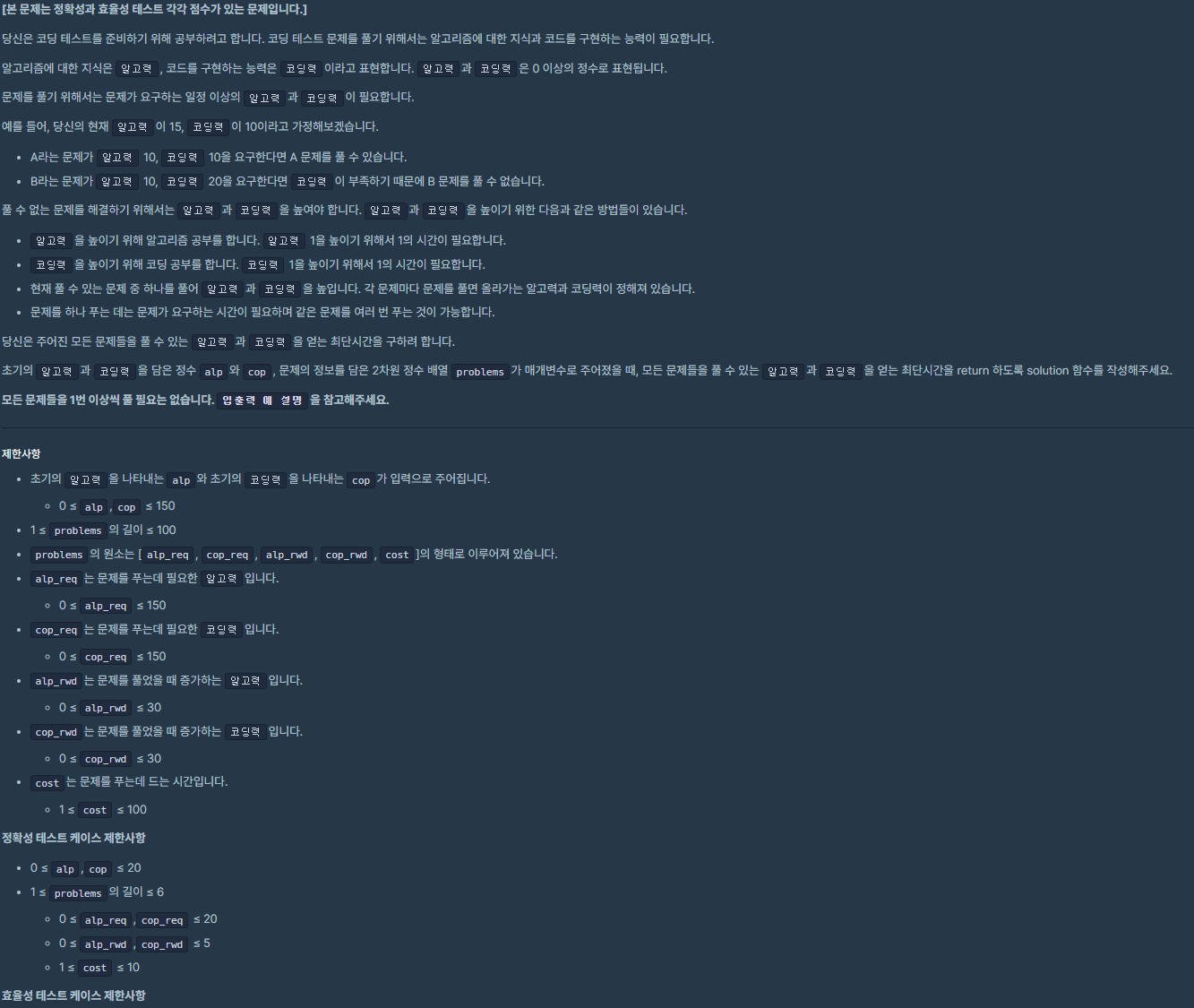
1. [3차] 압축
1) 문제
2) 문제 분석 및 풀이
1) 설계, 분석
이므로 까지 가능.
- 한 글자씩 해쉬테이블에 삽입해 초기화
- 맨 앞글자부터 하나씩 늘려가며 맵에 있는지 확인 (k 확인 ka 확인 kak.. 이런식으로)
- 있으면 넘어감
- 없으면 해쉬테이블에 삽입
- ka가 테이블에 없다면 k의 값을 출력하고 ka를 새로 삽입.
2) 풀이
#include <string>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <iostream>
using namespace std;
vector<int> solution(string msg)
{
vector<int> answer;
unordered_map<string, int> pressMap;
int cnt=0;
for (auto& c : msg)
{
string s(1,c);
pressMap[s] = c- 'A' + 1;
}
string currStr="";
for (int i=0; i<msg.size(); i++)
{
currStr += msg[i];
// 못찾으면 추가
if (i == msg.size()-1 || pressMap.find(currStr + msg[i+1]) == pressMap.end())
{
answer.push_back(pressMap[currStr]);
if (i != msg.size()-1)
pressMap[currStr + msg[i+1]] = 27 + (cnt++);
currStr="";
}
}
return answer;
}2. 코딩 테스트 공부
1) 문제
2) 문제 분석 및 풀이
1) 설계, 분석
alp, cop <= 150 이니까 까지 가능할 듯
- 초기 상태에서 목표까지 가는 최소비용을 구하는 문제 -> 다익스트라 사용
- 다익스트라를 2차원 배열에 적용 dijk[alp][cop] : alp,cop까지 오는데 최소 비용
2) 풀이
#include <string>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
int solution(int alp, int cop, vector<vector<int>> problems)
{
int answer = 0;
int alpMax = alp;
int copMax = cop;
for (auto& problem : problems)
{
alpMax = max(alpMax, problem[0]);
copMax = max(copMax, problem[1]);
}
//거리 배열
vector<vector<int>> dijkDistVec(alpMax+1, vector<int>(copMax+1, 1000));
//방문 배열
vector<vector<bool>> visited(alpMax+1, vector<bool>(copMax+1, false));
// 알고리즘 공부, 코딩 공부 삽압.
problems.push_back({0,0,1,0,1});
problems.push_back({0,0,0,1,1});
// 시간이 낮은게 위로오게
// 코스트가 낮은게 먼저
priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;
dijkDistVec[alp][cop] = 0;
// 시간 알고 코딩
// 지금 알고력 코딩력까지 도달하는데 걸린 최소 비용
pq.push({dijkDistVec[alp][cop], alp, cop});
while(!pq.empty())
{
auto top = pq.top();
pq.pop();
int topAlp = top[1];
int topCop = top[2];
int currCost = top[0];
//같은 알고/코딩력인데 누가 방문했다 -> 더 적은 코스트가 있었다.
//넘어감.
if (visited[topAlp][topCop]) continue;
visited[topAlp][topCop] = true;
for (auto& problem : problems)
{
// 문제의 요구치 미달 -> 건너뜀
if (topAlp < problem[0] || topCop < problem[1]) continue;
// 문제를 풀고 난 후 알고/코딩력
int nAlp = min(alpMax, topAlp + problem[2]);
int nCop = min(copMax, topCop + problem[3]);
// 기존 값과 문제를 푼뒤의 값중 작은걸로 갱신하고 queue에 넣기
dijkDistVec[nAlp][nCop] = min(dijkDistVec[topAlp][topCop] + problem[4], dijkDistVec[nAlp][nCop]);
pq.push({dijkDistVec[nAlp][nCop], nAlp, nCop});
}
}
return dijkDistVec[alpMax][copMax];
}3. 두 큐 합 같게 만들기
1) 문제
문제 설명
길이가 같은 두 개의 큐가 주어집니다. 하나의 큐를 골라 원소를 추출(pop)하고, 추출된 원소를 다른 큐에 집어넣는(insert) 작업을 통해 각 큐의 원소 합이 같도록 만들려고 합니다. 이때 필요한 작업의 최소 횟수를 구하고자 합니다. 한 번의 pop과 한 번의 insert를 합쳐서 작업을 1회 수행한 것으로 간주합니다.큐는 먼저 집어넣은 원소가 먼저 나오는 구조입니다. 이 문제에서는 큐를 배열로 표현하며, 원소가 배열 앞쪽에 있을수록 먼저 집어넣은 원소임을 의미합니다. 즉, pop을 하면 배열의 첫 번째 원소가 추출되며, insert를 하면 배열의 끝에 원소가 추가됩니다. 예를 들어 큐 [1, 2, 3, 4]가 주어졌을 때, pop을 하면 맨 앞에 있는 원소 1이 추출되어 [2, 3, 4]가 되며, 이어서 5를 insert하면 [2, 3, 4, 5]가 됩니다.
다음은 두 큐를 나타내는 예시입니다.
queue1 = [3, 2, 7, 2]
queue2 = [4, 6, 5, 1]
두 큐에 담긴 모든 원소의 합은 30입니다. 따라서, 각 큐의 합을 15로 만들어야 합니다. 예를 들어, 다음과 같이 2가지 방법이 있습니다.queue2의 4, 6, 5를 순서대로 추출하여 queue1에 추가한 뒤, queue1의 3, 2, 7, 2를 순서대로 추출하여 queue2에 추가합니다. 그 결과 queue1은 [4, 6, 5], queue2는 [1, 3, 2, 7, 2]가 되며, 각 큐의 원소 합은 15로 같습니다. 이 방법은 작업을 7번 수행합니다.
queue1에서 3을 추출하여 queue2에 추가합니다. 그리고 queue2에서 4를 추출하여 queue1에 추가합니다. 그 결과 queue1은 [2, 7, 2, 4], queue2는 [6, 5, 1, 3]가 되며, 각 큐의 원소 합은 15로 같습니다. 이 방법은 작업을 2번만 수행하며, 이보다 적은 횟수로 목표를 달성할 수 없습니다.
따라서 각 큐의 원소 합을 같게 만들기 위해 필요한 작업의 최소 횟수는 2입니다.길이가 같은 두 개의 큐를 나타내는 정수 배열 queue1, queue2가 매개변수로 주어집니다. 각 큐의 원소 합을 같게 만들기 위해 필요한 작업의 최소 횟수를 return 하도록 solution 함수를 완성해주세요. 단, 어떤 방법으로도 각 큐의 원소 합을 같게 만들 수 없는 경우, -1을 return 해주세요.
제한사항
1 ≤ queue1의 길이 = queue2의 길이 ≤ 300,000
1 ≤ queue1의 원소, queue2의 원소 ≤ 109
주의: 언어에 따라 합 계산 과정 중 산술 오버플로우 발생 가능성이 있으므로 long type 고려가 필요합니다.
입출력 예
queue1 queue2 result
[3, 2, 7, 2][4, 6, 5, 1] 2
[1, 2, 1, 2][1, 10, 1, 2] 7
[1, 1][1, 5] -1
2) 문제 분석 및 풀이
1) 설계, 분석
이므로 까지 가능.
- 각 큐 원소들의 합을 구한다.
- 이 과정에서 각 큐의 최대를 구한다.
- target = 두 큐의 합 / 2를 구한다.
- 각 큐의 최댓값중 target보다 큰 값이 있으면 조건을 만족하는 경우가 없다.
- 다음을 반복한다.
- 각 큐의 합이 동일하면 종료
- 각 큐의 합을 비교
- 큰 쪽에서 pop 작은 쪽에 push
- count가 일정 횟수를 넘으면 안된다고 판단
2) 풀이
#include <string>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
int solution(vector<int> queue1, vector<int> queue2)
{
int answer = 0;
long long sum1 = 0;
long long sum2 = 0;
long long total = 0LL;
int max1 = 0;
int max2 = 0;
queue<int> q1;
queue<int> q2;
for (auto& f1 : queue1)
{
q1.push(f1);
max1 = max(max1, f1);
sum1 += f1;
}
for (auto& f2 : queue2)
{
q2.push(f2);
max2 = max(max2, f2);
sum2 += f2;
}
total = sum1 + sum2;
if (total % 2 != 0) return -1;
if (total / 2 < max1) return -1;
if (total / 2 < max2) return -1;
while(true)
{
if (answer > 600'000) return -1;
if (sum1 == sum2) break;
if (sum1 > sum2)
{
sum1 -= q1.front();
sum2 += q1.front();
q2.push(q1.front());
q1.pop();
}
else
{
sum1 += q2.front();
sum2 -= q2.front();
q1.push(q2.front());
q2.pop();
}
answer++;
}
return answer;
}4. 숫자 게임
1) 문제
문제 설명
xx 회사의 2xN명의 사원들은 N명씩 두 팀으로 나눠 숫자 게임을 하려고 합니다. 두 개의 팀을 각각 A팀과 B팀이라고 하겠습니다. 숫자 게임의 규칙은 다음과 같습니다.먼저 모든 사원이 무작위로 자연수를 하나씩 부여받습니다.
각 사원은 딱 한 번씩 경기를 합니다.
각 경기당 A팀에서 한 사원이, B팀에서 한 사원이 나와 서로의 수를 공개합니다. 그때 숫자가 큰 쪽이 승리하게 되고, 승리한 사원이 속한 팀은 승점을 1점 얻게 됩니다.
만약 숫자가 같다면 누구도 승점을 얻지 않습니다.
전체 사원들은 우선 무작위로 자연수를 하나씩 부여받았습니다. 그다음 A팀은 빠르게 출전순서를 정했고 자신들의 출전 순서를 B팀에게 공개해버렸습니다. B팀은 그것을 보고 자신들의 최종 승점을 가장 높이는 방법으로 팀원들의 출전 순서를 정했습니다. 이때의 B팀이 얻는 승점을 구해주세요.
A 팀원들이 부여받은 수가 출전 순서대로 나열되어있는 배열 A와 i번째 원소가 B팀의 i번 팀원이 부여받은 수를 의미하는 배열 B가 주어질 때, B 팀원들이 얻을 수 있는 최대 승점을 return 하도록 solution 함수를 완성해주세요.제한사항
A와 B의 길이는 같습니다.
A와 B의 길이는 1 이상 100,000 이하입니다.
A와 B의 각 원소는 1 이상 1,000,000,000 이하의 자연수입니다.
입출력 예
A B result
[5,1,3,7][2,2,6,8] 3
[2,2,2,2][1,1,1,1] 0
2) 문제 분석 및 풀이
1) 설계, 분석
이므로 까지 가능.
- A,B를 정렬
- A를 순회 (i)
- B가 비어있으면 종료
- B에서 A(i) 보다 같거나 큰 원소중에 최소를 뽑아서 배치
- B에서 해당 값 삭제
2) 풀이
#include <string>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
int answer = 0;
// B직원이 이기도록 배치하는데 최소한의 숫자를 넣자
// 가장 최소의 숫자로 이기도록
// A가 2면 3 , 4 , 5 중에 3을 먼저 넣자
int solution(vector<int> A, vector<int> B)
{
map<int,int> BEcnt;
sort(A.begin(), A.end());
//map에 B값의 개수를 업데이트
for (auto& b : B)
{
BEcnt[b]++;
}
int maxA = *max_element(A.begin(), A.end());
int maxB = *max_element(B.begin(), B.end());
int minA = *min_element(A.begin(), A.end());
int minB = *min_element(B.begin(), B.end());
// B의 모든 원소가 A보다 크면 전원 승리
if (maxA < minB) return A.size();
// B의 모든 원소가 A보다 작거나 같으면 패배 및 무승부
if (minA >= maxB) return 0;
for (int i=0; i<A.size(); i++)
{
if (BEcnt.size() == 0) break;
// map에서 A[i]보다 큰 원소가 처음 나오는 위치
auto it = BEcnt.upper_bound(A[i]);
// 값이 있다면
if (it != BEcnt.end())
{
// 점수+1
answer++;
int key = it->first;
// 해당 수의 개수 감소 및 삭제
BEcnt[key]--;
if (BEcnt[key] == 0)
BEcnt.erase(key);
}
}
return answer;
}6. k진수에서 소수 개수 구하기
1) 문제
양의 정수 n이 주어집니다. 이 숫자를 k진수로 바꿨을 때, 변환된 수 안에 아래 조건에 맞는 소수(Prime number)가 몇 개인지 알아보려 합니다.
0P0처럼 소수 양쪽에 0이 있는 경우
P0처럼 소수 오른쪽에만 0이 있고 왼쪽에는 아무것도 없는 경우
0P처럼 소수 왼쪽에만 0이 있고 오른쪽에는 아무것도 없는 경우
P처럼 소수 양쪽에 아무것도 없는 경우
단, P는 각 자릿수에 0을 포함하지 않는 소수입니다.
예를 들어, 101은 P가 될 수 없습니다.
예를 들어, 437674을 3진수로 바꾸면 211020101011입니다. 여기서 찾을 수 있는 조건에 맞는 소수는 왼쪽부터 순서대로 211, 2, 11이 있으며, 총 3개입니다. (211, 2, 11을 k진법으로 보았을 때가 아닌, 10진법으로 보았을 때 소수여야 한다는 점에 주의합니다.) 211은 P0 형태에서 찾을 수 있으며, 2는 0P0에서, 11은 0P에서 찾을 수 있습니다.정수 n과 k가 매개변수로 주어집니다. n을 k진수로 바꿨을 때, 변환된 수 안에서 찾을 수 있는 위 조건에 맞는 소수의 개수를 return 하도록 solution 함수를 완성해 주세요.
2) 문제 분석 및 풀이
1) 설계, 분석
이므로 까지 가능
k진수로 변환하니까 문자열의 길이가 3배정도 길어질 수도
1,000,000의 길이가 3배 늘어남 -> 숫자에 10억을 넘어가지 int로는 오버플로우 발생가능
- 해당 숫자를 k진수로 변환
- 문자의 왼쪽부터 시작해서 오른쪽으로 진행
- 다음 문자가 0
- 소수 판별
- 다음 문자가 0이 아니면
- 값 갱신
- 다음 문자가 0
,는 n을 k 진수로 변환한 수를 10진수로 읽었을때 최대 값.
ex) 1,000,000을 3진수로 변환 -> 1202111122221_3
이걸 10진수로 보면 1,202,111,122,221
2) 풀이
#include <string>
#include <vector>
#include <cmath>
using namespace std;
bool PrimeCheck(long long num)
{
if (num == 1) return false;
for (int i=2; i<=sqrt(num); i++)
{
if (num % i == 0) return false;
}
return true;
}
vector<int> DeciToK(int n, int k)
{
vector<int> remain;
while (n)
{
remain.push_back(n % k);
n /= k;
}
return vector<int>(remain.rbegin(), remain.rend());
}
int solution(int n, int k)
{
int answer = 0;
// k진수 변환
vector<int> afterTrans = DeciToK(n,k);
afterTrans.push_back(0);
long long num = 0;
for (int i=0; i<afterTrans.size(); i++)
{
//0. i번째 숫자가 0이면
if (afterTrans[i] == 0)
{
//0-1 현재 num이 0인 경우는 넘어감
if (num == 0) continue;
//0-2 num이 0이 아니면 num 소수 판별 후 num 초기화
if (PrimeCheck(num)) answer++;
num = 0;
}
//0. i번째 숫자가 0이 아니면, num update
else
{
num = num * 10 + afterTrans[i];
}
}
return answer;
}7. 거리두기 확인하기
1) 문제
개발자를 희망하는 죠르디가 카카오에 면접을 보러 왔습니다.
코로나 바이러스 감염 예방을 위해 응시자들은 거리를 둬서 대기를 해야하는데 개발 직군 면접인 만큼
아래와 같은 규칙으로 대기실에 거리를 두고 앉도록 안내하고 있습니다.대기실은 5개이며, 각 대기실은 5x5 크기입니다.
거리두기를 위하여 응시자들 끼리는 맨해튼 거리1가 2 이하로 앉지 말아 주세요.
단 응시자가 앉아있는 자리 사이가 파티션으로 막혀 있을 경우에는 허용합니다.
5개의 대기실을 본 죠르디는 각 대기실에서 응시자들이 거리두기를 잘 기키고 있는지 알고 싶어졌습니다. 자리에 앉아있는 응시자들의 정보와 대기실 구조를 대기실별로 담은 2차원 문자열 배열 places가 매개변수로 주어집니다. 각 대기실별로 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
2) 문제 분석 및 풀이
1) 설계, 분석
이므로 까지 가능. 상당히 많은 연산을 필요로 할지도..
- 격자 배열을 순회
- 현재 위치가 P
- 오른쪽 2칸 확인
- 1칸 거리에 칸막이가 있으거나 사람이 없으면 만족
- 2칸 거리에 사람이 없으면 만족
- 아래쪽 2칸 확인
- 1칸 거리에 칸막이가 있으거나 사람이 없으면 만족
- 2칸 거리에 사람이 없으면 만족
- 우하단 대각 확인
- 현재칸 기준 오른쪽, 아래쪽 칸막이 있으면 만족
- 우하단 칸에 사람이 있으면 만족
- 우상단 대각 확인
- 현재칸 기준 오른쪽 위쪽 칸막이 있으면 만족
- 우상단 칸에 사람이 있으면 만족
- 오른쪽 2칸 확인
- 현재 위치가 P
2) 풀이
#include <string>
#include <vector>
#include <iostream>
using namespace std;
vector<int> answer;
// r, rr, d, dd, dr, ru
int dx[6] = {0,0,1,2,1,-1};
int dy[6] = {1,2,0,0,1,1};
bool PosCheck(int nx, int ny)
{
if (0 > nx || nx >= 5) return false;
if (0 > ny || ny >= 5) return false;
return true;
}
void simulate(vector<string> place)
{
for (int i=0; i<5; i++)
{
for (int j=0; j<5; j++)
{
if (place[i][j] == 'P')
{
bool flag = true;
int nx;
int ny;
// 오른쪽
for (int k=0; k<2; k++)
{
nx = i+dx[k];
ny = j+dy[k];
if(!PosCheck(nx, ny)) break;
if (place[nx][ny] == 'X') break;
if (place[nx][ny] == 'P') flag = false;
}
// 아래쪽
for (int k=2; k<4; k++)
{
nx = i+dx[k];
ny = j+dy[k];
if(!PosCheck(nx, ny)) break;
if (place[nx][ny] == 'X') break;
if (place[nx][ny] == 'P') flag = false;
}
// 우하단
nx = i+dx[4];
ny = j+dy[4];
if(PosCheck(nx, ny))
{
if (place[nx][ny] == 'P' && !(place[nx-1][ny] == 'X' && place[nx][ny-1] == 'X')) flag = false;
}
// 우상단
nx = i+dx[5];
ny = j+dy[5];
if(PosCheck(nx, ny))
{
if (place[nx][ny] == 'P' && !(place[nx+1][ny] == 'X' && place[nx][ny-1] == 'X')) flag = false;
}
if (flag == false) { answer.push_back(0); return;}
}
}
}
answer.push_back(1);
}
vector<int> solution(vector<vector<string>> places)
{
for (auto& place : places)
simulate(place);
return answer;
}