알고리즘 스터디 55일차

1. [3차] 압축

1) 문제

문제 설명
명이 입국심사를 위해 줄을 서서 기다리고 있습니다. 각 입국심사대에 있는 심사관마다 심사하는데 걸리는 시간은 다릅니다.

처음에 모든 심사대는 비어있습니다. 한 심사대에서는 동시에 한 명만 심사를 할 수 있습니다. 가장 앞에 서 있는 사람은 비어 있는 심사대로 가서 심사를 받을 수 있습니다. 하지만 더 빨리 끝나는 심사대가 있으면 기다렸다가 그곳으로 가서 심사를 받을 수도 있습니다.

모든 사람이 심사를 받는데 걸리는 시간을 최소로 하고 싶습니다.

입국심사를 기다리는 사람 수 n, 각 심사관이 한 명을 심사하는데 걸리는 시간이 담긴 배열 times가 매개변수로 주어질 때, 모든 사람이 심사를 받는데 걸리는 시간의 최솟값을 return 하도록 solution 함수를 작성해주세요.

제한사항
입국심사를 기다리는 사람은 1명 이상 1,000,000,000명 이하입니다.
각 심사관이 한 명을 심사하는데 걸리는 시간은 1분 이상 1,000,000,000분 이하입니다.
심사관은 1명 이상 100,000명 이하입니다.

입출력 예
n times return
6 [7, 10] 28

2) 문제 분석 및 풀이

1) 설계, 분석

2) 풀이

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

long long solution(int n, vector<int> times) 
{
    long long answer = 0;
    sort(times.begin(), times.end());

    long long left = 1;
    long long right = (long long)times.back() * n;

    while (left <= right) 
    {
        long long mid = (left + right) / 2;
        long long people = 0;

        for (int t : times) 
        {
            people += mid / t;
            if (people >= n) break;
        }

        if (people >= n) 
        {
            answer = mid;
            right = mid - 1;
        }
        else 
            left = mid + 1;
    }
    return answer;
}

2. 트리 트리오 중간값

1) 문제

문제 설명
n개의 점으로 이루어진 트리가 있습니다. 이때, 트리 상에서 다음과 같은 것들을 정의합니다.

어떤 두 점 사이의 거리는, 두 점을 잇는 경로 상 간선의 개수로 정의합니다.
임의의 3개의 점 a, b, c에 대한 함수 f(a, b, c)의 값을 a와 b 사이의 거리, b와 c 사이의 거리, c와 a 사이의 거리, 3개 값의 중간값으로 정의합니다.
트리의 정점의 개수 n과 트리의 간선을 나타내는 2차원 정수 배열 edges가 매개변수로 주어집니다. 주어진 트리에서 임의의 3개의 점을 뽑아 만들 수 있는 모든 f값 중에서, 제일 큰 값을 구해 return 하도록 solution 함수를 완성해주세요.

제한사항

• n은 3 이상 250,000 이하입니다.
  • edges의 행의 개수는 n-1 입니다.
  • edges의 각 행은 [v1, v2] 2개의 정수로 이루어져 있으며, 이는 v1번 정점과 v2번 정점 사이에 간선이 있음을 의미합니다.
  • v1, v2는 각각 1 이상 n 이하입니다.
  • v1, v2는 다른 수입니다.
  • 입력으로 주어지는 그래프는 항상 트리입니다.

입출력 예
n edges result
4 [[1,2],[2,3],[3,4]] 2
5 [[1,5],[2,5],[3,5],[4,5]] 2

2) 문제 분석 및 풀이

1) 설계, 분석

2) 풀이

#include <vector>
#include <queue>
using namespace std;

// BFS 결과: (가장 먼 거리, 가장 먼 노드 목록)
pair<int, vector<int>> bfs(int start, const vector<vector<int>>& adj, int n) {
    vector<bool> vis(n+1, false);
    queue<pair<int,int>> q;
    q.push({start, 0});
    vis[start] = true;

    while (!q.empty()) {
        auto [u, d] = q.front(); q.pop();
        if (d > maxDist) {
            maxDist = d;
            farthest.clear();
            farthest.push_back(u);
        } else if (d == maxDist) {
            farthest.push_back(u);
        }
        for (int v : adj[u]) {
            if (!vis[v]) {
                vis[v] = true;
                q.push({v, d + 1});
            }
        }
    }
    return {maxDist, farthest};
}

int solution(int n, vector<vector<int>> edges) 
{
    vector<vector<int>> adj(n + 1);
    for (auto& e : edges) 
    {
        adj[e[0]].push_back(e[1]);
        adj[e[1]].push_back(e[0]);
    }

    auto [d1, far1] = bfs(1, adj, n);
    auto [d2, far2] = bfs(far1[0], adj, n);

    if (far2.size() > 1) return d2;  
    auto [d3, far3] = bfs(far2[0], adj, n);
    if (far3.size() > 1) return d3;  
    return d3 - 1;                   
}

3. 쿼드압축 후 개수 세기

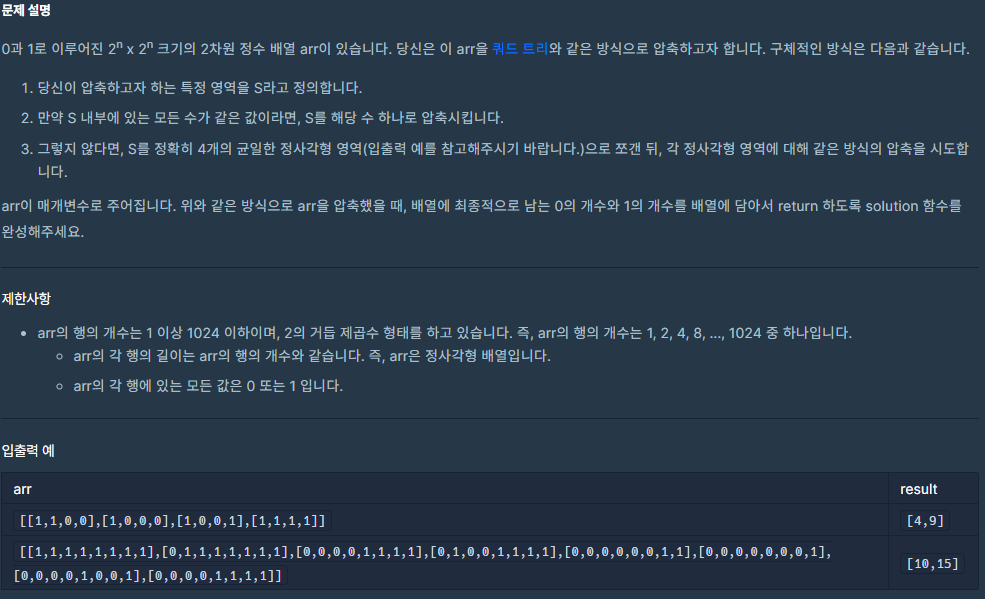
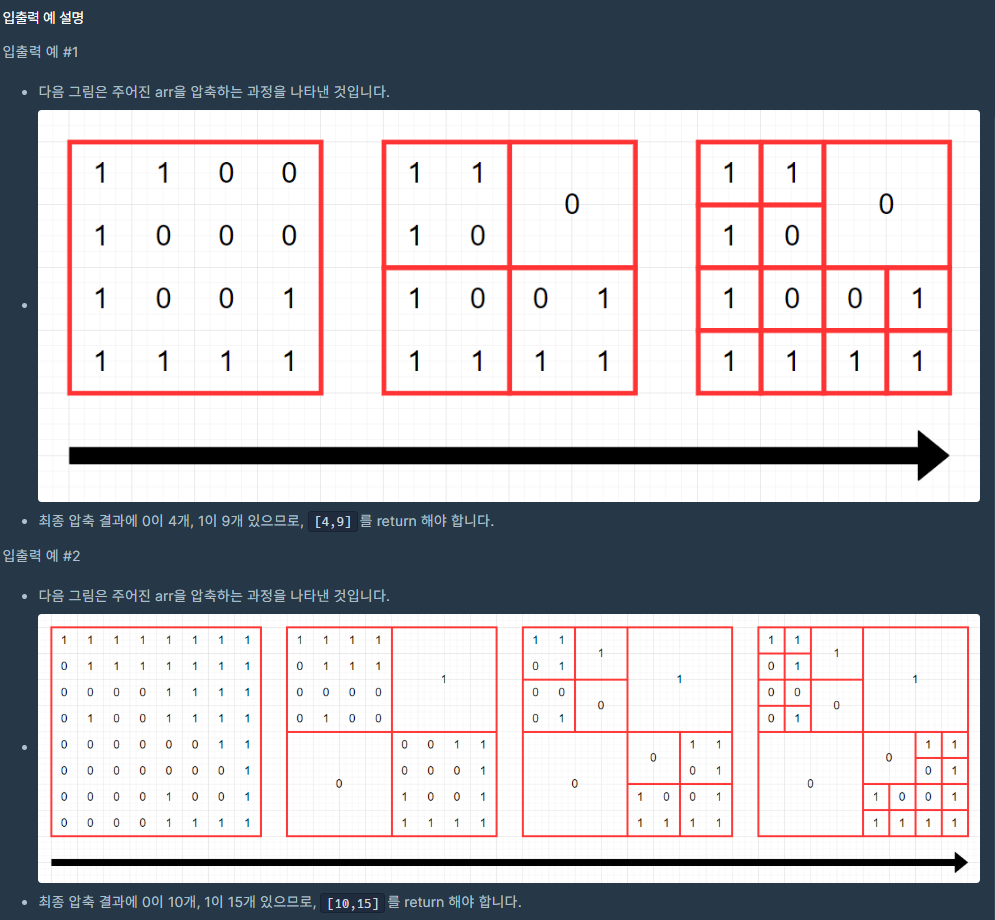
1) 문제

2) 문제 분석 및 풀이

1) 설계, 분석

$N \le 1024$ 이므로 $O(N^3)$ 이하의 알고리즘으로 해결 해야함

• 재귀 기반의 DFS로 해결
• 현재 정사각형 격자의 합을 구한다.
  • 합이 0 -> 0으로 압축
  • 합이 정사각형의 넓이 -> 1로 압축
  • 이외의 경우 구역을 4개로 나누고 각 구역마다 같은 과정 반복

$O(N^2logN)$
2차원 배열의 prifix sum을 구하면 $O(N^2)$까지 최적화 가능

2) 풀이

#include <string>
#include <vector>

using namespace std;

vector<int> answer(2);

void QuadTreeCompression(int x, int y, int len, vector<vector<int>>& arr)
{
    int sum = 0;
    for (int i=x; i<x+len; i++)
    {
        for (int j=y; j<y+len; j++)
        {
            sum+=arr[i][j];
        }
    }
    
    if (sum == 0) 
    {
        answer[0]++;
        return;
    }
    
    if (sum == len * len) 
    {
        answer[1]++;
        return;
    }
    
    QuadTreeCompression(x ,y ,len/2, arr);
    QuadTreeCompression(x + len/2, y, len/2, arr);
    QuadTreeCompression(x, y+len/2, len/2, arr);
    QuadTreeCompression(x+len/2, y+len/2, len/2, arr);
    
}

vector<int> solution(vector<vector<int>> arr) 
{
    QuadTreeCompression(0,0,arr.size(), arr);
    return answer;
}

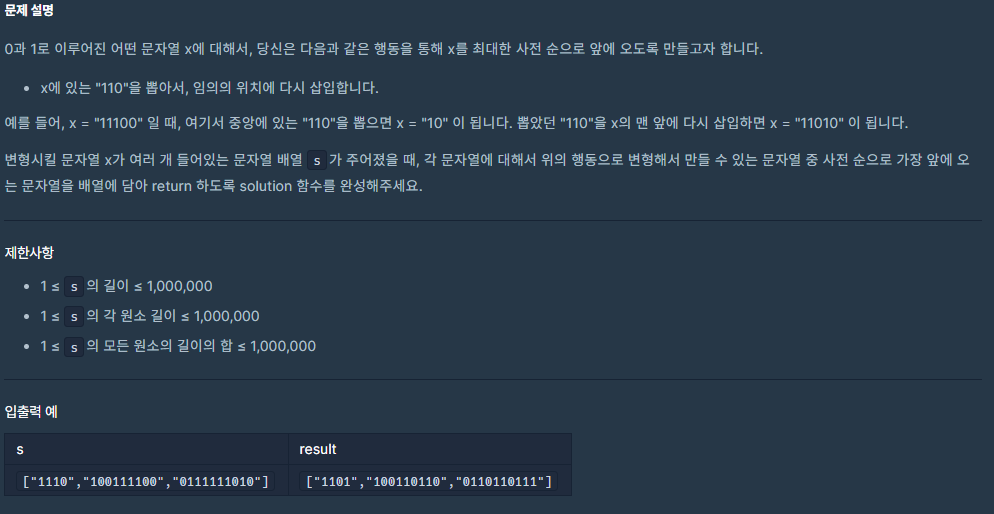
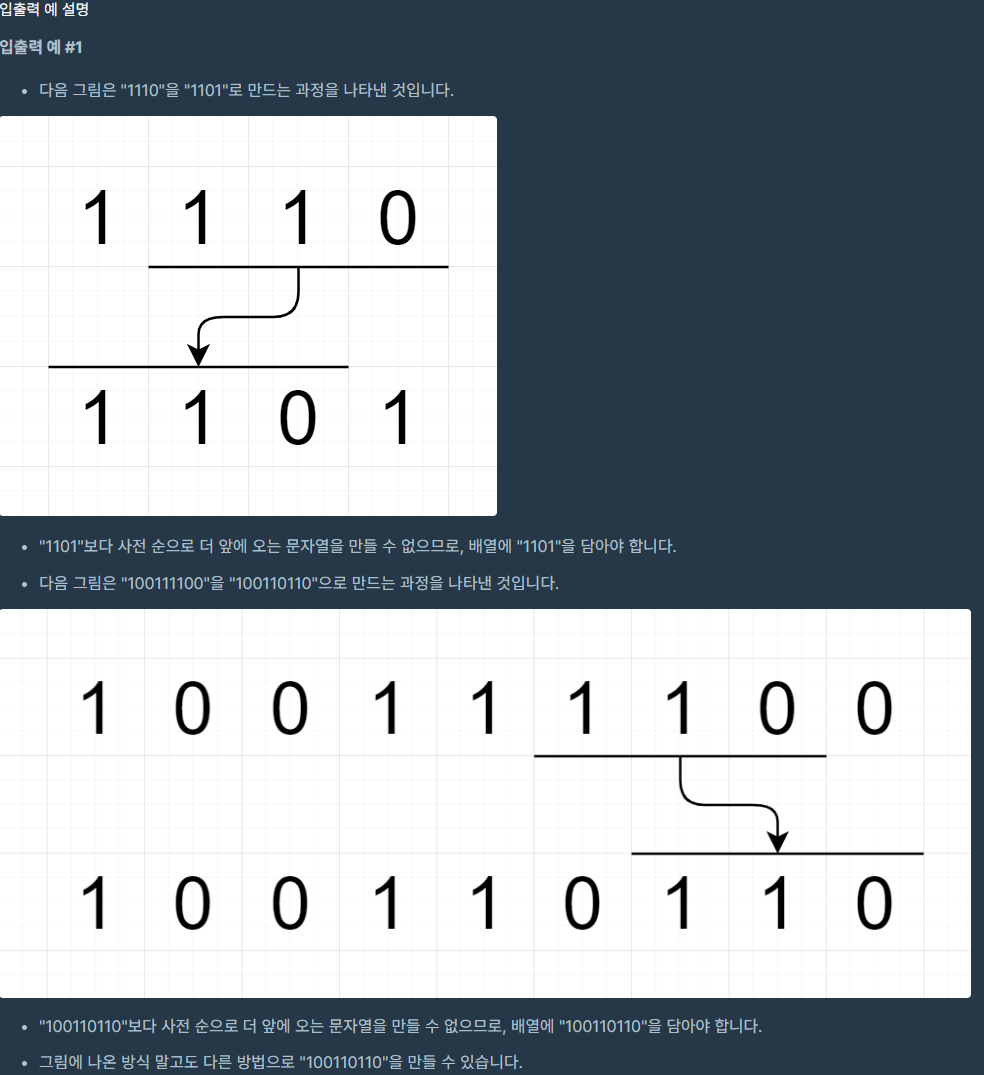
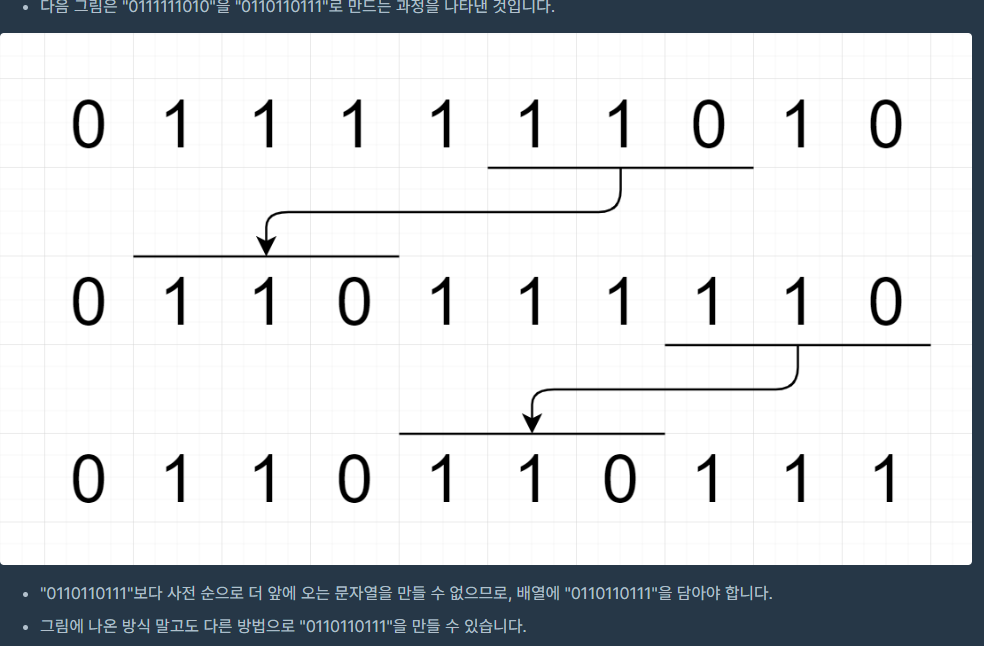
4. 110 옮기기

1) 문제

2) 문제 분석 및 풀이

1) 설계, 분석

$N \le 1,000,000$ 이므로 $O(NlogN)$ 이하의 알고리즘으로 해결 해야함

나의 풀이

• 다음을 반복한다
  • 문자열에서 110을 찾는다
    • 110을 기준으로 오른쪽에 0 이 있으면 0이 끝나는 지점 뒤로 110을 옮긴다.
    • 오른쪽에 0이 없고 왼쪽에 1이 있으면 1이 끝나는 지점 앞에 110 삽입

예제는 잘 해결되었는데, 제출하니 와장창... 중간에 예외적인 경우가 많았던 모양
$O(N^2)$ 이다보니 시간 초과도 발생

실제 풀이

• 공식 해설을 살펴보면 놀랍게도 탐욕법을 활용한 문제라고 한다.
• 왜 그리디?
  • 문자열을 훑으며 110이 있으면 바로 제거
    • 이 선택이 다음 선택에 영향을 주지 않음
    • 110을 제거 한다고 다른 110을 제거 못하는 상황은 없음
  • 제거된 110들을 111앞에 삽입, 없으면 맨뒤
    • 3글자 숫자들을 보면 000 001 010 011 100 101 110 111
    • 위 숫자들중 110은 111 다음으로 큰 수 110의 위치는 111 앞이 최선
    • 정확히 말하면 연속된 1의 앞에 삽입
    • = 마지막 0의 뒤에 삽입
• 스택을 사용해 110 제거
• 최초로 발견한 111 앞에 110들 삽입

2) 풀이

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

vector<string> solution(vector<string> s) 
{
    vector<string> answer;
    for (int i=0; i<s.size(); i++)
    {
        string str;
        int cnt=0;
        for (auto& c : s[i])
        {
            str.push_back(c);
            // 스태의 크기가 3보다 크고 가장 최근에 110이 삽입된 상태라면
            if (str.size() >= 3 && str.substr(str.size()-3) == "110")
            {
                // 110개수를 늘리고 110 지우기
                cnt++;
                for (int i=0; i<3; i++)
                    str.pop_back();
            }
            
        }
        
        // 가장 마지막 0의 뒤 (연속된 1의 앞)
        int index = 0;
        for(int i=str.size()-1; i>=0; i--)
        {
            if (str[i] == '0')
            {
                index = i+1;
                break;
            }
        }

        // 해당 위치에 110들 삽입
        string left = str.substr(0,index);
        string right = str.substr(index);
        str = "";
        while(cnt)
        {
            str += "110";
            cnt--;
        }
        answer.push_back(left + str + right);
    }
    return answer;
}