Ch 5-2. 벨만-포드 최단 경로 알고리즘

• 다익스트라 : 음수 가중치 가진 그래프에서 최단 경로 못 찾음
  - 그리디 알고리즘은 한번 확정된 해에 대해 수정하지 않기 때문 -> 확정된점에 대한 간선 완화 수행 안 함

• 그리디 쓰지 말고, 확정된 점 & 미확정된 점으로 구분 짓지 않고 간선완화해야 함

• 음수 사이클 : 사이클 상의 간선의 가중치의 합이 음수인 사이클
  

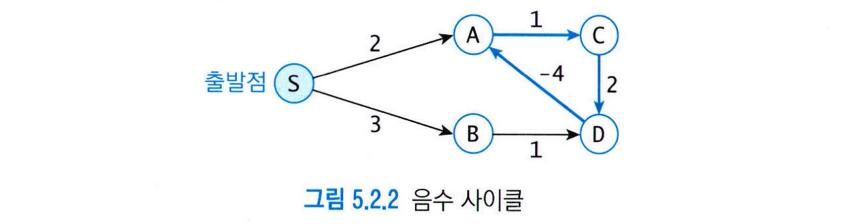
• 경로상에서 음수 사이클 반복할수록 거리 더 짧아짐
  => 최단 경로 찾는 입력 그래프엔 음수 사이클이 없다고 가정

• 출발점에서 시작해 좌->우로 간선 완화를 단계적으로 수행하여 직전 점의 결과가 다음 점에 연속하여 반영돼도록 해야함

💡 선형 그래프에서 최단 경로 찾는 방식을 일반적인 그래프에 어떻게 적용할까?

➡️ 그래프의 출발점에서 간선 수만 카운트하여 가장 멀리 떨어져 있는 점을 서로 반대 방향을 잡아 당겨보자!

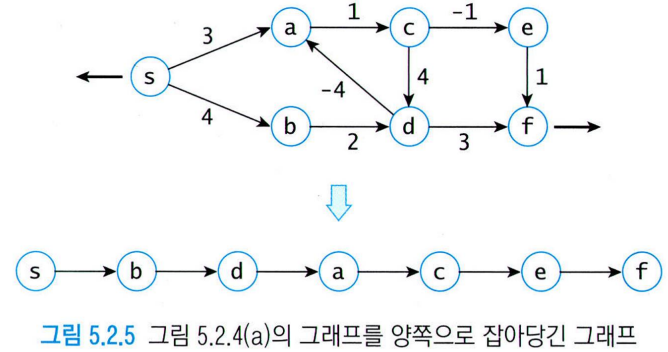
💡 간선 완화를 1회 시도할 때마다 어떤 점들이 간선 완화에 참여해야할까?

선형 아닌 그래프는 점 구분 어려움
➡️ 모든 점에 대해 간선완화 시도!

📌 Bellman-Ford 최단 경로 알고리즘

정점 : 0,~n-1, 알고리즘 종료 후 D[i]=출발점 s에서 점 i까지의 최단 거리

1. D를 inf로 초기화
   단 D[s]=0, s : 출발점
2. 다음 과정을(최대) n-1회 수행
   : 각 간선<i,j>에 대해 간선 완화 시도

💡 간선 완화 방법 : 다익스트라 알고리즘과 동일

• P[j] : 누구 덕분에 거리가 단축되었는지

if D[j] > (D[i] + 간선 <i,j>의 가중치):
	D[j] = D[i] + 간선 <i,j>의 가중치	# 간선 완화
    previous[j] = i	# 정점 i가 j의 직전 정점으로 업데이트

📌 벨만-포드 알고리즘이 왜 "작은 것부터 풀어보기" 방식일까?

• 시작점 자체가 가장 작은 문제
• 각 n-1개의 정점의 관점에서작은 문제를 살펴보면,
  직전 점까지의 해를 찾은 후에야 해당 점까지의 최단 경로가 결정됨
• 출발점 -> 도착점까지의 경로가 가장 긴 증가 순서의 그래프와 유사함
  ➡️ 각 정점의 관점에서 간선 완화가 수행되어 도착점까지 전파되는 과정 자체가 작은 것부터 해결하는 방식임

📌 수행시간

각 간선 <i,j>에 대해 간선 완화를 n-1회 시도함

• 간선 수가 m이면,
  수행시간 = (n-1) x O(m) = O(mn)
• 그래프를 인접 행렬로 사용하면 O(n^3)