Ch 5-1. 가장 긴 증가 순서

📌 동적 계획 알고리즘

작은 문제 = "부분 문제"

• 원래 주어진 문제와 같은 문제
• 작은 문제의 입력 = 원래 문제 입력의 일부분임

숫자가 일렬로 나열됐을 때 가장 긴 증가 순서 찾기

모든 숫자 조합으로 증가순서 만들기

(2^n) -1 가지

📌 그래프로 해결

• 가장 긴 증가 순서 = 그래프에서 가장 긴 경로
  각 점에서 오른쪽에 위치한 점에 대해 자신보다 큰 숫자를 가진 점을 간선으로 연결

• 그래프의 간선 방향 : 좌 -> 우

• 가장 왼쪽 점부터 좌 -> 우로 1개씩 각 점에 도달하는 최장 경로 찾음

💡 알고리즘

1. 주어진 숫자들로 그래프 만들기
2. 가장 왼쪽 정점으로부터 하나씩 차례로

• 정점으로 들어오는 간선들 중 가장 긴 경로 길이에 +1 => 각 경로의 길이 계산

3. 각 정점의 경로 길이 중 가장 긴 것을 반환

예제

1. 가장 왼쪽 점에 들어오는 간선 없음
   ➡️ 경로 길이 1
   *) 회색 원 안의 점들은 지금 단계에선 무시

2. 2번째 점으로 들어오는 간선 없음
   ➡️ 경로 길이 1

3. 3번째 점으론 2개의 간선 들어옴
   ➡️ 경로 길이 1+1=2

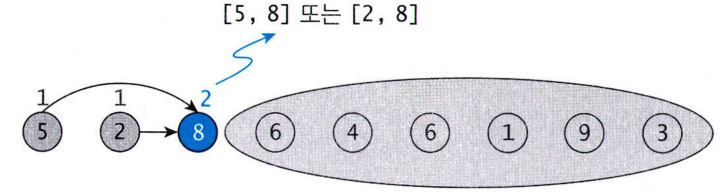
4. 4,5번째 점으론 들어오는 간선들의 경로 길이가 각각 1임
   ➡️ 경로 길이 1+1=2

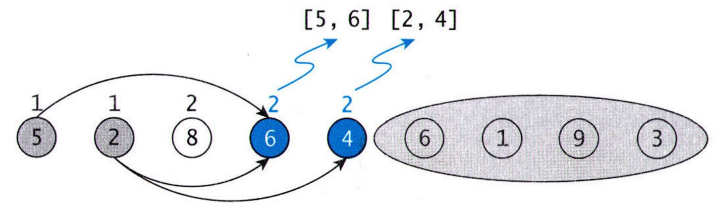
5. 6번째 점으론 들어오는 간선 중 가장 길이가 긴 경로가 2
   ➡️ 경로 길이 2+1=3

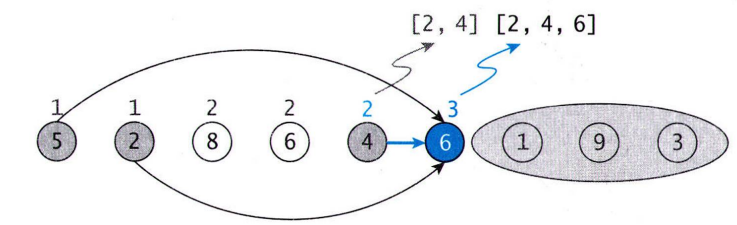
6. 7번째 점(1이어서)으론 들어오는 간선 없음

7. 8번째 점으론 들어오는 간선 중 가장 길이가 긴 경로가 6으로부터 온 거임 ; 3
   ➡️ 경로 길이 3+1=4

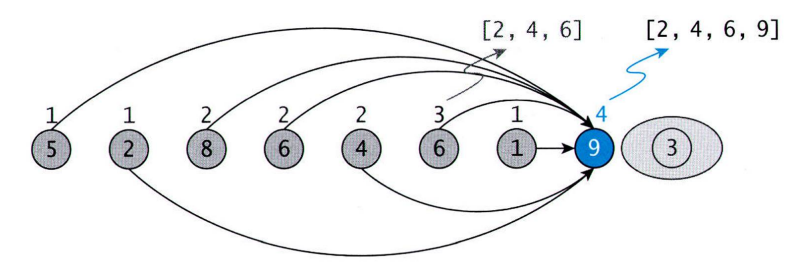
8. 마지막 점으론 경로 1인 간선만 들어옴
   ➡️ 경로 길이 1+1=2

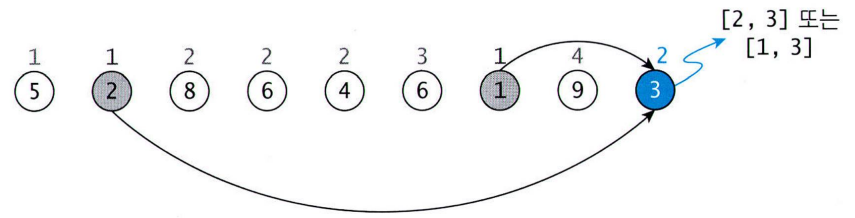
=> 가장 긴 증가 순서의 길이는 4

📌 수행시간

1. 그래프 만들기 : 최대 간선 수 n(n-1)/2
   => O(n^2) 걸림
2. 좌->우로 각 점으로 들어오는 간선에 대해 연산 수행 : 총연산량 = 그래프의 간선 수(m개)
   => O(m)

➡️ 총 수행시간 : O(n^2) + O(m) = O(n^2)