
1. Stable Matching Algorithm (안정적인 결혼 알고리즘)
- Gale-Shapley 알고리즘 (게일-섀플리 알고리즘, GSA)
- N명의 남성 & N명의 여성의 선호도를 기반으로 N개의 쌍으로 엮어줌
- 로직에서 선택권이 여성에게 있어서 여성에게 유리한 알고리즘으로 보일 수 있지만,
실제로 수학적인 증명과정을 거치면 고백을 하는 남성에게 더 유리함
📌 일반적인 추천 알고리즘과의 차이점
기본적으로 추천 시스템은 1:N임
ex) 넷플릭스 영화 추천, 쇼핑몰 연관 상품 추천, 유튜브 영상 추천 알고리즘 등
-> 특정 영상들에 쏠리게 되고, 인기가 많은 컨텐츠에 더 많은 사람들이 몰리게 됨
but 게일-섀플리 알고리즘은 남녀가 어떻게 만나야 최적의 짝이 될 수 있는지에서 비롯된 알고리즘이기 때문에 일대다 개념이 사라지고, 최적의 매칭을 생각해야함
📌 활용 사례
- 의대생과 병원을 이어주는 레지던티 지원 프로그램
- 장기기증 매칭 시스템
- 데이팅 앱 매칭
...
📌 노벨 경제학상 수상
이후 앨빈 로스가 이 알고리즘을 현실의 많은 문제들에 적용하여, 2012년 노벨 경제학상을 받게된다.
2. logic
🌿 공식 문서에서 수학적으로 표현된 알고리즘 참고
공식 문서
- N명의 남성 & N명의 여성은 각자 가장 마음에 드는 상대방부터 차례대로 적은 선호도 리스트 가지고 있음
<전체 로직>
1. 짝이 없는 남성은 자신이 가장 선호하는 여성에게 가서 고백을 함
2. 해당 여성도 짝이 없는 상태이면, 남성의 고백을 받아줌
이미 짝이 있는 상태라면, 고백한 남성과 이미 사귀고 있는 남성 중 선호도가 더 높은 사람과 짝을 맺음
3. 1,2번의 과정을 모든 남성이 각자의 짝을 맺을 때까지 반복함
4. 짝이 없는 남성이 1명도 없다면 종료함
🌿 예시
남성
서율 : 무덕, 진초연, 허윤옥
장욱 : 무덕, 진초연, 허윤옥
박당구 : 진초연, 무덕, 허윤옥
여성
무덕 : 박당구, 서율, 장욱
진초연 : 장욱, 박당구, 서율
허윤옥 : 서율, 장욱, 박당구
🌿 1 ROUND
1) 남성들이 1순위로 선택한 여성한테 고백한다.
무덕 : 장욱, 서율
진초연 : 박당구
허윤옥 : 없음
2) 여성은 고백한 남성들 중 가장 마음에 드는 짝을 선택한다.
무덕 : 서율
진초연 : 박당구
허윤옥 : 없음
장욱 : 없음
1라운드가 끝나면 위와 같은 결과가 나온다.
두 커플이 생성됐지만 한 커플이 만들어지지 않았으니 2라운드를 진행한다.
🌿 2 ROUND
3) 선택 받지 못한 장욱이 자신이 2순위로 선택한 진초연에게 고백한다.
-> 진초연은 이미 박당구와 짝을 이뤘지만, 1순위가 장욱이었기 때문에 장욱을 짝으로 선택한다.
무덕 : 서율
진초연 : 장욱
허윤옥 : 없음
박당구 : 없음
박당구가 다음 라운드에서 선택을 해야한다.
🌿 3 ROUND
4) 박당구가 자신이 2순위로 선택한 무덕한테 고백한다.
-> 무덕은 이미 서율과 짝을 이뤘지만, 1순위가 박당구였기 때문에 박당구를 짝으로 선택한다.
무덕 : 박당구
진초연 : 장욱
허윤옥 : 없음
서율 : 없음
🌿 4 ROUND
5) 서율이 자신이 2순위로 선택한 진초연한테 고백한다.
-> 진초연은 이미 자신의 1순위인 장욱과 짝이 됐기 때문에 서율의 고백을 거절한다.
6) 서율이 자신이 3순위로 선택한 허윤옥한테 고백하여 짝이 된다.
최종 커플
무덕 : 박당구
진초연 : 장욱
허윤옥 : 서율
🧐 과연 이 선택이 최선일까?
이 매칭 알고리즘은 단순히 커플을 매칭하는 것에서 끝나지 않고, 이후의 상황까지 고려한다!
무덕이와 박당구 입장에서 무덕이는 이미 가장 마음에 드는 남성을 선택했으므로 다른 남성과 바람이 날리 없고, 박당구에게는 무덕이가 2순위이지만 이미 박당구는 자신의 1순위였던 진초연에게 버림 받았기 때문에 무덕이와 박당구는 최적화가 된 커플이다.
=> 커플 성사 이후의 만족도까지 고려하면, 이렇게 라운드를 여러 차례 실행하는 방식이 가장 이상적이다!
3. python으로 구현
📌 사용한 numpy 함수
1) numpy.binary_repr(num, width=None)
- 십진수를 이진수로 변환하여 출력해줌
- num에는 변환할 십진수, width에는 몇 비트로 표현할 것인지 입력
ex)
np.binary_repr(3) #'11'
np.binary_repr(3, width=3) #'011'
np.binary_repr(3, width=4) #'0011'2) numpy.vstack
- 배열을 세로로 결합할 때 사용
ex)
import numpy as np
# 배열 준비
a = np.arange(10).reshape(2,5)
b = np.arange(15).reshape(3,5)
# 배열과 배열 결합
c = np.vstack((a,b))
3) np.argsort
크기가 작은 값부터 순서대로 인덱스 반환
4) numpy array의 곱연산
- @ : 행렬곱
- .dot : 내적
- : 스칼라곱 (브로드캐스팅)
5) python matching 패키지
-
패키지 링크
matching 1.4 -
패키지 독스
Matching’s documentation
💡 dictionary 형태로 game 생성하는 방법
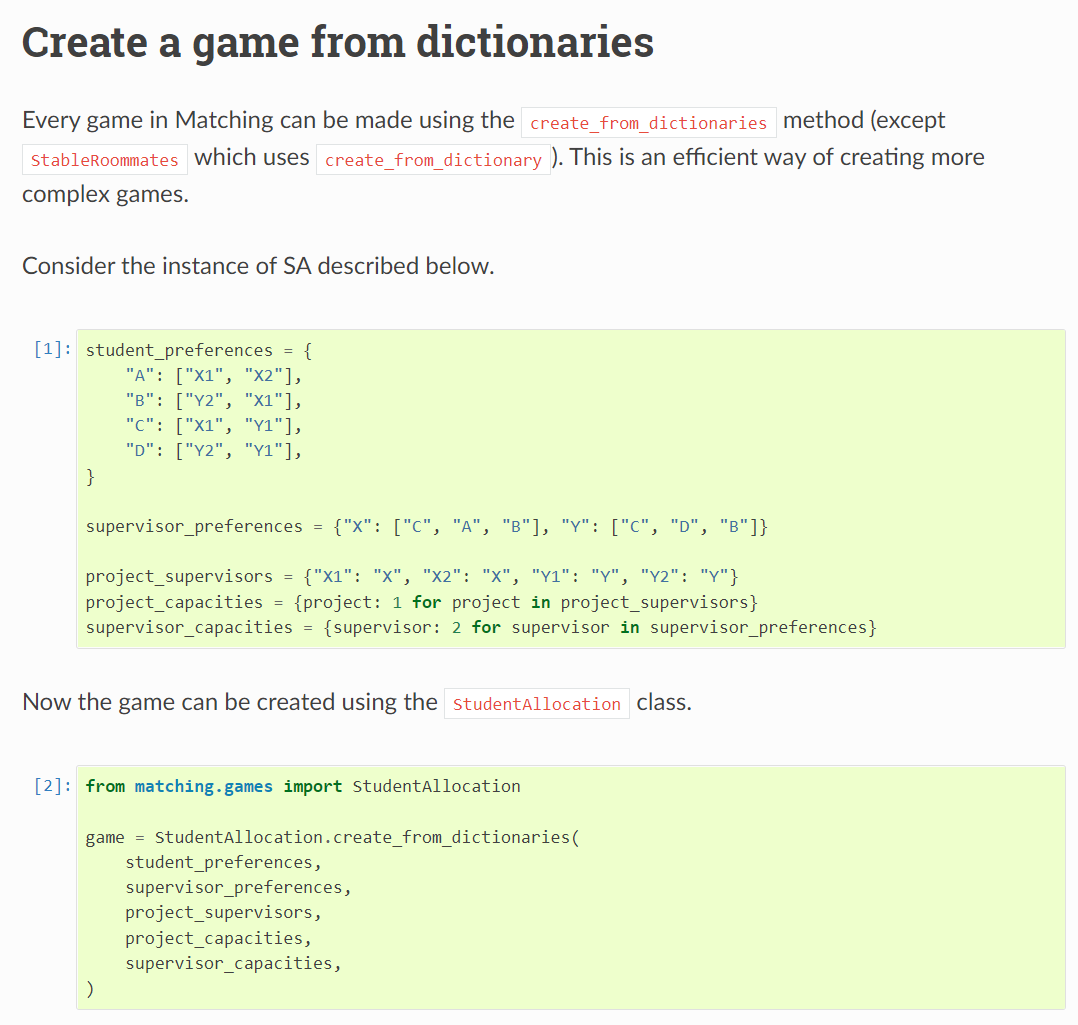
💡 사용 코드
from matching.games import StableMarriage
...
game.solve()
game.check_validity()
game.check_stability()📌 dataframe 생성 및 수정
- 궁합 행렬을 생성하여 여성의 선호도를 기준으로 가장 궁합이 안 맞는 남성 탈락 시킴
1) 궁합 행렬 생성

2) 남자를 기준으로 여자와의 궁합의 최대값을 뽑아서 새로 생성한 MaxPreference 컬럼에 저장

3) MaxPreference에서 최소값을 가진 행(남성)을 삭제

4) MaxPreference 컬럼 삭제

- 남성의 선호도를 기준으로 여성과의 궁합이 높은 순으로 dictionary 형태로 뽑음
{'m1': ['f1', 'f3', 'f2'], 'm3': ['f3', 'f2', 'f1'], 'm4': ['f1', 'f2', 'f3']}- 여성의 선호도를 기준으로 남성과의 궁합이 높은 순으로 dictionary 형태로 뽑음
{'f1': ['m4', 'm3', 'm1'], 'f2': ['m3', 'm4', 'm1'], 'f3': ['m3', 'm4', 'm1']}- 두 dictionary를 StableMarriage.create_from_dictionaries() 메서드에 넣고 매칭시킴
{m1: f2, m3: f3, m4: f1}- Check the status of a matching : validity & stability 확인
boolean 타입으로 출력됨
둘다 True일 시 통과
