다익스트라(Dijkstra) 알고리즘

1. 다익스트라 알고리즘

• 그래프 상에서 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘 중 하나
  - 이외에도 최단경로 구하는 알고리즘 : 벨만-포드 알고리즘, 프로이드 워샬 알고리즘 등
• 도착 정점 뿐만 아니라 다른 모든 정점까지 최단 경로로 방문하며 각 정점까지의 최단 경로를 모두 찾게 됨 (= 매번 최단 경로의 정점을 선택해 탐색을 반복하는 것)

2. 동작 단계

1) 출발 노드와 도착 노드를 설정
2) 최단 거리 테이블을 초기화
3) 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고,
방문하지 않은 노드 중 가중치 값이 가장 작은 노드 선택 -> 그 노드를 방문 처리
4) 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(=가중치)를 계산해 최단 거리 테이블 업데이트
5) 3,4번 과정 반복

🌿 최단 거리 테이블

• N+1 크기의 1차원 배열
• N개 노드까지 오는 데에 필요한 최단 거리를 기록함
• N+1 크기의 배열 선언 후, 초기값을 무한대(INF)로 초기화

🌿 노드 방문 여부 체크 배열

• 최단 거리 테이블과 크기 같음
• 초기값 False로 초기화

3. 예시

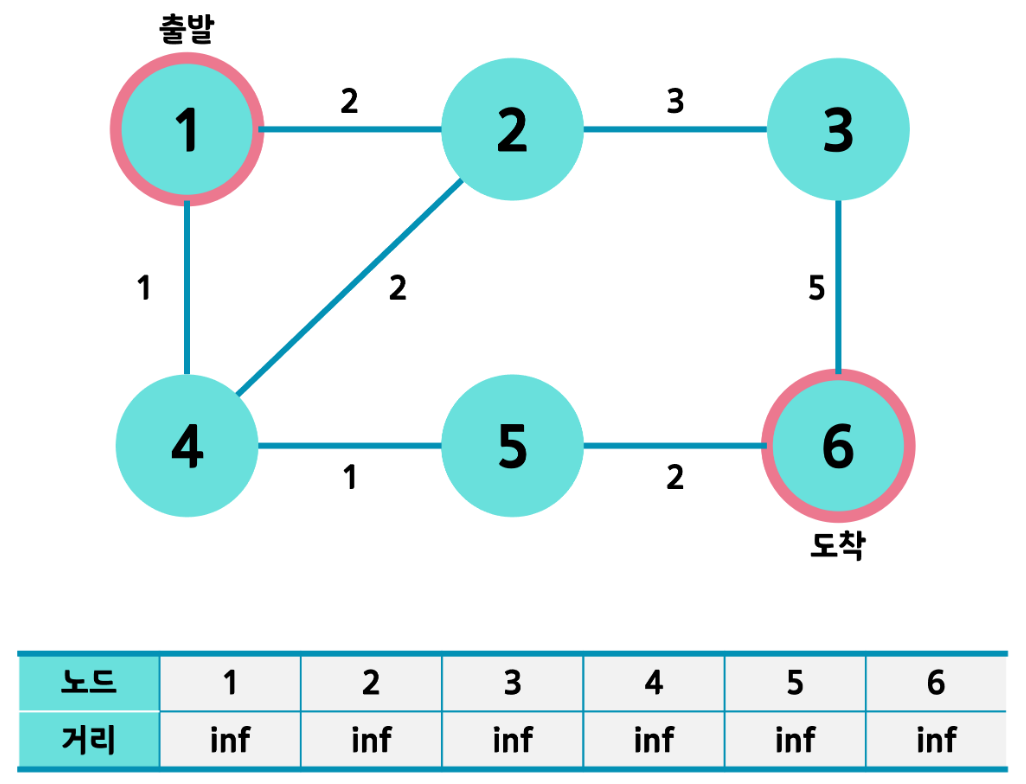
1) 출발 노드 : 1번, 도착 노드 : 6번로 설정
최단 거리 테이블의 초기값을 무한대(INF)로 초기화

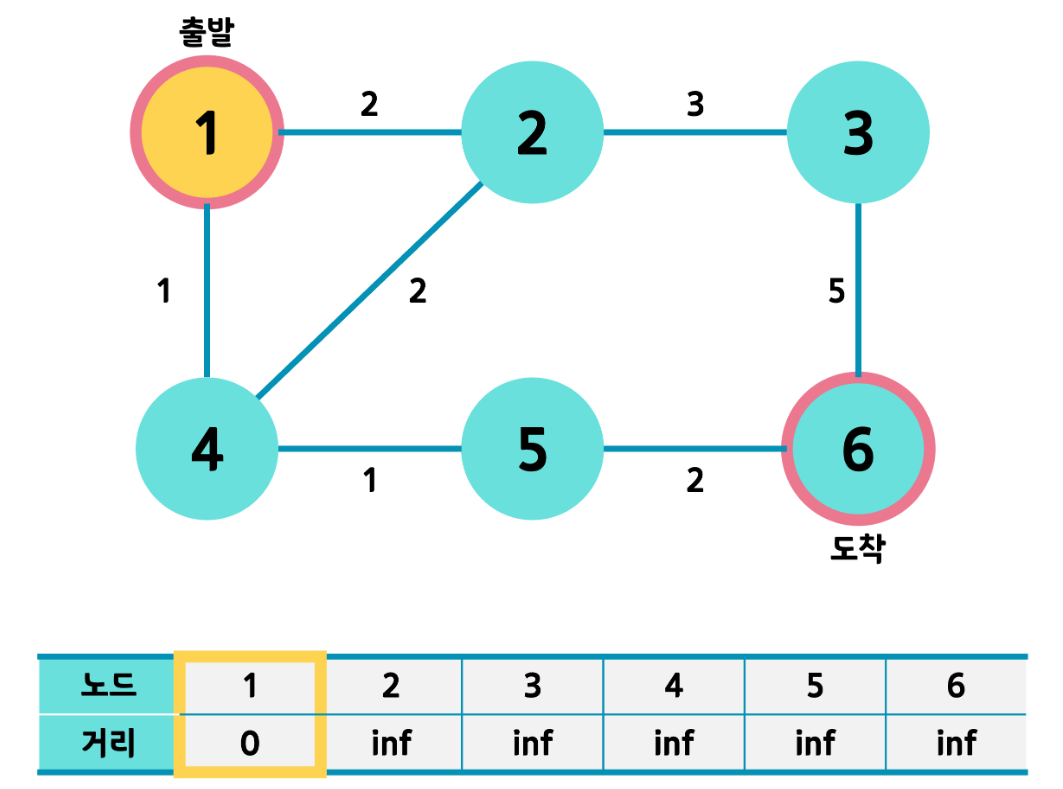
2) 출발 노드 먼저 선택 후 거리를 0으로 설정

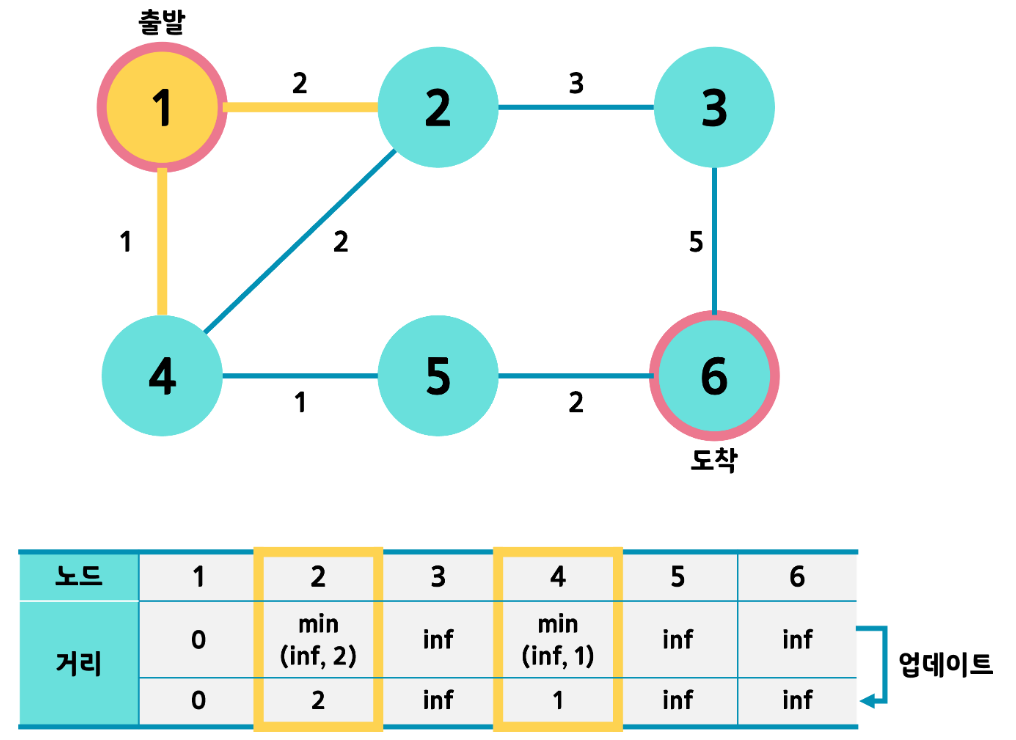
3) 2,4중 선택

4. 구현

🧐 고려사항

방문하지 않은 노드를 다룰 때

• 순차 탐색을 할지
• 우선순위 큐를 쓸지
  에 따라 2가지 구현 방법이 있음

4.1. 순차 탐색 사용

• 노드 개수에 따라 탐색 시간 매우 오래 걸림 => 우선순위 큐 도입!

4.2. 우선순위 큐 사용