ch 5-4. 합이 최대 K되는 숫자

📌 새로운 스케줄링 문제

• 각 동아리가 미팅에 필요한 시간만 제시
• 1개의 미팅룸에 특정 시간 동안 가능한 한 미팅룸이 비어 있지 않도록 동아리들을 배정
• 선택된 동아리 수 or 동아리의 미팅 순서는 중요 X

📌 합이 '최대' K 되는 숫자 문제

• 집합의 숫자들 = 물건의 무게
• K = 배낭의 용량
• '각 물건의 가치 = 무게' 인 특수한 형태의 배낭 문제

• 최적화 부분 집합의 합
• n개의 숫자에 대해 합이 최대 K가 되는 숫자들을 찾는 문제
• 주어진 숫자들 중 합이 K 되는 숫자들 없으면 그 합이 K에 가장 가까운 숫자들을 찾음

📌 (작은) 부분 문제

1. 물건을 1개씩 늘려가며 부분 문제의 크기를 증가시킴
2. 트럭의 용량을 1부터 K까지 1씩 증가시키어 부분 문제의 크기를 증가시킴

📌 알고리즘

1. 물건을 차례로 하나씩 결정함

• 트럭 용량을 1씩 증가시키며 물건을 트럭에 싣는 것 vs 싣지 않는 것 중 뭐가 나은지 결정

2. return 마지막 물건에 대해 K일 때의 트럭에 실은 물건의 총량

📌 교재 예제

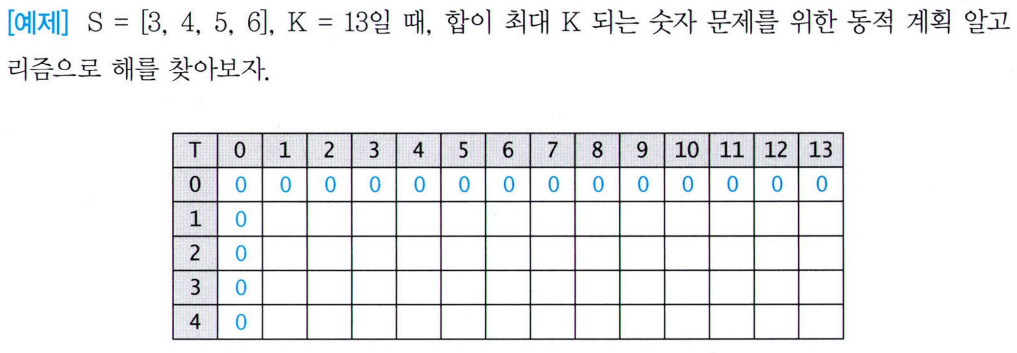
1. 1번째 물건 s1=3

• 트럭 용량을 1씩 증가시키면서 s1 트럭에 실음

2. 2번째 물건 s2=4

• s1도 함께 고려해서 유리한 경우로 표 채우기

3. n번째 물건까지 동일한 방법으로 반복!
   (배낭문제랑 비슷한듯?)

📌 수행 시간

• 물건 수 n
• 트럭 용량 K

➡️ 수행시간 : O(nK)
각각의 경우가 트럭에 물건을 실을지 말지 결정하는 거임 -> O(1) 시간만 걸림

• but K가 크지 않을 때만 동적 계획 알고리즘 쓰는게 좋음