ch 6-2. 여왕 말 문제

백트래킹 알고리즘

• 문제의 해 탐색하는 방식
• 백트래킹 : 해를 더 이상 얻지 못하면 바로 직전 상태로 되돌아가서 다른 것들 시도하며 해를 찾음
• 최적화 문제 & 결정 문제를 해결
  
• 결정문제 : 문제

여왕 말 - 8방향(상하좌우 및 대각선상)으로 이동 가능

여왕 말 문제 (n-Queens problem)

: Q가 같은 열 & 행 & 대각선상에 서로 놓이지 않도록 nxn 장기판에 n개의 Q를 배치하는 문제 (단 n>3)

여왕 말 백트래킹 알고리즘

1. Q를 (0,0)부터 놓기 시작하여 다음 말을 서로 위협하지 않도록 배치
2. 배치 불가능이면, 직전 말의 위치를 다음 칸으로 이동하여 다시 시도

• 다음 칸이 없는 경우엔 위층의 말을 다음 칸으로 이동
  즉, (n+1)번째 말을 놓을 수 없게 되면 n번째 말을 다음칸으로 이동시킨다는 뜻

예제

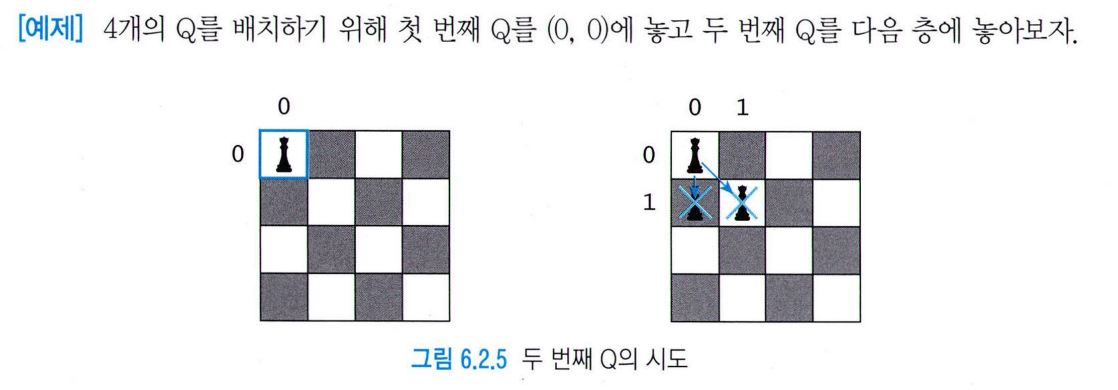
<1회차>

1. 1번째 Q (0,0)
2. 2번째 Q (1,2)

• 근데 3번째 Q를 놓을 수 없음
  

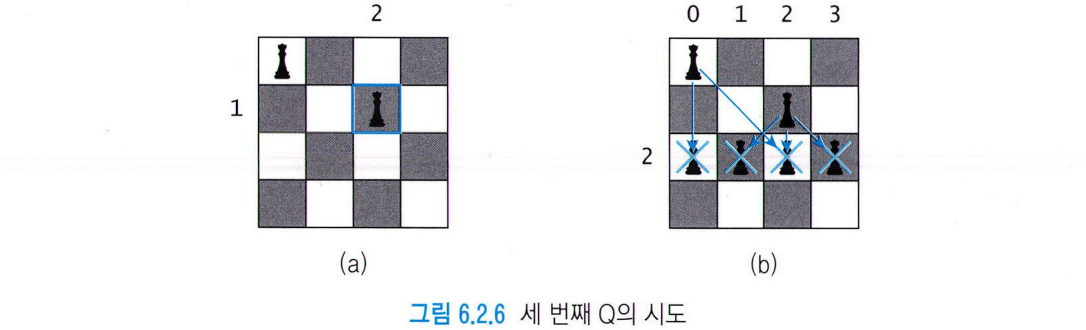
3. 2번째 Q (1,3)로 이동, 3번째 Q (2,1)
   

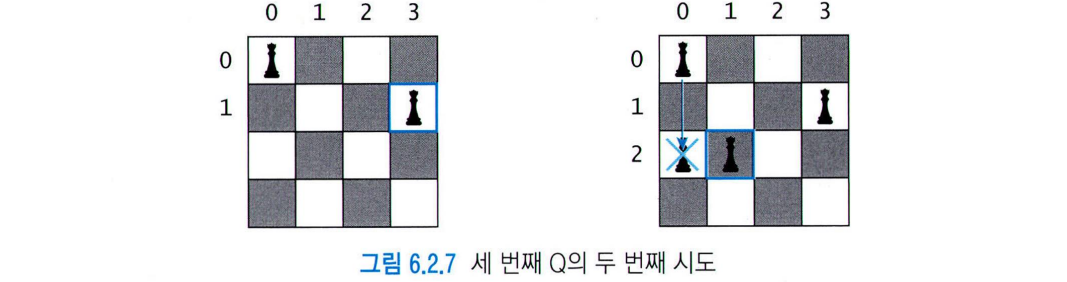
4. 마지막 Q 놓을 수 없음
   -> but 3번째 Q 이동 불가능

➡️ 백트래킹(거슬러 올라가자~)
2번째 Q는 더 이상 갈 수 있는 다음 칸 없음
또 백트래킹
1번째 Q를 (0,1)로 이동

<2회차>

1. 1번째 Q를 (0,1)로 이동
   

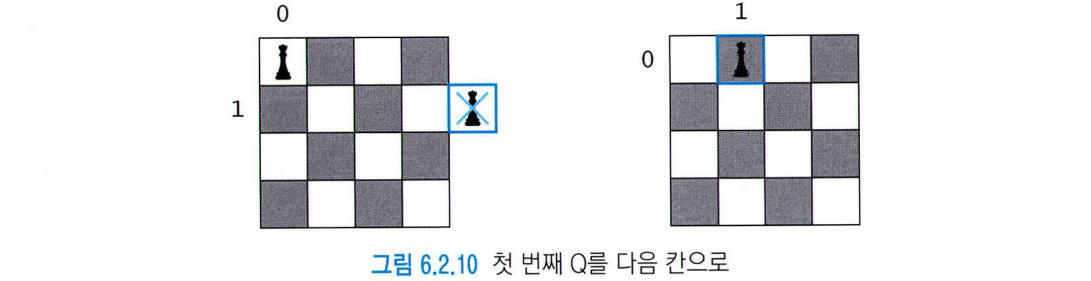
2. 2번째 Q (1,3)밖에 안 됨
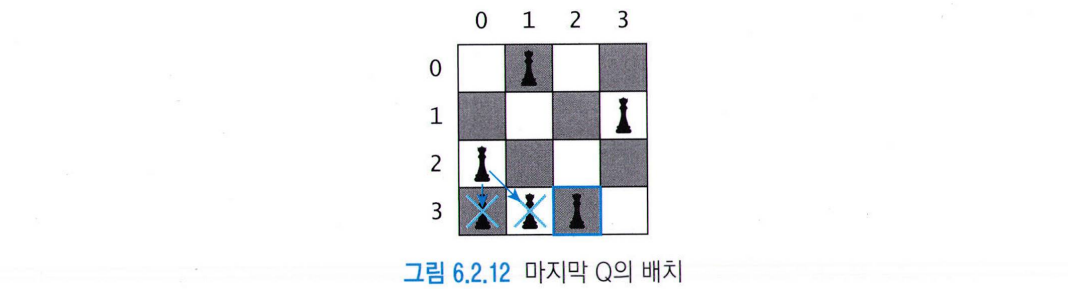
   3번째 Q (2,0)
   

3. 4번째 Q (3,2)
   

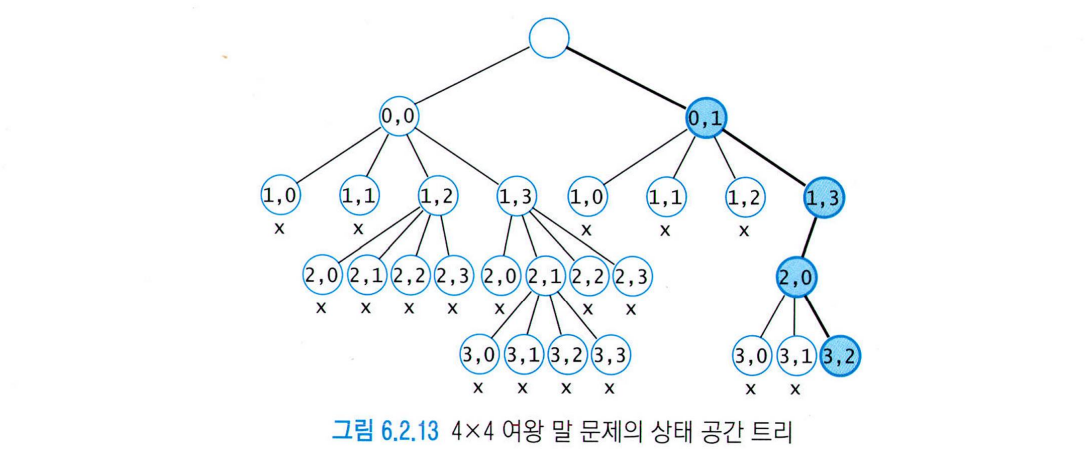
수행 시간

상태 공간 트리의 최대 크기 생각해보자!
상황 : n x n 체스판에서 n개의 Queen 놓기

• 각 노드가 n개의 자식 가짐
• 루트 제외한 높이가 n
  => 전체 노드 수 : 1+ n+n^2+...+n^n = O(n^n)

각 노드에서 8방향 검사해야함 -> O(n)시간
➡️ 총 수행시간 : O(n^n) x O(n) = O(n^(n+1))

여왕말 문제의 해가 존재하려면?

• n>3이면 n이 정수,실수인지 상관 없이 모든 경우애 해가 존재함