6. 되돌아가며 풀어보기

• 문제의 해를 탐색하는 방식

📌 백트래킹(Backtracking) 알고리즘

: 해를 찾는 과정에서 해를 더 이상 얻지 못하면 바로 직전 상태로 되돌아가서 다른 것을 시도하며 해를 찾음

• 최적화 문제 & 결정 문제 해결
• 결정 문제 : 문제에 대한 해의 존재 여부 - 해가 있다/없다 를 답하는 문제

1. DFS 깊이 우선 탐색으로 해를 탐색함

• 해가 있을 만한 곳 고려X 일정한 순서로 탐색함
• 단점 보완 -> 분기 한정 알고리즘!

2. 분기 한정(Branch-and-Bound) 알고리즘

• 한정 값(bound) 이용하여 한정 값이 가장 좋은 것부터 우선 탐색
  = "최선 우선(Best First)탐색"
• 최선 우선 탐색 : 해가 있을 만한 곳 우선 탐색
  ➡️ DFS보다 탐색 범위 줄여서 해 찾음

그래프 색칠하기

• 지도에서 인접 영역을 다른색으로 칠하기
• 그래프의 인접한 노드를 서로 다르게 색칠하는 문제
• 지도는 항상 그래프로 변환 가능

지도 -> 그래프 변환 방법

1. 지도의 각 영역에 대응되는 정점 만듦
2. 지도에서 인접하는 영역을 간선으로 이음

but, 모든 그래프를 지도로 만들 수는 없음!

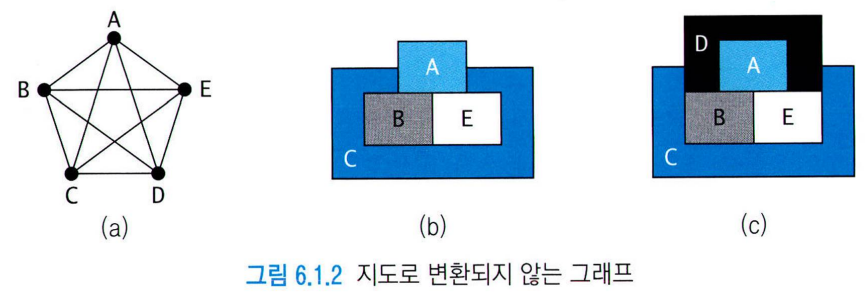
평면 그래프 : 항상 지도로 만들 수 있는 그래프

채색수 : 주어진 그래프를 색칠하는데 필요한 최소 색의 수

색칠하기 백트래킹 알고리즘

K : 색의 개수, n : 정점 개수

1. 정점 0을 하나의 색으로 칠함
2. 모든 점들이 색칠될 때까지
   다음 점이 이미 색칠된 점과 인접하면, 인접한 점의 색과 다른 색을 선택함

단, 주어진 K(=색의 수)에 대해 색칠 실패하면 K를 1증가 후, 처음부터 다시 알고리즘 수행

• 'x' 표시 : 인접한 노드의 색과 같아서 색칠 실패한 경우
  -> 그 아래에 남아있는 점들에 대해선 탐색 중단
• 가지치기 : 탐색을 중단하는 것
• 가지치기하면 부모 노드로 되돌아가서 다른 색 선택
  

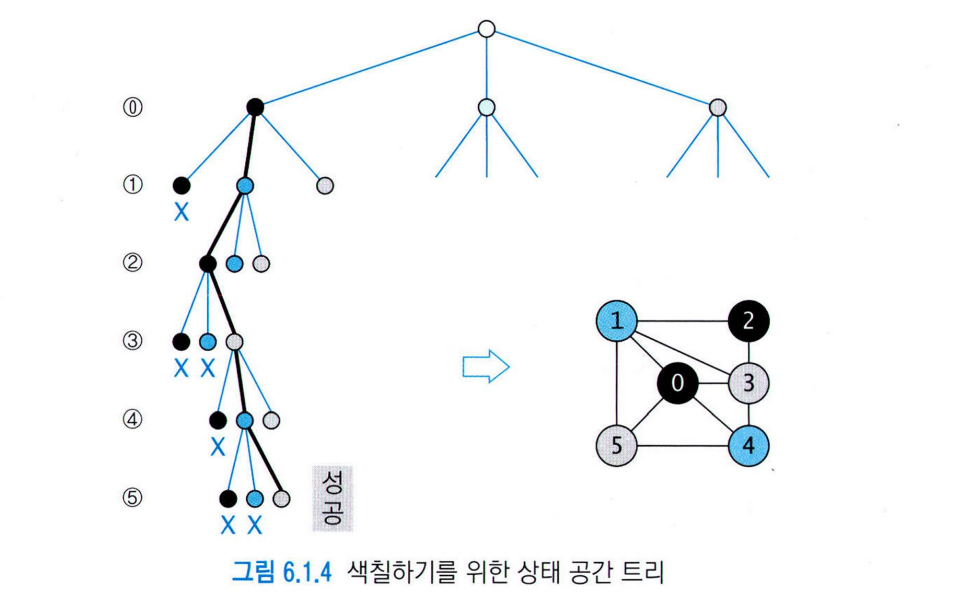
상태 공간 트리

• 루트 : 초기 상태 나타냄
• 각 레벨마다 정점을 차례로 할당하여 정점을 해당 색으로 색칠해봄
• 색칠 못하면 다음 색 시도
• 그래프 색칠 위해 실제로 상태 공간 트리 만들진 않음
• just 백트래킹 알고리즘이 해 찾는 과정 보여줌

상태 공간 트리의 최대 노드 수 계산

1번째 점의 색 경우의수 3가지 각 점에서 3개씩 노드 뻗어나감
3 (1부터 3^(n-1)까지 등비수열합)

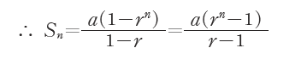
수행 시간

• 상태 공간 트리의 노드 수로 계산
• 루트 포함해 각 노드마다 K개의 자식 노드 있음
  ➡️ 총 노드 수 = 1 + K + K^2 + ... + K^n = O(K^n)
• 각 노드에선 그래프 색칠 유효한지 검사해야함
  ➡️ O(n) 시간

➡️ 둘이 곱해서 총 수행 시간 : O(nK^n)

다항식 시간에 색칠 가능한 그래프

1. 평면 그래프 : 어떤 간선도 서로 교차하지 않게 그릴 수 있는 그래프
   지도 변환한 그래프
2. 구간 그래프 : 구간 스케줄링 문제에서 동아리 = 정점, 두 동아리 미팅 시간이 겹치면 해당 정점 사이 간선 그려서 만든 그래프

• 미팅룸 수 = 구간 그래프의 K 채색수
• 같은 색의 정점(동아리)들을 동일한 미팅룸에 배정