ch 7-3. 통 채우기

통 채우기 문제

n개의 물건, 통의 용량이 C
주어진 모든 물건을 가장 적은 수의 통에 채우는 문제
(물건의 크기는 C보다 작음)

• 응용 : #대의 트럭에 물품 싣기, 작업 스케줄링, 부하 균형, 신문의 광고 배치 등

최적해; k = [모든 물건크기의 합 / C] 올림 한 값

통 채우기와 유사한 문제

• 용량 C인 1개의 통만 주어지고, 물건들을 통에 남는 부분 없이 채우는 문제 = 합이 K되는 숫자 문제
• 용량 C인 1개의 통만 주어지고, 물건들을 통에 최대한 채우는 문제 = 합이 최대 K 되는 숫자 문제
• 각 물건의 가치가 무게와 같은 입력의 배낭 문제

근사해 얻기 위한 그리디 알고리즘

1. 최초 적합(First Fit)
   :1번째 통부터 차례로 살펴보며, 가장 먼저 여유가 있는 통에 새 물건 넣음

2. 최선 적합 (Best Fit)
   : 새 물건 넣을 수 있는 통 중에서 남는 부분이 가장 적은 통에 새 물건 넣음

3. 최악 적합 (Worst Fit)
   : 새 물건 넣을 수 있는 통 중에서 남는 부분이 가장 큰 통에 새 물건 넣음

4. 다음 적합 (Best Fit)
   : 직전에 물건 넣은 통에 여유가 있으면 새 물건 넣음.
   넣을 수 없으면 새 통에 새 물건 넣음

수행 시간

• 최초, 최선, 최악 적합 : 새 물건 넣을 때마다 기존의 통들 살펴봐야함
  통의 수는 n을 안 넘으므로 수행시간 O(n^2)
• 다음 적합 : 새 물건에 대해 직전에 사용된 통만 살펴보기 땜에 수행시간 O(n)

근사 비율

모든 4가지 적합(최초, 최선, 최악, 다음)에서 근사 비율 2임

1) 최초, 최선, 최악 적합; 근사 비율 계산

• 최초, 최선, 최악 적합이 사용하는 통들 보면 2개 이상의 통이 1/2 이하로 채워져있는게 불가능
  => why? 각 3가지 방법에선 새 통을 안 쓰고, 물건들을 1/2 이하로 채워져있는 통 중 하나에 넣었을 것이기 때문
  

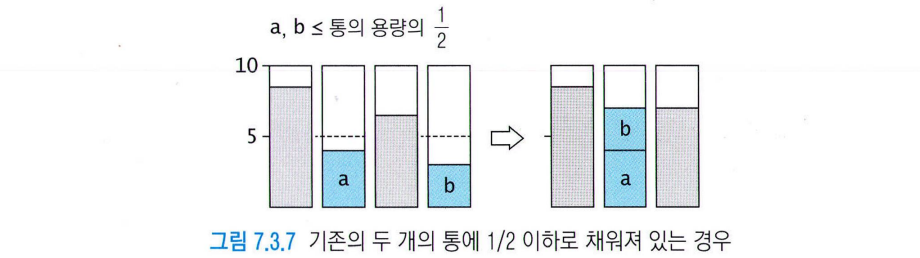
통의 용량 = C

• OPT : 최적해에서 사용된 통의 수
• OPT >= (모든 물건의 크기의 합) / C
• F = 각 방법이 사용한 통의 수
• F의 통 개수 중에서 많아도 1개 통이 1/2 이하로 차있고, 나머지 (F-1)개의 통은 반 이상 차있음 => 반이상이니까 C/2 곱해주자!

=> ((F-1) x C /2)와 모든 물건의 크기의 합 비교

(모든 물건의 크기 합) > (F-1) x C/2
➡️ (모든 물건의 크기 합)/C > (F-1)/2
➡️ OPT > (F-1)/2
➡️ 2OPT > F-1
➡️ 2OPT +1 > F
➡️ 2OPT >= F

결국, 근사비율 = 현재해/최적해 = 2OPT / OPT = 2.0

2) 다음 적합

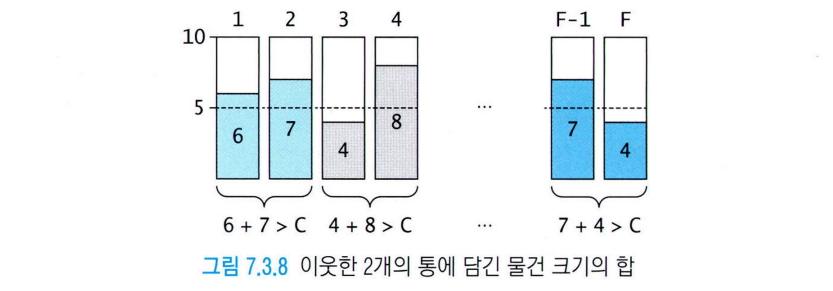
다음 적합으로 인해 물건을 담은 상태에서 사용된 통 중 반, F/2개의 통이 꽉 채워진 경우

(모든 물건의 크기 합) > (F/2) x C
➡️ (모든 물건의 크기 합)/C > F/2
➡️ OPT > F/2
➡️ 2OPT > F

결국, 근사비율 = 현재해/최적해 = 2OPT / OPT = 2.0