1. 관계 대수

1.2. 관계 대수

관계 대수 : 어떻게 데이터를 찾는지에 대한 질의를 수행할 것인가를 명시하는 절차적 언어

• 릴레이션에서 원하는 결과를 얻기 위해 연산을 사용해서 질의하는 방법을 기술하는 언어
• 절차적 언어 - 1개 이상의 릴레이션에 연산을 수행 -> 결과 릴레이션이 나오기까지의 절차를 표현함

1. 다음 용어들을 간단하게 설명하시오.
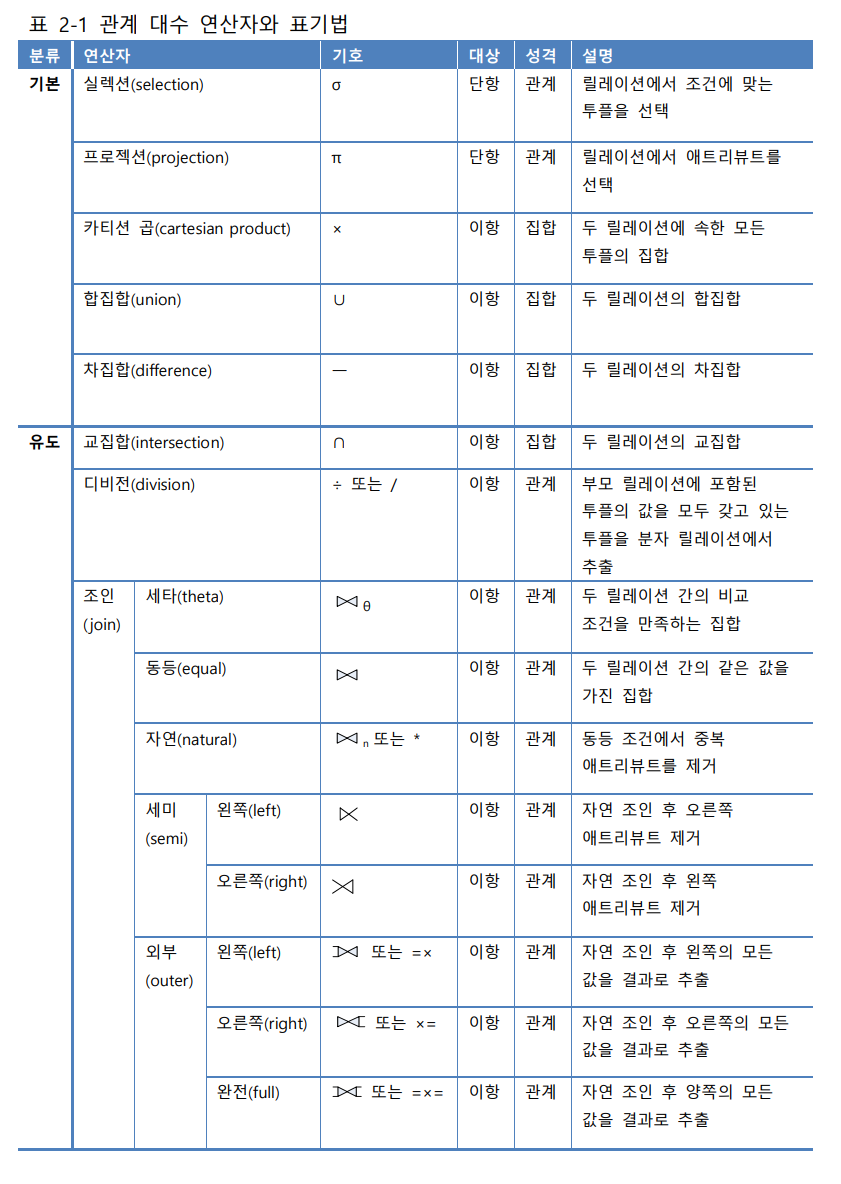
   (1) 관계 대수의 기본 연산자 : 합집합, 차집합, 카티션 곱, 프로젝션, 실렉션
   (2) 관계대수의 유도된 연산자 : 조인, 교집합, 디비젼
   (3) 관계 대수의 단항 연산자 : 실렉션, 프로젝션
   (4) 관계 대수의 집합 연산자 : 합집합, 교집합, 차집합, 카티션 곱
   (5) 합집합 호환 : 두 릴레이션의 애트리뷰트의 수가 같고, 대응되는 애트리뷰트들의 도메인이 같아야 함
   (6) 카티션 곱 : 두 릴레이션에 속한 모든 투플의 집합을 구함
   (7) 절차적 언어 : 데이터를 추출하는데 사용되는 연산 절차를 기술함. 어떻게 데이터를 찾는지 에 대한 질의를 수행할 것인가를 명시함
   (8) 세타 조인 : 두 릴레이션의 애트리뷰트 값을 비교하여 조건 세타를 만족시키는 투플만 반환
   (9) 동등조인 : 세타 조인에서 = 연산자를 사용한 조인
   (10) 자연 조인 : 조인에 참여한 애트리뷰트가 두 번 나오지 않도록 하나를 제거한 결과를 반환
   (11) 외부 조인 : 자연 조인 시 조인에 실패한 투플을 모두 보여주되 값이 없는 대응 애트리뷰트 에는 널값을 채워서 반환
   (12) 세미 조인 : 자연 조인의 결과 릴레이션에서 왼쪽, 또는 오른쪽 릴레이션만 반환

1) 집합 이론과 관계 대수 연산자

• 집합 이론이 집합 간 연산을 통해 결과 집합을 찾는 것 처럼
  관계 대수는 릴레이션 간 연산을 통해 결과 릴레이션을 찾는 절차를 기술함

단항 연산자 : 피연산자가 단일 릴레이션일 경우
이항 연산자 : 피연산자가 2개의 릴레이션일 경우
=> 연산자의 종류와 관계 없이 연산 결과는 항상 1개의 릴레이션임

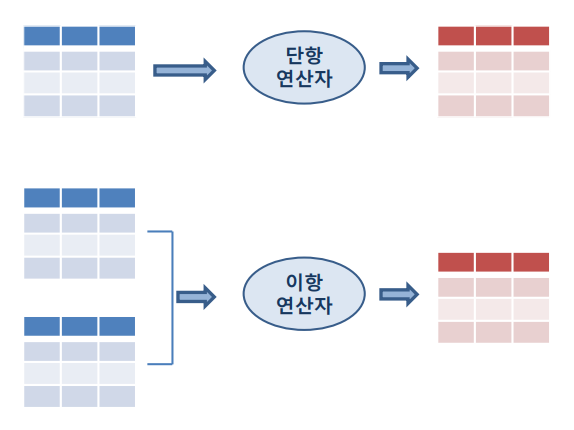
• 연산 결과로 반환되는 릴레이션엔 항상 중복된 투플들이 제외됨

2) 연산자의 구성

기본 연산자

• 합집합
• 차집합
• 카티션 곱
• 프로젝션
• 실렉션

유도된 연산자

: 기본 연산자들로부터 유도할 수 있는 연산자

• 조인
• 교집합
• 디비전

---

1.3 관계 대수 연산자

1) 셀렉션(selection) & 프로젝션(projection)

📌 셀렉션(= 실렉션) : 하나의 릴레이션에서 조건을 만족하는 투플들의 부분 집합을 추출하는 연산자

σ<실렉션 조건>(R)

• 1개의 릴레이션에 적용됨 -> 단항 연산자

• 결과 릴레이션의 차수(= 열의 수) = 입력 릴레이션의 차수

• 결과 릴레이션의 카디날리티(= 행의 수) <= 입력 릴레이션의 카디날리티
  => 당근인 말!🥕
  : select 한 결과를 생각해보면, 입력 릴레이션과 열의 수는 같음, 행의 수는 작거나 같기 때문
  

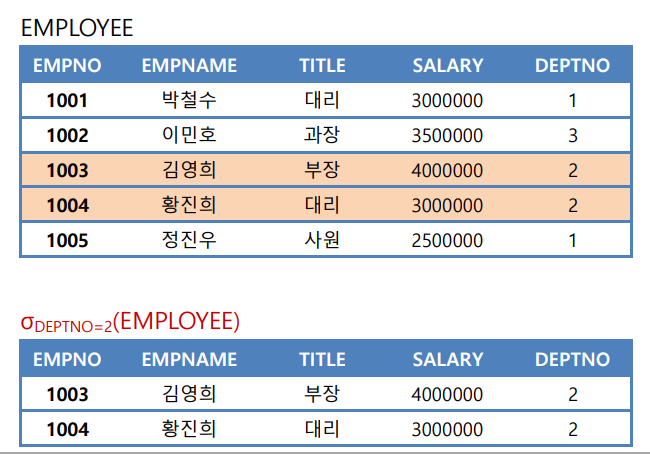
• [예제] 다음 EMPLOYEE 릴레이션에서 2 번 부서에 소속된 사원을 검색하시오.
  

📌 프로젝션(projection) : 하나의 릴레이션의 애트리뷰트들의 부분 집합을 구하는 연산자
π<애트리뷰트 리스트>(R)

• 1개의 릴레이션에 적용됨 -> 단항 연산자
  

• [예제] EMPLOYEE 릴레이션에서 사원들의 TITLE 과 SALARY 를 검색하시오
  

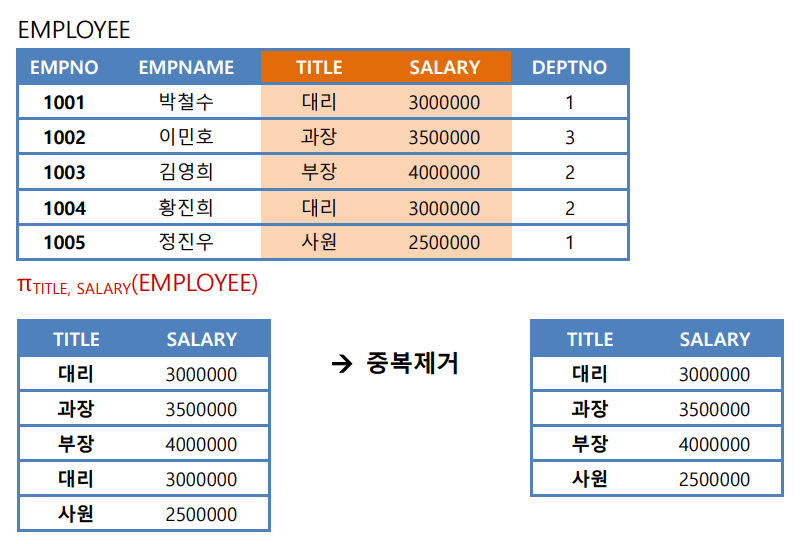
※ 관계 대수에서는 중복된 값이 있을 경우, 항상 중복이 제거된 상태가 된다. 후에 배울 SQL 질의에서는 중복 투플이 포함될 수도 있다. 만약 중복이 제거된 투플들을 얻기 원할 때는 다음과 같이 DISTINCT라는 키워드를 명시적으로 사용해야 한다.

SELECT DISTINCT title, salary
FROM EMPLOYEE

2) 집합 연산자

• 입력 릴레이션이 2개 -> 이항 연산자
  카티션 곱을 제외한 나머지(합,차,교집합) - 연산하려면 2개 릴레이션이 합집합 호환 / 형식 호환이어야 함

💡<2개 릴레이션이 합집합 호환이 되는 필요 충분 조건>
2개 릴레이션 R(A_1, A_2, ..., A_n) & S(B_1, B_2, ..., B_n)이 있을 때

• n = m
  => 두 릴레이션의 애트리뷰트의 수(= 차수)가 같아야 함
• 모든 1 <= i <= n 에 대해 domain(A_i) = domain(B_i)
  => 대응되는 애트리뷰트의 도메인이 같아야 함

📌 합집합 호환일 경우

• 2개의 릴레이션 R,S의 합집합, 차집합, 교집합의 결과 릴레이션 차수는 R&S의 차수와 같음
• 결과 릴레이션 애트리뷰트 이름 - 첫 번째 릴레이션 R의 애트리뷰트들 이름과 같음

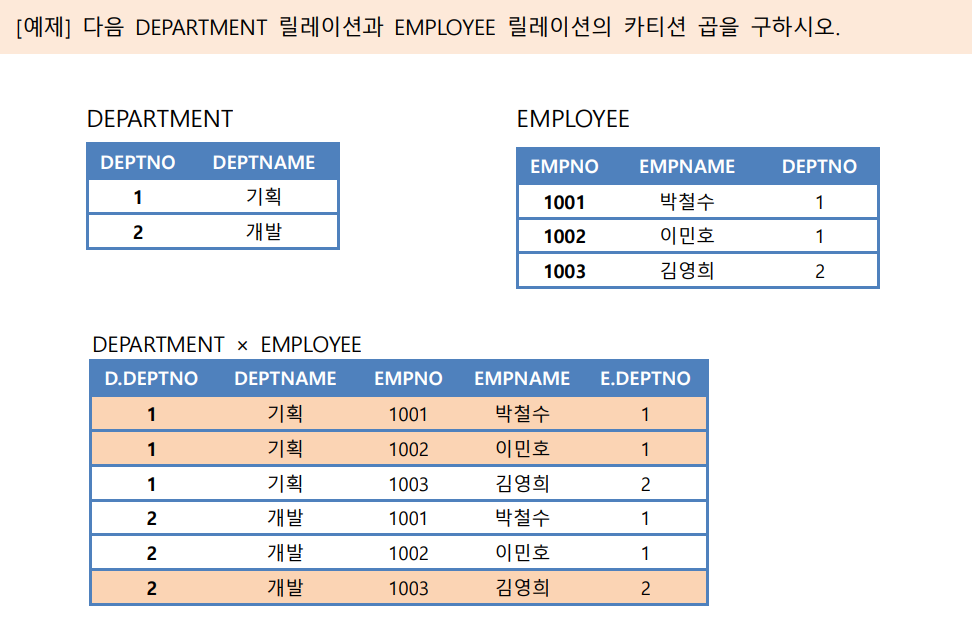
💡 [예제] 다음 DEPARTMENT 릴레이션과 EMPLOYEE 릴레이션은 합집합 호환을 만족하는가?

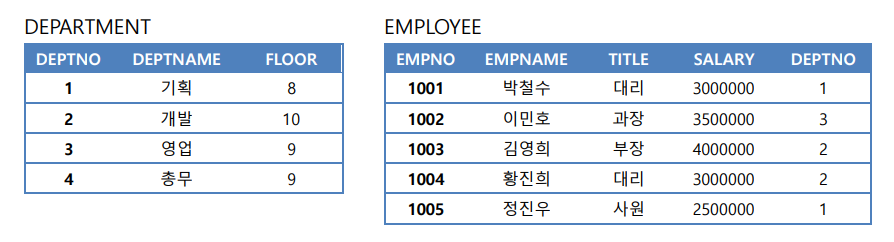
-> 여기선 DEPARTMENT에서 DEPTNO를 프로젝션한 결과 (πDEPTNO(DEPARTMENT)) & EMPLOYEE에서 DEPTNO를 프로젝션한 결과 릴레이션 (πDEPTNO(EMPLOYEE)
: 2개는 차수 같고, 도메인 동일 => 합집합 호환

💡 πDEPTNAME(DEPARTMENT)와 πEMPNAME(EMPLOYEE)은 합집합 호환일까?

-> 애트리뷰트 이름 다른 거 2개 (DEPTNAME, EMPNAME)의 도메인이 같은지는 인스턴스 값만 보곤 알 수 X
만약 둘다 CHAR(10)이면 합집합 호환

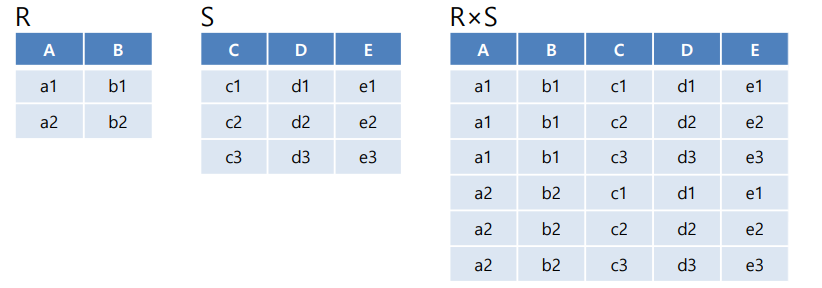
📌 카티션 곱 (= 크로스 곱)

💡 수학에서의 곱집합 (A X B)

• A 원소와 B 원소의 순서쌍의 집합
  A × B = { (x, y) | x ∈ A and y ∈ B}
• A={1, 2}, B={a, b, c}가 있을 때, A×B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}

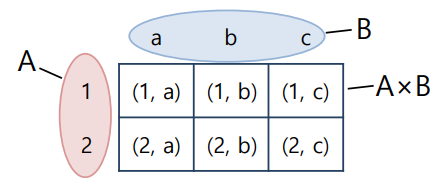
💡두 릴레이션의 카티션 곱 : 양쪽 릴레이션 투플들의 모든 가능한 조합으로 이루어진 릴레이션이 됨

R × S = { (x1, …, xn, y1, …, ym) | (x1, …, xn) ∈ R and (y1, …, ym) ∈ S}

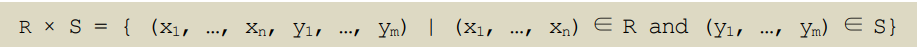
3) 조인 연산자

: 2개의 릴레이션으로부터 연관된 투플들을 결합하는 연산자

• 조인에 참여하는 애트리뷰트들이 서로 동일한 도메인이어야 함
• 합집합 호환일 필요는 X

<조인 연산 종류>

• 기본 조인 연산 : 세타 조인, 동등 조인, 자연 조인
• 확장된 조인 연산 : 외부 조인, 세미 조인

📌 세타 조인 & 동등 조인

• 세타 조인 : 두 릴레이션의 애트리뷰트 값을 비교 -> 조건 세타를 만족시키는 투플만 반환
  

-- 조인 조건 세타 : {=, <>, <=, <, >=, >} 중 하나
-- 세타 조인을 수행하기 위해서 양쪽 릴레이션에의 애트리뷰트들이 세타 조인을 만족하는
투플들만 골라낸다. 이것이 카티션 곱과 조인의 주요한 차이점

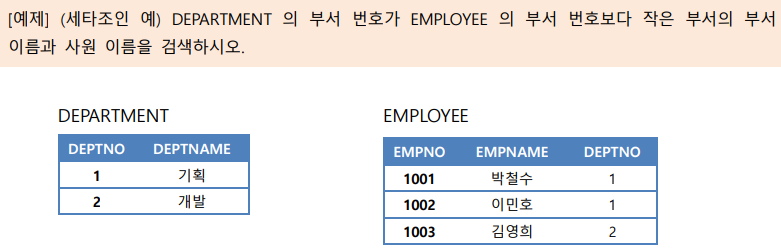
• 동등 조인(= 내부 조인(inner join)) : 세타 조인 중 비교 연산자가 '='인 조인
  

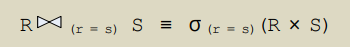
-- 양쪽 릴레이션의 애트리뷰트들의 값이 같은 투플(기본키 & 외래키 관계인 녀석들..)만 골라냄

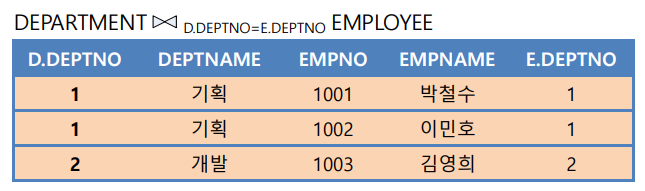
+) 두 릴레이션의 동등 조인 결과 = 카티션 곱에 selection 적용한 결과
*) 동등하다는 표현 (≡)

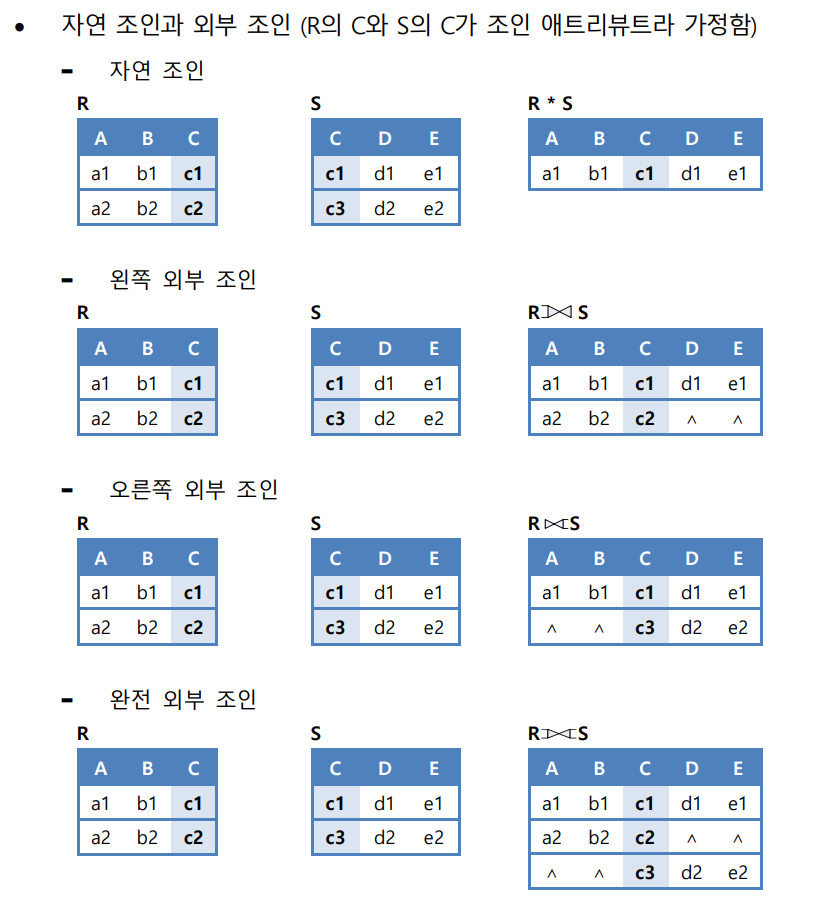
📌 자연 조인(natural join)

• 동등 조인의 결과에서 조인에 참여한 애트리뷰트를 1개 제외한 조인
  (조인할 때 겹치는 열은 1개로만 나온다는 말)
  

📌 외부 조인(outer join)

• 자연 조인을 한 뒤, 조인에 실패한 투플을 모두 보여줌
• 값이 없는 대응 애트리뷰트엔 null값을 채워서 반환
• 모든 투플을 보여주는 기준 릴레이션이 어느 쪽인지에 따라 왼쪽(left) / 오른쪽(right) / 완전(full) 외부 조인으로 나뉨

left outer join

right outer join

full outer join

📌 세미 조인 (semi join)

• 자연 조인의 결과에서 왼쪽 or 오른쪽 릴레이션만 반환하는 연산

(남아 있는 쪽이 삼각형 완성돼있음 하핫)

• left semi join : 자연 조인 후 오른쪽 릴레이션의 열들을 모두 제거

• right semi join : 자연 조인 후 왼쪽 릴레이션의 열들을 모두 제거

---

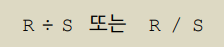
4) 디비전 연산자(division operator)

• 관계 대수의 다른 연산과는 달리 애트리뷰트 값의 집합으로 연산 수행
  

• R(Z) ÷ S(Y)가 P(X)를 반환하면
  : R(Z)의 차수가 m이고, S(X)의
  차수가 n이라면
  => P(Y)의 차수는 m - n
  => Z - Y = X이다.

R / S2는 {볼펜, 자}를 ‘모두’ 사용하는 학생들이 누구인지를 묻는 것과 같다. 이 학생들은
{10, 40}이다. R / S3는 {사인펜, 볼펜, 자}를 모두 사용하는 학생 = {10}번 학생임

5) 관계 대수 연산의 예

💡 [예제] 2 번 부서나 3 번 부서에 근무하는 모든 사원들의 이름과 급여를 검색하라.
projection(DNO = 2 OR DNO = 3)(selection(empname,salary)(EMPLOYEE))

💡 [예제] ‘개발’ 부서에 근무하는 모든 사원들의 이름을 검색하라.

6) 관계 대수의 한계

관계 대수의 한계점은 SQL에서는 모두 실행 가능함

(1) DB의 스키마 생성 & 수정 불가능
EMPLOYEE 릴레이션 생성 or 어떤 투플 삭제/추가 or 어떤 값을 수정(ex> SALARY의 10% 인상)해서 저장 불가능

(2) 산술 연산 불가능
ex) EMPLOYEE 릴레이션의 각 투플에 대해 SALARY 애트리뷰트 값이 10% 인상됐을 때 값을 알 수 없음

(3) 집계 함수를 지원 X

(4) 정렬 불가능
ex) 모든 투플들을 사원 이름 순으로 정렬하려고 표현 못함

(5) 중복된 투플을 표시 불가능

• SQL에선 기본적으로 중복된 투플 표현, 중복 없애려면 'DISTINCT' 키워드 사용