머신 러닝
Machine learning (ML)
여러가지 알고리즘
주로 정형 데이터를 다룬다.
그 중 인공신경망 -> Deep learning(DL) ( -> 생성형)
=> 주로 비정형 데이터들을 다룬다.
요즘은 ML + DL 추세 ~
알고리즘 종류
주로 Tree 기반.
- XGBoost
- Randomforest
- LightGBM
- CatBoost
...
머신러닝
2D Matrix 구조의 데이터.
(-> DL 3D Tensor 구조)
- Feature, 독립변수 X : 입력변수, 수집한 데이터 - 여러 개의 변수가 존재함
- Target, 종속변수 Y : 출력변수.
f(X)=w1X1+w2X2+..(w는 가중치)
Feature | Target
( Input) | (Output)
으로 나눌 수 있고,
Training Data (모델 학습에 사용)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
Testing Data (구축된 모델 평가에 사용)
로 나눈다
> 이 경우 절대 섞이면 안 됨!!! 성능이 잘 나오면 의심해봐야함..
+ 사이에 Validation Set (모의 검증) 을 사용하기도 한다. 약 5:3:2 비율

Parameter Estimation
Loss function
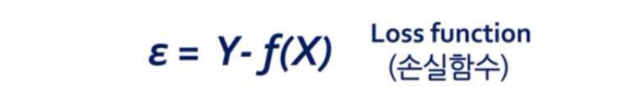
나의 이상향(실제 값)과 현실(모델 값)의 괴리 => 최소화 해야 함!
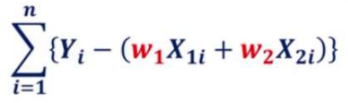
여러 Sample이 있는 경우 차이의 합 사용
Cost function
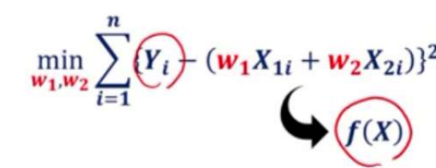
로 원래의 값(Y)과 가장 오차가 작은 가설함수(f(X)) 를 도출해야 함
** 제곱은 - 값을 고려한 것
f(X)
다중 선형 회귀 모델 / 로지스틱 회귀 모델 / DT / 인공 신경망

>> 이상과 현실이 동일하게. Target과 가깝게 fitting 해야함.
= function 값이 최소가 되는 최적의 parameter w0, w1, .. 찾기
Gradient Descent (GD)
경사 하강법으로 min 값 찾아서 parmeter 결정하기
x,y에 대한 값을 가졌을 때 f(X)에 대해 계수를 알아야 함.
예를 들어 선형이라고 가정하면, y=ax+b에서 a랑 b의 값을 최적으로 결정해야함.
1 . 먼저 하나의 변수 (a, 기울기)를 특정 상수라고 가정한 후 b를 구한다.
2-1. b를 구할 때도 먼저 특정 상수라고 가정한 후,
데이터 x로 y값을 계산하고 실제 y값과의 차잇값(= residual)을 구한다.
2-2. 모든 데이터들의 residuals의 제곱의 합(c, loss function)을 계산한다.
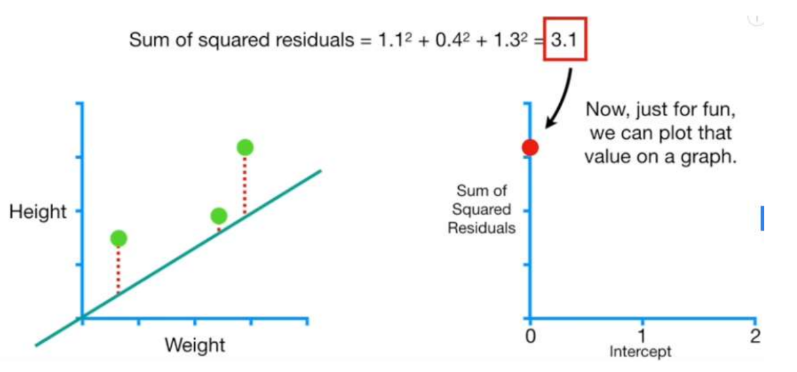
2-3. b 값을 다른 상수로 바꿔가면서 b와 c에 대한 그래프를 나타내본다.
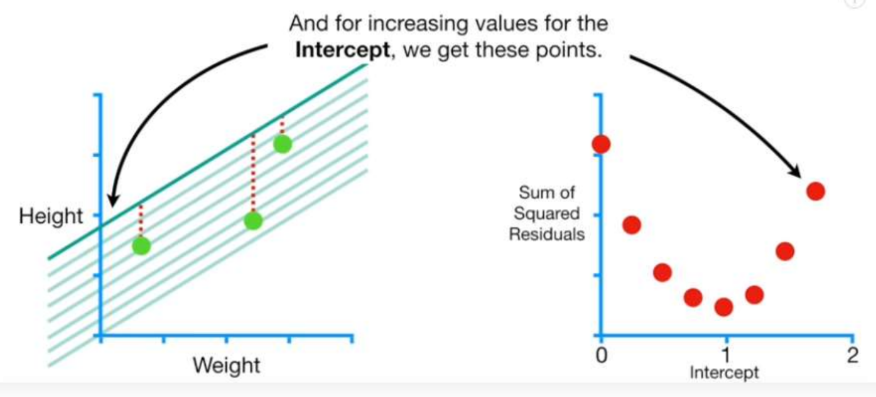
이 때 c의 최솟값( 최소의 residual합 )을 구하는 방법이 Gradient Descent!
2-4. residual 식을 써보면 {real Y - (ax+b)}^2 이다.
위 식을 미분하면 2{real Y - (ax+b)}이고 이 의미는 기울기이다.
* 이 때 우리는 지금 b를 구하고 있으므로 b에 대해 편미분한다.
2-5. 특정 b값에서 기울기 값을 계산한다.
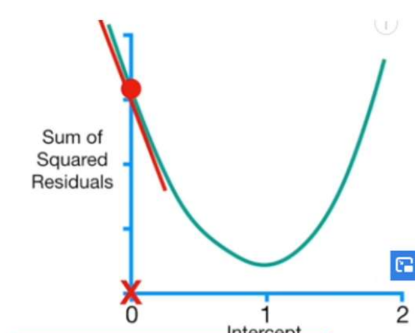
기울기가 음수이면 c가 감소하고 있다는 의미이기 때문에 더 큰 b값에서의 c를 찾아야 한다.
2-6. 다음 b값을 결정하는 방법은
계산한 기울기 값에 learning rate를 곱한 값을
원래 b값에서 빼준다. ( b는 기울기 부호와 반대되는 방향으로 변화해야함 )
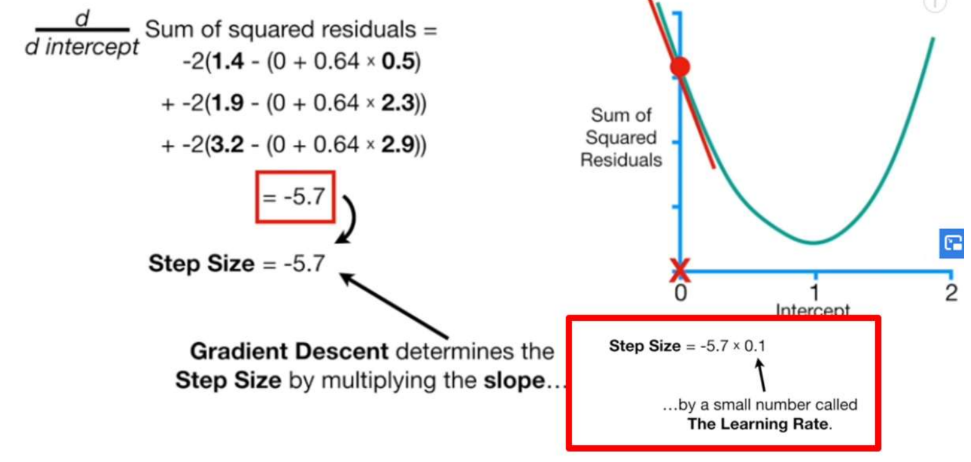

* learning rate는 본인이 설정한 값으로 얼마의 간격을 두고 보고 싶은지에 따라 결정한다.
* 기울기 값을 곱해주는 이유는 기울기 값(변화 폭)이 클 경우 더 넓은 간격을 두고 찾기 위해서이다.
2-7. 새로운 b값에서 위 2의 과정을 반복하여 또 새로운 b값을 찾고,
계속 반복하다 Step Size 가 충분히 작아졌을 때에 최종 b값( 최솟값 c )으로 결정한다.
3 . 우리가 찾아야 할 파라미터는 2개(a,b) 이므로
두 파라미터를 모두 변동하면서 최솟값을 찾는 3D의 측면에서
Gradient Descent을 진행해 파라미터 값을 찾는다.
-> 편미분느낌~
모델 평가
회귀 VS 분류
-
회귀 / MSE, RMSE ..etc
실제 숫자를 예측하는 모델- Means Square Error(MSE) :
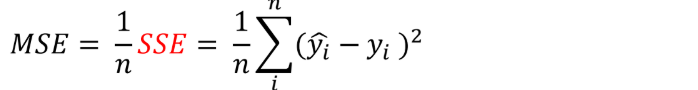
- Coefficient of Determination, R-Squared :
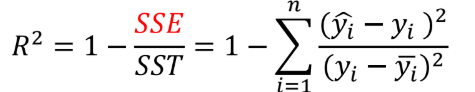
- Means Square Error(MSE) :
-
분류 / Confusion Matrix
어떤 클래스에 속할지 예측 or 특정 클래스에 속할 확률 추정- 이진 분류 : 양성/음성 클래스.
- 다중 클래스 분류 : 모델의 전체적인 성능 + 각 클래스 별 성능 비교
- 다중 레이블 분류 : 앞 두개는 결과가 상호보완, 이 경우 배타적 X 혼재 O
이진 분류의 Confusion Matrix
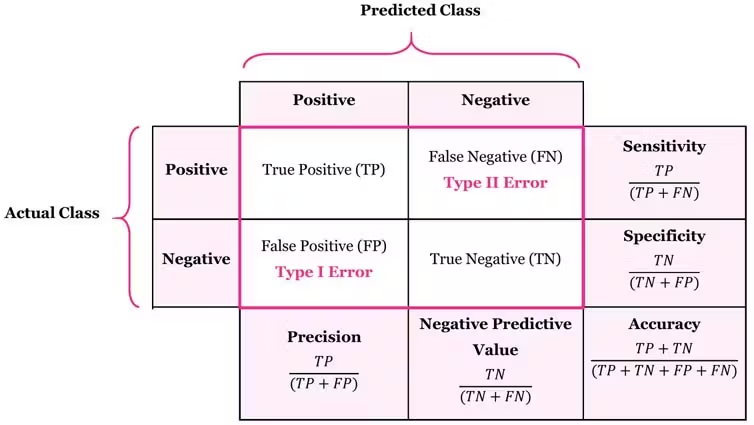
>> TP와 TN이 모델이 예측 성공한 것! >> 반대로 FP와 FN은 모델의 에러
모델 평가지표
Accuracy = (TP+TN) / Total : 전체 데이터 중 예측 성공률
Precision = TP / (TP+FP) : 모델이 해당 데이터라고 예측한 것들 중 예측 성공률
Recall = TP / (TP+FN) : 실제 해당 데이터들 중 예측 성공률
만약 실제 데이터가 1%의 확률로 1(Positive)이라면,
FN은 거의 없을 것임 == precision 이 중요하겠지?
ex. 메일 스팸 분류기 ( 스팸(1) vs 정상(0) )
스팸 메일인데 정상 분류 = FN error
ㄴ 그냥 클릭 한 번 더 함,.. 메일함에 스팸메일 하나 쌓임..
정상 메일인데 스팸 분류 = FP error
ㄴ 중요 메일의 경우 경제적 손해 발생... 고소 들어감..
=> 둘 중에 하나를 선택해 줄여야 한다면 FP ERROR !!
==> 모델 평가 지표를 Precision으로 !!! TP
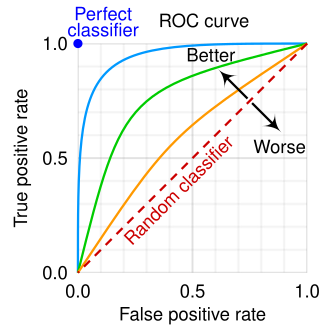
ROC curve
Bias-Variance Tradeoff
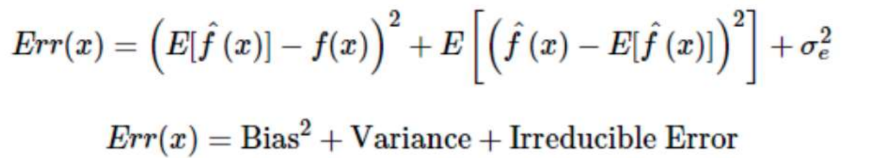
Bias(편향, 실제 값과 예측 값의 차이)
Variance(분산, 예측 값들의 관계. 예측 평균과 얼마나 떨어져있는지)
두 가지 오차를 최소화 해야함!
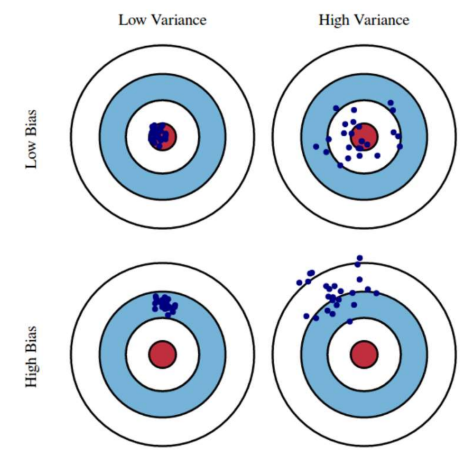
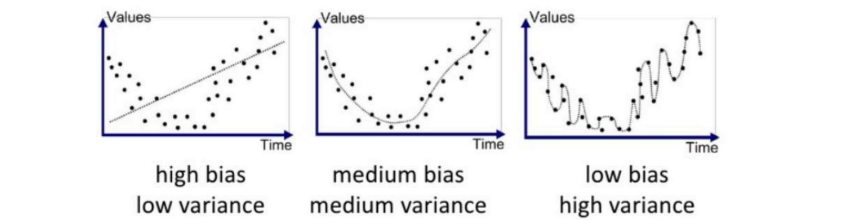
모델이 simple해지면 variance↓, bias↑ (sample마다 fit이 잘 안됨. underfit)
모델이 complex하면 variance↑, bias↓ (입력값이 조금 달라져도 변동폭이 너무 클 수 있음. overfit).
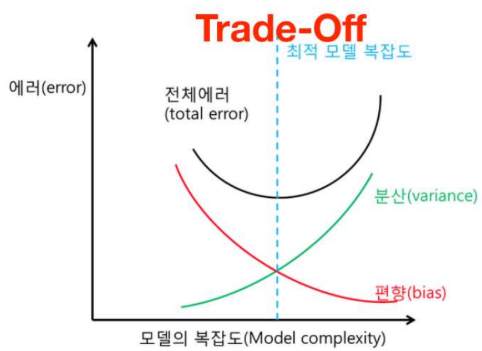
둘 다 완벽히 줄일 수는 없으니 적당한 Bias, variance의 최적값을 찾아야 함. 주관적인 판단
❗ 모델링의 목적은 에러를 최소화 하는 것이 아님.
새로운 Sample에서도 general한 결괏값을 얻는 것임!!