문제 해석
- 문제 자체는 이해하는데 어려움이 없는 문제이다.
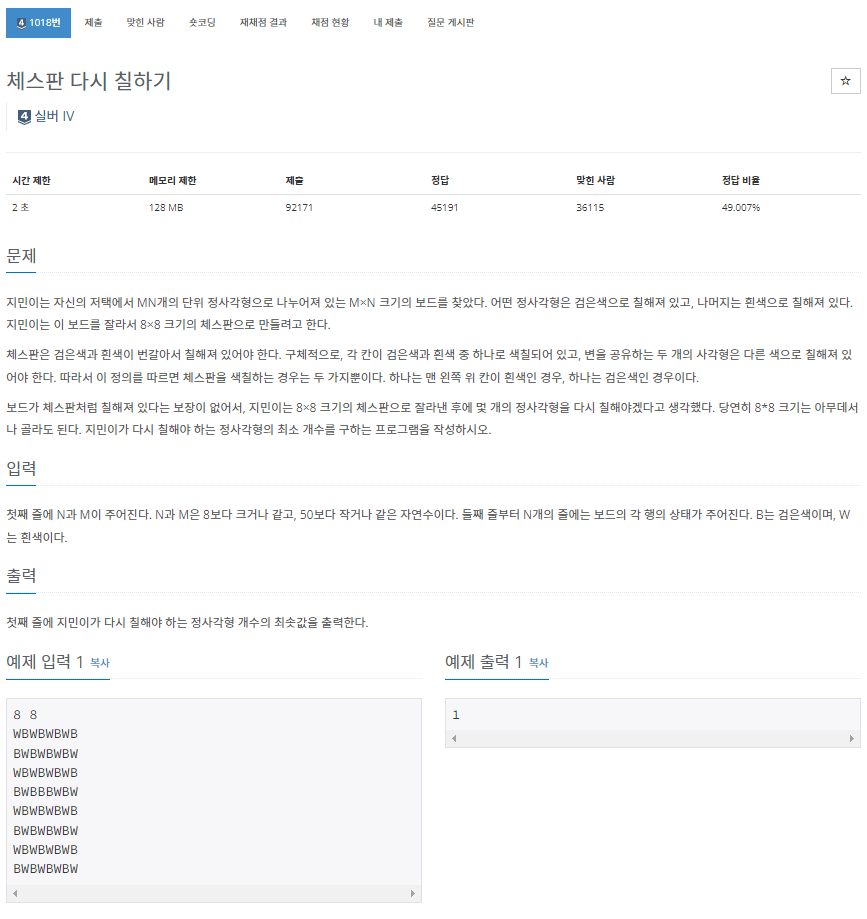
- 일단 체스판의 크기를 입력받고, 그 크기만큼 체스판의 색을 입력받는다.
- 체스판을 보면 위와 같이 검정(B)와 흰(W)로 칸이 번갈아가며, 체스판을 색칠한다.
- 또한, 입력받은 체스판의 크기가 8X8이 아니면,8x8로 잘라줘야한다.
- 바꾸는 값의 횟수가 가장 적은 체스판으로 자르고, 그 최소비용을 출력하면 되는 문제이다.
- 즉, 체스판을 조건은
- 같은 라인의 줄에서 색을 번갈아가며 색칠한다.
- 라인을 넘어갈때(다음 줄)일때는 바로 직전의 색(넘어가기전의 줄의 마지막 색)으로 시작한다.
- 간단하게 위의 조건만을 가지고 문제를 풀려고 했는데, 간단하게 위의 조건만으로 풀려고하면 풀리지 않는다.
-
위의 사진과 같이 시작 색이 다를 수 있기 때문에, 그 경우도 잘 생각해서 알고리즘을 짜야한다.. (벌써 어려움...😂)
-
풀리지가 않아서 체스판 다시 칠하기영상을 보고 이해했다...
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int getMinCost(int startrow, int startcol, String[] chessboard) {
String[] board = {"WBWBWBWB", "BWBWBWBW"}; // 화이트 버전, 블랙버전
int whiteVerCount = 0; // 화이트를 기준으로 최소 비용을 고를 예정
for(int i = 0; i < 8; i++){ // 세로 8
int row = startrow + i; // 매개변수로 받은 chessboard의 값의 인덱스는 8X8이 아닌 전체 범위이기때문
for(int j = 0; j < 8; j++){ // 가로 8
int col = startcol + j;
if(chessboard[row].charAt(col) != board[row%2].charAt(j)){
whiteVerCount++;
}
}
}
// whiteVerCount는 하얀버전으로 체스판을 자를때의 최소비용이고 64 - whiteVerCount하면 블랙의 최소비용이다.
// 왜냐면, 체스판의 최대 크기가 8x8이기 때문
return Math.min(whiteVerCount, 64-whiteVerCount);
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); //세로줄 크기
int M = Integer.parseInt(st.nextToken()); // 가로줄 크기
String[] chessboard = new String[N];
for(int i = 0; i < N; i++){
chessboard[i] = br.readLine(); //한줄씩 입력받는 String형 배열
}
br.close();
int count = Integer.MAX_VALUE; //가장 큰값으로 지정해두고(초기값)
for(int i = 0; i <= N-8; i++){
for(int j = 0; j <= M-8; j++){
int resultCount = getMinCost(i, j, chessboard);
if(count > resultCount){
count = resultCount;
}
}
}
bw.write(count + "\n");
bw.flush();
bw.close();
}
}코드 풀이
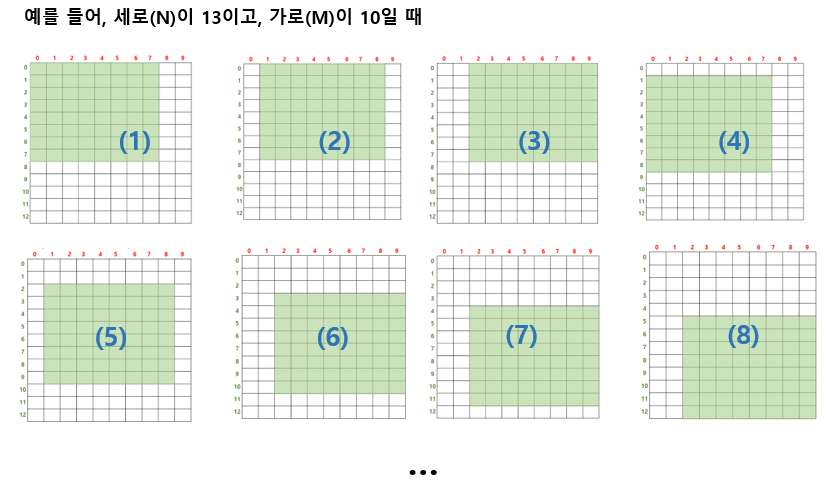
- 이런식으로 잘라서, 최소로 칠할 수 있는 범위의 체스판을 고르면 된다.
int count = Integer.MAX_VALUE;
for(int i = 0; i <= N-8; i++){ //8X8크기로 지정하기 위해 N-8만큼 반복
for(int j = 0; j <= M-8; j++){//8X8크기로 지정하기 위해 M-8만큼 반복
int resultCount = getMinCost(i, j, chessboard);
if(count > resultCount){
count = resultCount;
}
}
}-
여기서 M-8을 한 이유는 (1) ~ (3)을 보면 차피 8x8이기 때문에 딱 M-8만큼 한 값 만큼만 반복하면 가로 끝까지 닿는다.
-
마찬가지로 N-8을 한 이유는 (3) ~ (8)을 보면 아래로 한칸씩 내려오는 것을 볼 수 있는데(가로는 움직임은 신경X) 보면 N-8만큼만 하면 세로 끝까지 닿는 것을 알 수 있다.
-
그래서 반복문도 가로 세로 각각 -8씩 해주었다.
-
그 다음에는 핵심 로직인데, 바로 최소 움직임(비용)을 찾는 로직 getMinCost()메소드이다.
-
인수로는 세로의 시작점, 가로의 시작점, 전체 입력받은 체스보드배열이 있다.
-
세로의 시작점과 가로의 시작점은 위에서 말했듯이, -8만큼 각각해줬기 때문에 그것을 기준으로 배열 탐색을 시작한다.
-
일단 흰색 버전은 WBWBWBWB이고, 블랙 버전은 BWBWBWBW라고 가정하자.
String[] board = {"WBWBWBWB", "BWBWBWBW"};- 체스 보드의 크기는 고정으로 8X8임으로, 세로는 8번 반복하고, 세로를 기준으로 가로 8x8반복해야한다.
for(int i = 0; i < 8; i++){ // 세로 8
int row = startrow + i; // 매개변수로 받은 startrow(세로의 시작점)
for(int j = 0; j < 8; j++){ // 가로 8
int col = startcol + j; // 매개변수로 받은 startcol(가로의 시작점)
if(chessboard[row].charAt(col) != board[row%2].charAt(j)){
whiteVerCount++;
}
}
}-
가로와 세로는 매개변수로 시작점을 받았기 때문에 그를 기준으로 인덱스를 늘려 탐색해야한다!아니면 배열에 모순이 생겨버림 => 그래서 만든 것이 row, col 변수이다.
-
그리고 나서 인수로 받은 전체 배열(NxM)의 해당 row의 col값과 board[row%2]
- board[row%2] : board는 위에서 정의한 "WBWBWBWB", "BWBWBWBW"의 값이 있고 배열의 요소는 딱 2개이기 때문에 row%2를 하여 나머지로 반복하며 값을 전달해야한다.
- 흰색 버전을 기준으로 시작하는데 "WBWBWBWB"를 이전 줄에서 했다면 다음 줄은 "BWBWBWBW"이어야함. => 즉 row%2를 하면 값이 번갈아가면서 할당됨.
-
아무튼, board 배열의 row%2 인덱스의 요소의 j번째 문자가 다를 경우는 다시 칠해야하는 경우 이므로(패턴이 안맞다는 뜻!) 따로 뺐던 whiteVerCount(다시 칠해야하는 횟수를 저장하는 변수)를 증가시킨다.
-
블랙버전, 화이트버전 각각 탐색하여 값을 구해줘도 되지만, 최적의 효율인 코드를 짜기 위해 기준을 잡고 최소비용을 고르는 방법 설명한다.
-
어차피 체스 보드의 크기는 8x8이다. 그렇기 때문에 8x8(=다 바꾸는 경우가 8x8) - 하얀버전으로 시작한 다시 칠해야하는 횟수을 해주면 블랙버전일 경우의 바꿔야하는 횟수이다.
-
그 두개의 값을 비교해서 최솟값을 찾으면 최소 비용(횟수)의 값이 나온다.
return Math.min(whiteVerCount, 64-whiteVerCount);결과
느낀점
- 이번 문제 어렵게 느껴져서 결국 또 참고하여 이해하고 풀었지만... 내 스스로 정리하니까 이 문제를 좀 완벽하게 이해할 수 있었던 것 같다.
- 요 근래는 다른 분의 코드를 안보면 거의 풀 수 없는 것 같은 느낌인데, 앞으로는 1일 1포스트를 못하더라도 혼자 쭉 풀어볼 시간을 많이 가져야겠다는 생각을 많이 했다..(생각하는 끈기가 너무 없음...😦)
