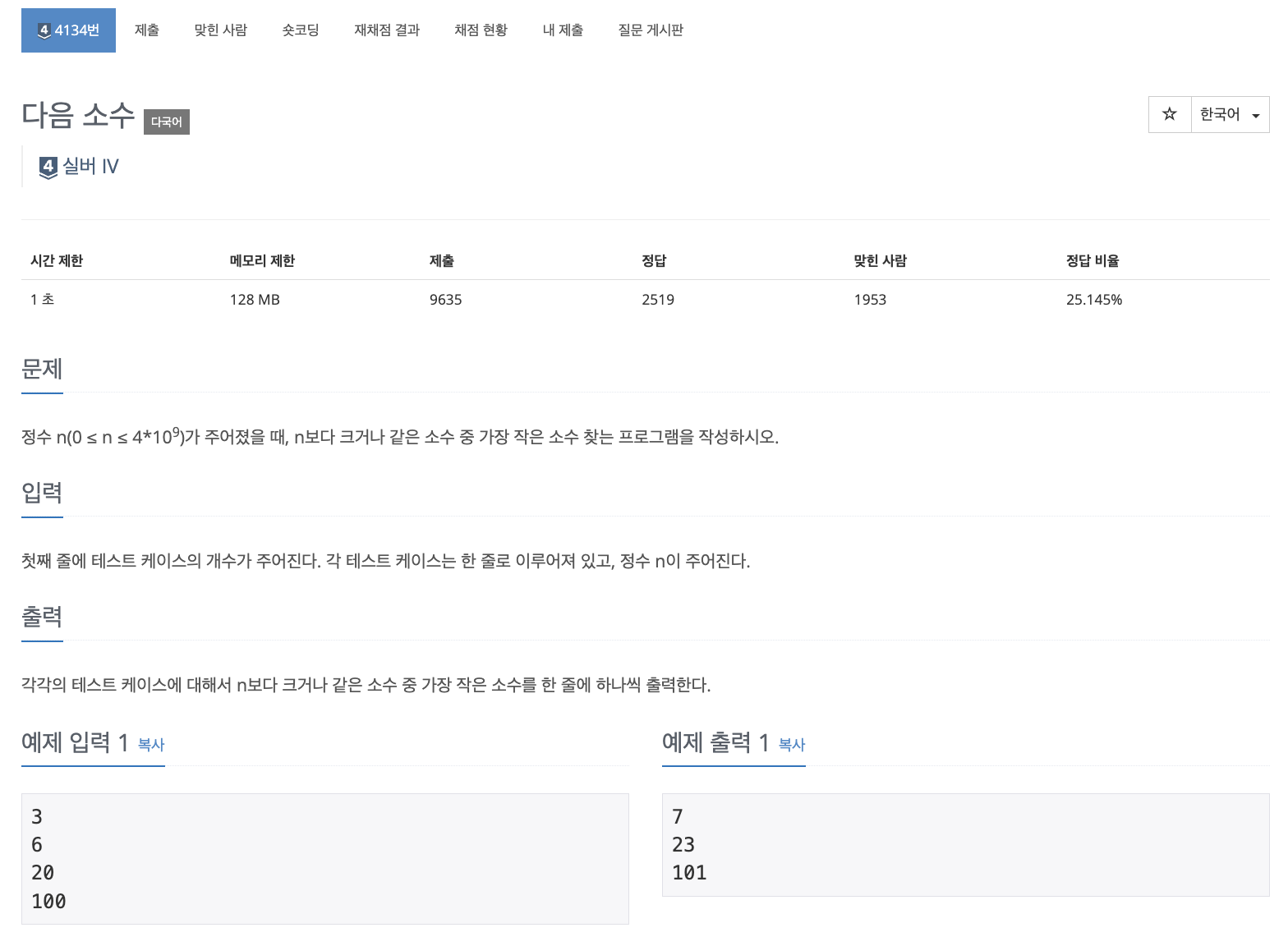
문제 해석
- 문제는 간단하다. 일단 입력받을 정수의 개수(테스트 수 ; T)을 입력받아 정수를T개 만큼 입력받는다.
- 입력을 모두 받았다면 입력받은 각각의 정수를 가지고 입력받은 정수보다 같거나 크면서 가장 작은 소수를 찾으면 되는 문제이다.
코드
import java.io.*;
import java.math.BigInteger;
public class Main {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
long[] numbers = new long[T];
for(int i = 0; i < T; i++){
numbers[i] = Long.parseLong(br.readLine());
}
br.close();
printSection(numbers);
}
static BigInteger findPrimeNumber(BigInteger num){
if(num.isProbablePrime(10)){
return num;
}else{
return num.nextProbablePrime();
}
}
static void printSection(long[] array) throws IOException {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
for(int i = 0; i < array.length; i++){
BigInteger bigNumber = new BigInteger(String.valueOf(array[i]));
bw.write(findPrimeNumber(bigNumber) + "\n");
}
bw.flush();
bw.close();
}
}
설명✏️

- int형과 long형의 범위는 위의 표와 같다.
- 만약 int와 long의 범위를 넘어가게 되면 0으로 출력되거나 에러가 발생할 수있다.
- 이를 해결하기 위해 나온 것이 BigInteger이다.
- BigInteger은 문자열 형태로 이루어져 있어 숫자의 범위가 무한하기에 어떠한 숫자이든지 담을 수 있기 때문에 무한의 정수가 들어갈 수 있는 가능성이 있다면 BigInteger이라는 클래스를 활용하는 것이 좋다.
BigInteger bigNumber = new BigInteger("숫자형태의 문자열");
BigInteger bigNumber = new BigInteger(String.valueOf(array[i]));
BigInteger 제공
- BigInteger에는 다음과 같은 메소드를 제공한다.
- isProbablePrime(10) : 현재 값이 소수인지 아닌지 판단하는 메소드
- isProbablePrime()메소드에 인자로는 certainty에 대한 값을 넘겨야 하는데 대략 10의 값을 넘기면 해당 값이 소수인지에 대한 판별률이 99.9%에 가까워지기 때문에 10을 매개변수로 넘긴다.
- nextProbablePrime() : 다음 소수 값을 반환해주는 메소드
- BigInteger보다 큰 첫 번째 정수를 보유하는 Biginteger를 반환
결과

느낀 점
- 이번 문제에서 처음 본 BigInteger에서 제공하는 메소드인 isProbablePrime()와 nextProbablePrime()을 처음알게 되었는데.. 처음에는 for(int i = 1; i <= 입력받은 숫자; i++) 해서 하나씩 비교하려고 했다.
- 하지만, 위와 같이 하나씩 비교해서 나눠지는 값의 횟수가 2초과(자신과 1은 차피 나누어질 테니까)할 시 입력받은 숫자+1을 해서 다시 for(int i = 1; i <= 입력받은 숫자+1; i++)해서 구할려고 하니까 시간 초과가 날 것 같았다. (맞는 방법인지도 모르겠고)
- 일단 제한 시간이 1초인데 위와 같은 방식은 반복문이 중첩되어 O(n²) 시간복잡도를 가지게 된다.
- 또한 입력 값이 int형도 long형도 아닌 bigInteger이라서 (물론 입력값 자체는 4x10⁹ 이지만 이보다 같거나 큰 소수를 찾아야하기 때문에 더 커야한다.)
- 암튼 이러한 큰 숫자를 for문을 중첩하여 구할려고 하면 시간을 많이 잡아먹을 것이 뻔했다.
- 그래서 자바에서 지원하는 소수를 구해주는 API가 있을까 찾다가 isProbablePrime()와 nextProbablePrime()을 찾게 되어 그대로 사용하게 되었다.



