그리디 알고리즘(Greedy Algorithm)이란?
- 말 그대로 Greedy(=탐욕) 알고리즘으로, 현재 시점에서 가장 좋은 선택을 하는 알고리즘이다.
- 다시 말해서, 현 시점에서 선택한 것이 나중에 어떠한 결과를 초래하는지 고려하지 않는다고 말할 수 있다.
- 그러한 특징으로 이 알고리즘은 항상 최적해를 보장하지 않는다.
- 그림으로 예시를 들어보면 아래와 같다.
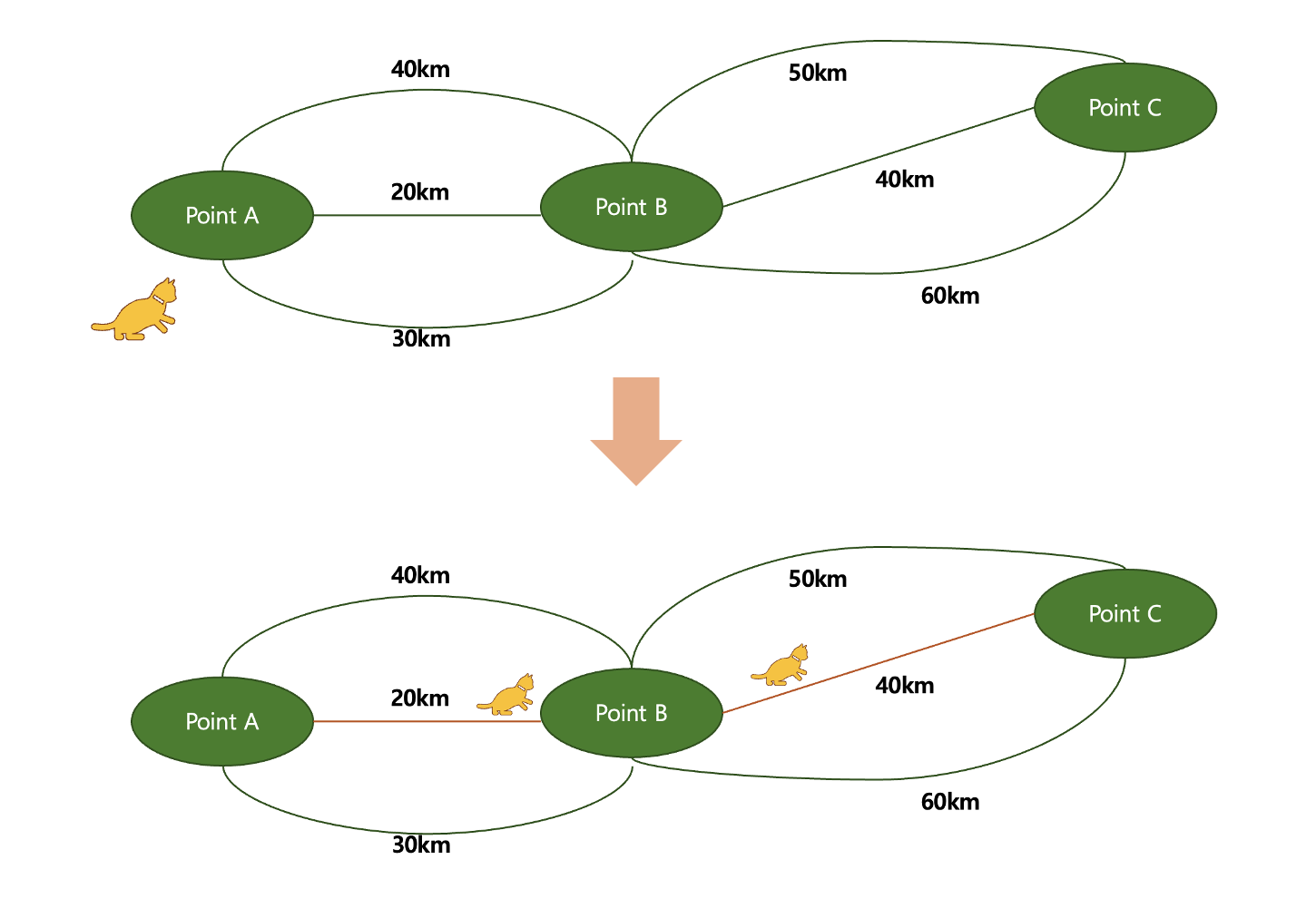
- 위와 같은 길이 있다면, 가장 최적의 길은 당연히 20km + 40km 일 것 이다.
- 하지만, 길이 아래와 같이 하나가 더 생긴다면??
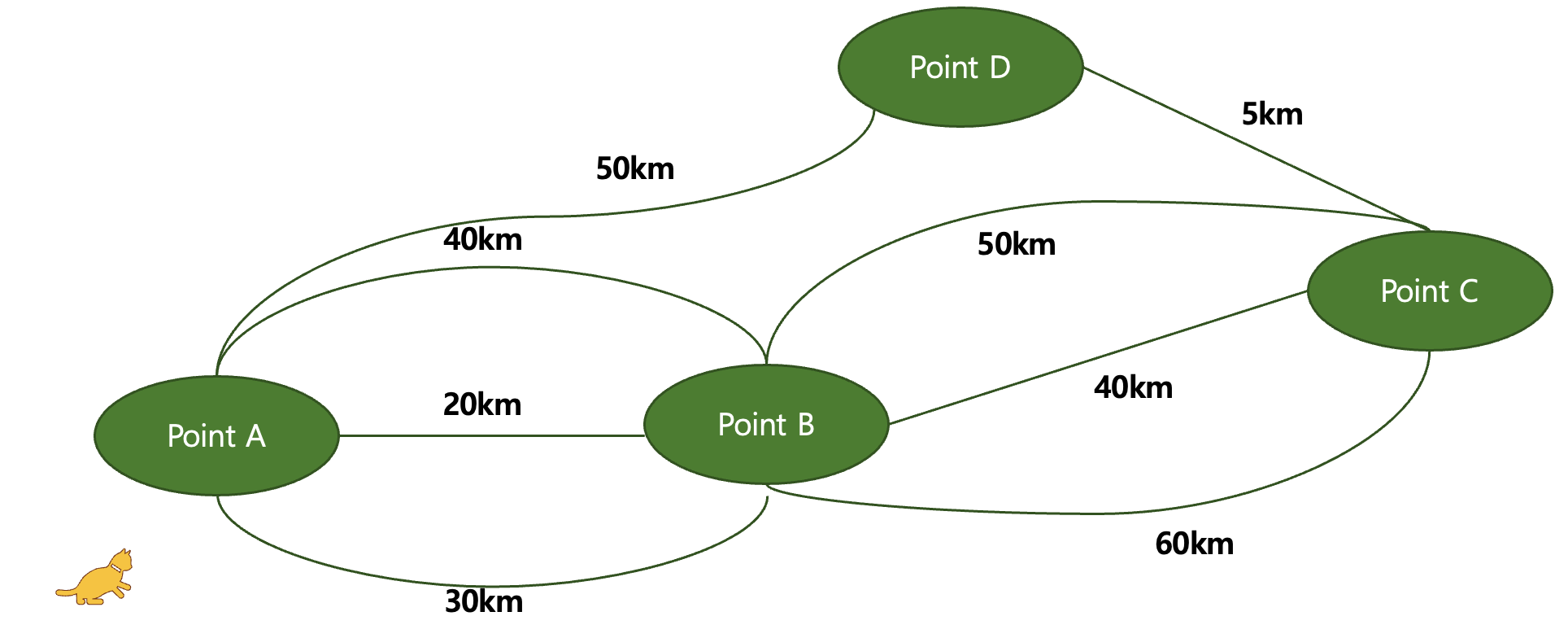
-
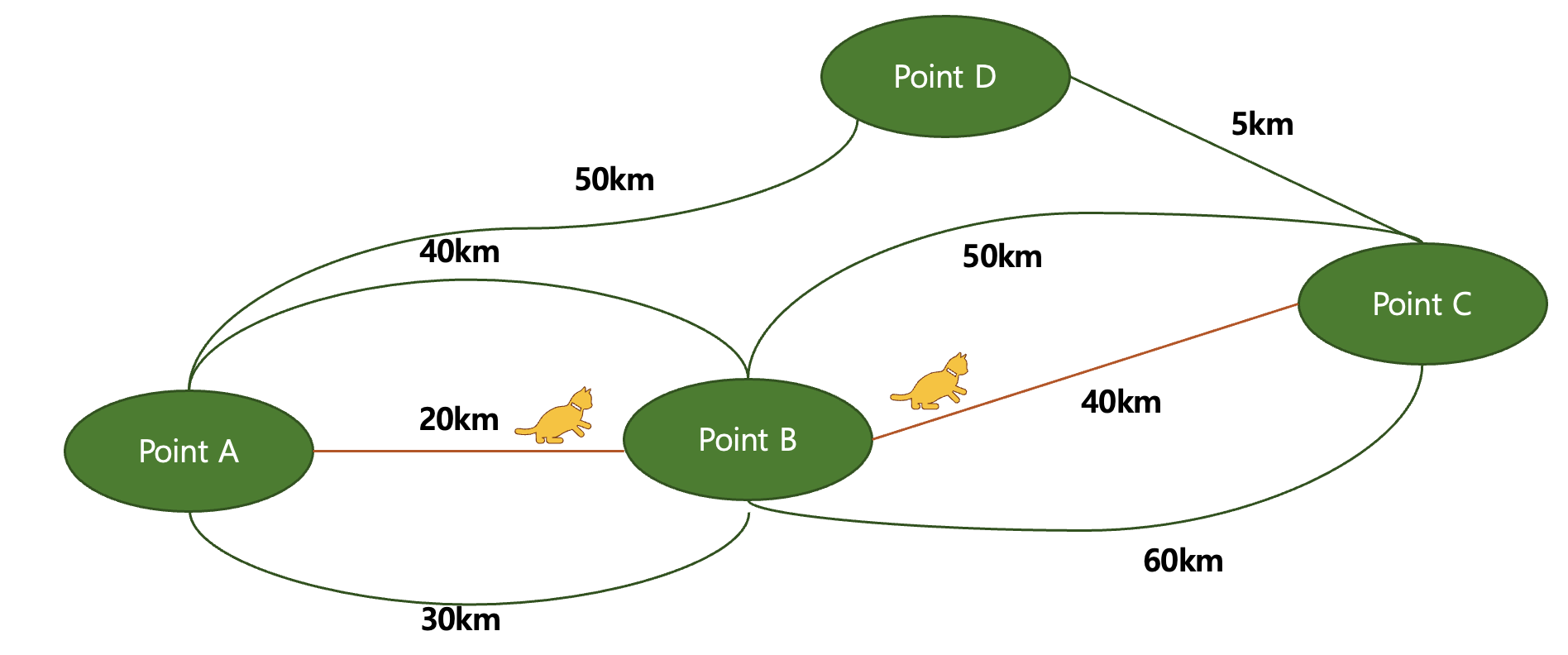
그리디 알고리즘으로 따지면 "😺"는 20km + 40km의 길을 또 한번 더 걸을 것이다. (왜냐면 그게 각 단계의 최선의 값이니까...)
-
하지만 보다시피 최적의 거리는 50km + 5km = 55km이 되어야 한다. (최단 거리)
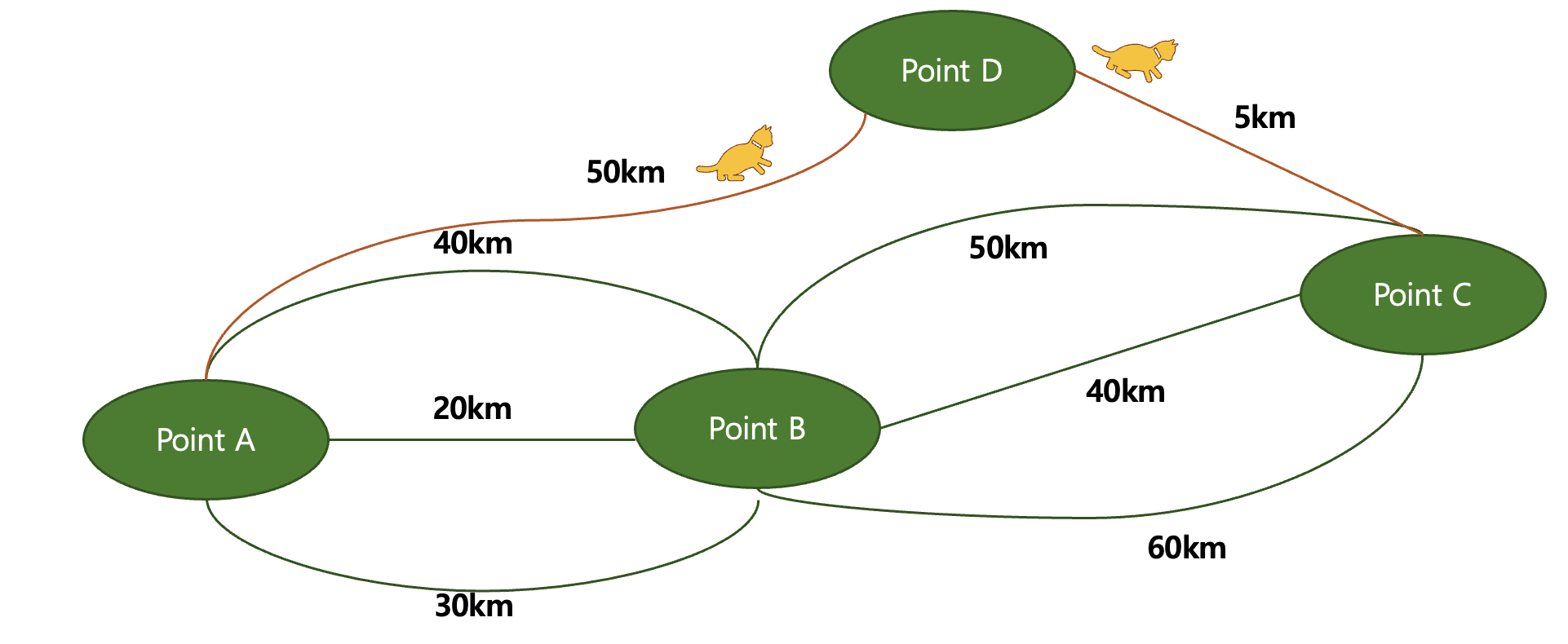
-
이렇게 그리디 알고리즘은 최적의 해를 항상 보장하지 못하는 데 최적의 해와 근사한 값을 구한다하여 이를 근사 알고리즘이라 볼 수 있다.
근사 알고리즘(Approximation Algorithm)이란?
- 최적의 해를 구할 수 없는 문제에서 근사한 해를 구하는 알고리즘으로 근사 알고리즘은 항상 최적해를 보장하지는 않지만, 많은 경우에는 최적해에 근접한 값을 구할 수 있는 특징을 가지고 있다.
- 그렇기 때문에 단기적인 목표를 중심으로 문제 해결에 초점을 맞추고 있다.
그리디 알고리즘(Greedy Algorithm)의 속성
탐욕 선택 속성(Greedy Choice Property)
- 각각의 ‘최선의 선택’들이 모여 전체 문제에 대한 최적해가 되어야 한다는 의미. 즉 위에서 본 예시처럼 각각의 최선의 선택이 전체의 최적해가 되지 않았을 경우 그리디 알고리즘은 최적해를 구하지 못하기 때문에, 각 단계의 선택들이 전체 문제에 대한 최적해를 도출할 수 있어야 한다.
최적 부분 구조(Optimal Substructure)
- 전체 큰 문제를 작은 부분 문제로 나누고, 각각의 부분 문제의 최적해를 조합하여 전체 문제에 대한 최적해를 도출할 수 있어야 한다.
예시 문제
- 대표적인 문제로 전 포스트 였던 POST-11047- 동전 0 문제가 있다. (문제 풀이는 해당 포스트에 올려놓았으므로 생략...)
느낀 점
그리디 알고리즘이 개념적으로는 크게 어려운 점이 없는 것 같다. (아니면, 깊게 보지 않아서 그런 거일수도 있고...) 아무튼 글로 설명하기에 부족함 감이 있는 것 같지만, 백준 그리디 알고리즘 문제를 풀어가면서 적용시켜 익히는 방향으로 진행하고자 한다!
