기타
1.DOM 구조

Document Object Model(문서 객체 모델)의 약자로 W3C(www, 월드 와이드 웹 컨소시엄으로 웹 기술의 표준을 정의하는 공식 기관)의 표준 객체 모델이며 HTML요소를 Javascript Object처럼 조작할 수 있는 Model이다. 다시 말해, X
2.Socket(소켓)

네트워크를 경유하는 프로세스 간 통신의 종착점(응용계층)은 데이터 송수신을 위해 반드시 소켓을 거쳐 전송 계층으로 데이터를 전달해야 한다.Client와 Server는 자신의 IP 주소와 소켓 연결에 할당할 Port 번호를 End Point로 삼고, IP주소와 Port
3.CORS
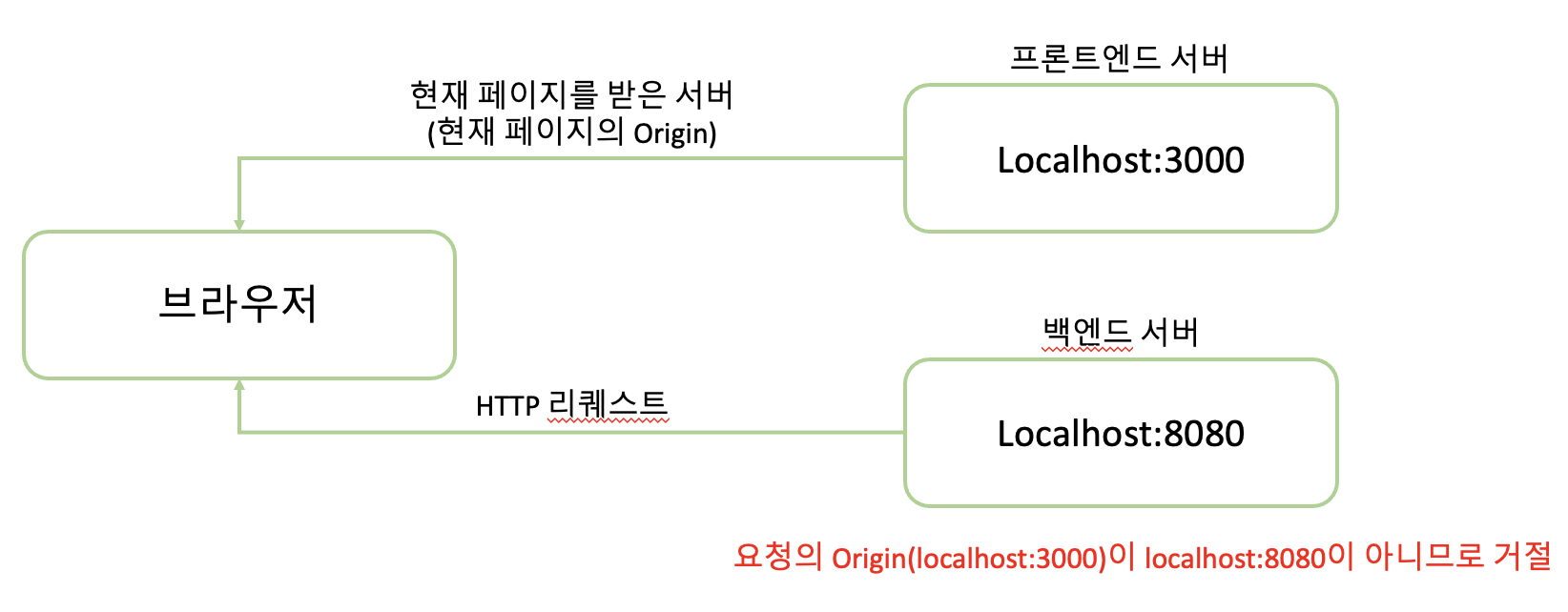
" 웹 개발을 하다보면 CORS 정책 위반으로 인해 에러가 맞닥뜨리는 상황은 굉장히 흔해서 누구나 한 번 정도는 겪게 된다고 해도 과언이 아니다." 이미지 출처 > #### 도대체, 이 에러는 무엇이길래 발생하는 걸까? 이 POST는 이 CORS에 대해 설명하고자
4.웹 프로젝트

1. 웹 프로젝트의 기본 구조(JAVA) JAVA를 이용해서 웹을 개발하는 경우 기존의 자바 개발 환경과 다르다. 즉, 개발자가 코드를 정해진 구조에 넣는 방식으로 개발을 진행해야 한다. 대부분의 웹 프로젝트들은 아래와 같이 같은 네트워크(서버)를 통해서 연결되는 구조
5.Web MVC 방식
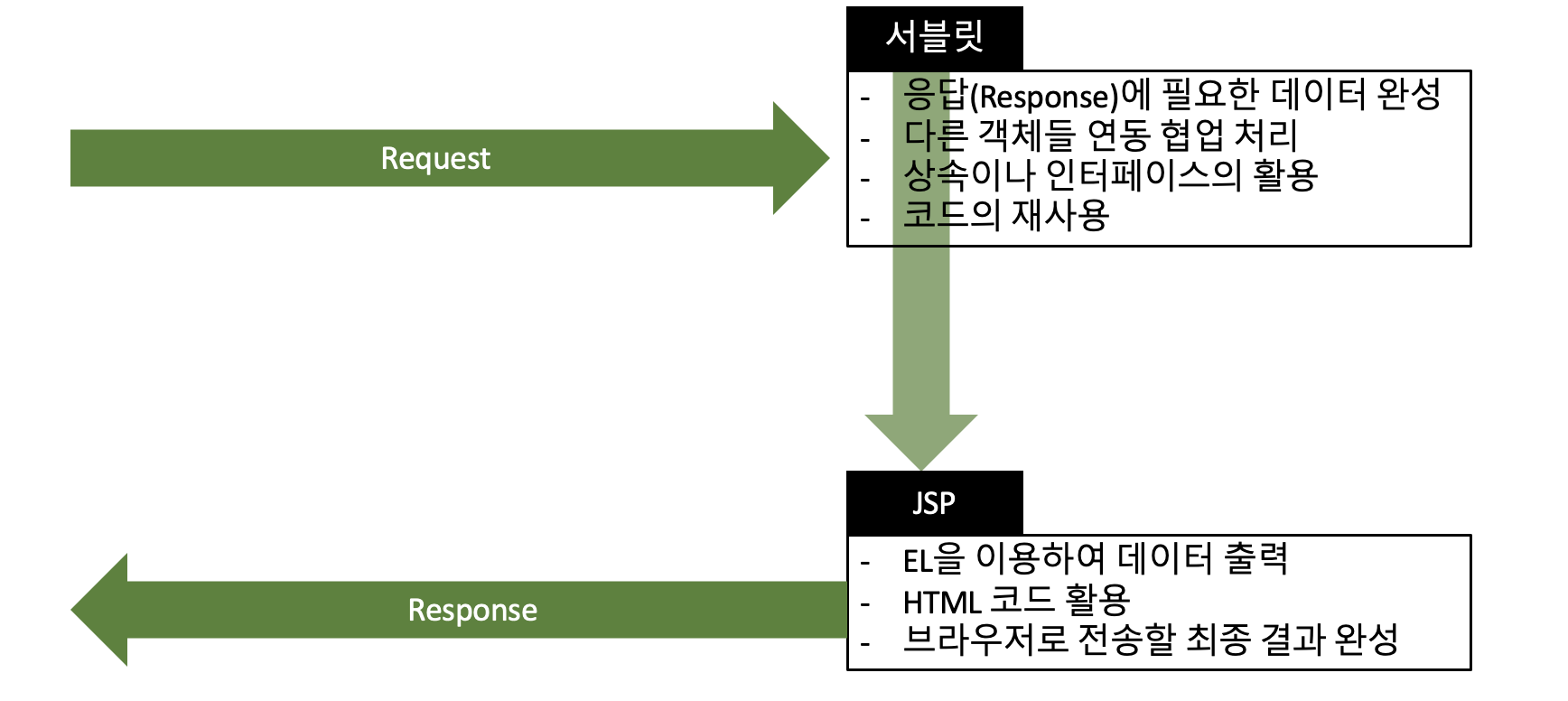
서블릿 코드의 경우, 자바 코드를 그대로 이용할 수 있다.(상속이나 인터페이스의 처리도 가능)하지만 서블릿 코드의 경우 HTTP로 전달된 메시지를 구성하는 HTML을 처리할 때는 상당히 많은 양의 코드를 작성해야 한다.JSP의 경우, 서블릿과 반대로 HTML 코드를 바
6.[알고리즘] 메타 용어_표준 용어 파싱

문제는 간단하다. 해당 원본 문자열이 주어지고, 그 문자열을 쪼갠 배열이 있다.그 배열의 모든 조합으로 원본 문자열로 만들어 각 배열의 요소 사이사이에 ('\_')를 넣어주면 된다.단, 정렬할 때 언더바를 기준으로 가장 첫 언더바 앞에 있는 배열의 요소가 긴 순서대로
7.[JQuery] 제이쿼리 반복문
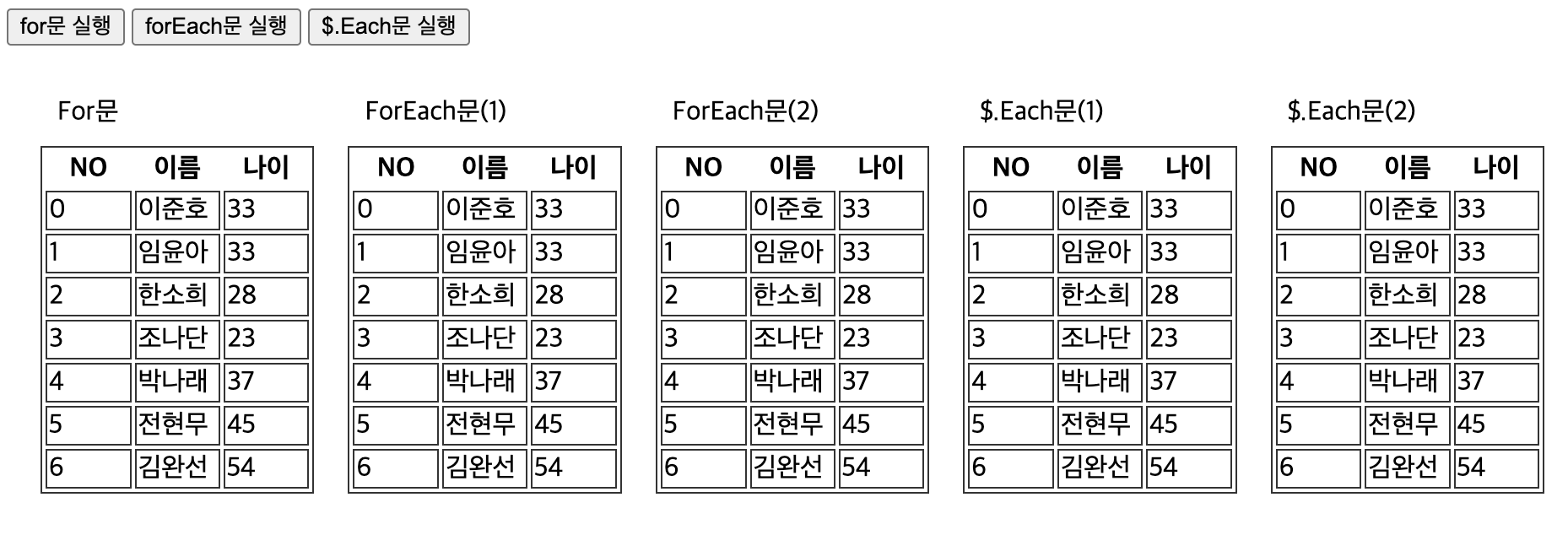
"항상 기본적이 반복문(for, foreach)만 쓰다가 오늘 jQuery반복문 존재에 대해 알게 되었다. 생소했기 때문에 정리하고자 한다." > ## 반복문(JQuery) 반복문 : 특정한 작업을 반복하는 것을 의미 예시
8.백트래킹 알고리즘 (BackTracking)
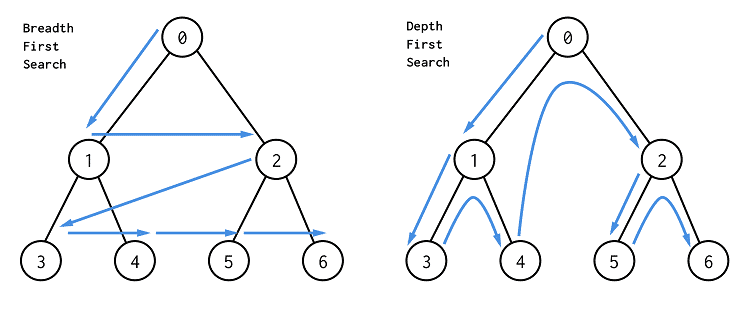
해를 찾는 도중 해가 절대 될 수 없다고 판단되면, 되돌아가서 해를 다시 찾아가는 기법을 말한다. (되추적) 깊이 우선 탐색으로 가능한 모든 경로를 탐색한다. (그래프에서 깊은 부분을 우선적으로 탐색)모든 경로를 탐색하는 특징으로 불필요할 것 같은 경로를 사전에 차단하
9.Linux | 리눅스 기본 명령어 정리

"리눅스" 윈도우와 맥 OS, iOS, Android 등은 모두 개발자가 아닌 사람들 즉, 사용자를 위해 만들어진 것으로, 가능한 어려운 조작없이 사용할 수 있는 거에 초점이 맞춰져 있다. 그렇기 때문에 위와 같은 OS들은 개발자가 프로그래밍을 하기에 제한적인 부분이
10.Linux | vi 편집기 명령어
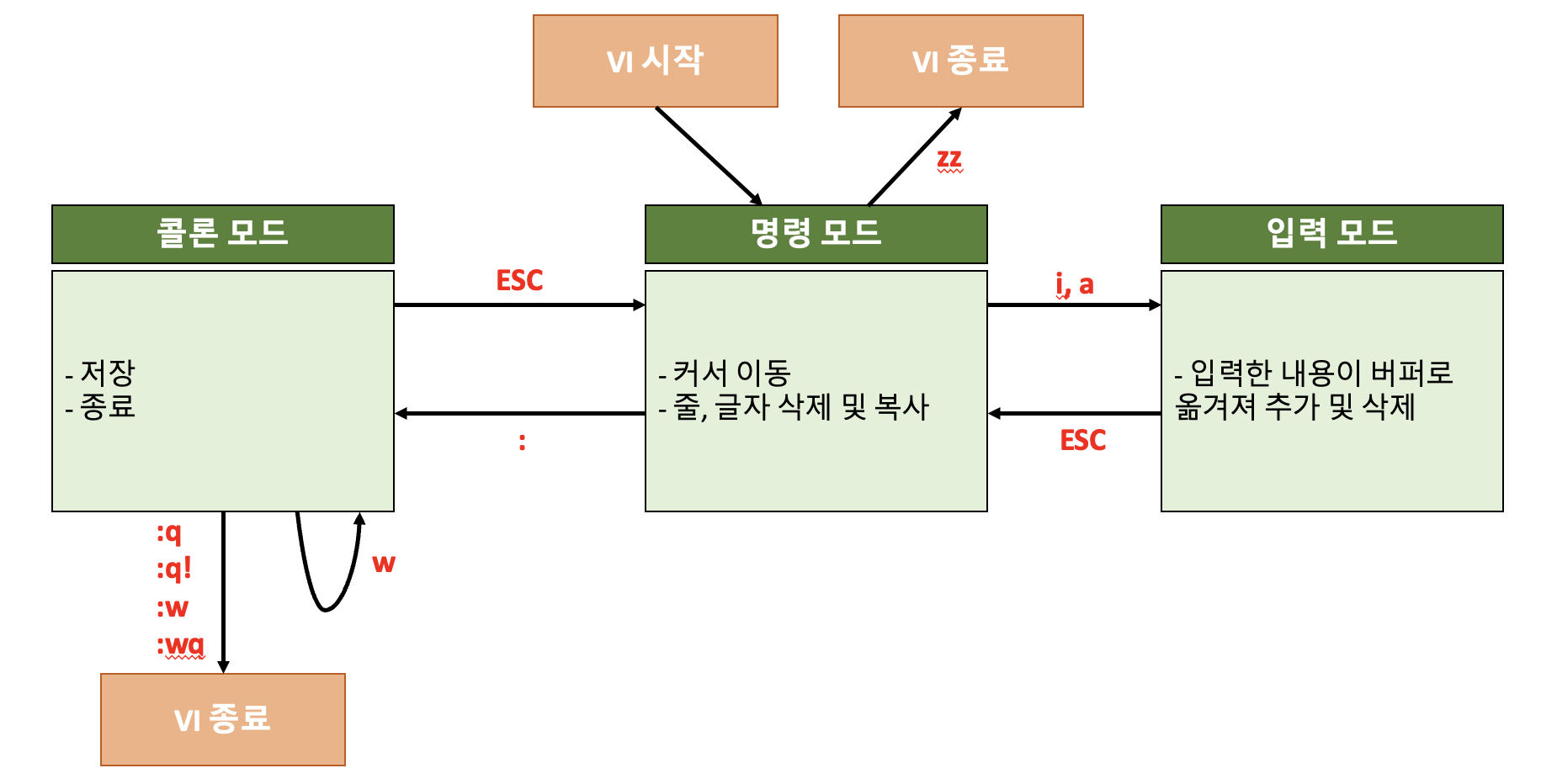
파일을 작성하거나 수정할 때 보통 편집기가 필요하다. 보통 집에서 컴퓨터를 쓸 땐 윈도우를 쓰거나 MacOS를 쓰는 경우가 많기 때문에 (메모장, Note와 같은) 편집기 명령어에 대해서는 생소할 수 있다. (저도 그랬으니...) 하지만, 리눅스환경에서는 기본 편집기로
11.Mac OS 에 PuTTY 설치

"이 POST는 homebrew가 설치되어 있다고 가정한 후 진행한다." 만약, 설치를 하지않았다면 아래의 링크에서 설치한 후 진행하길 바람. https://brew.sh/ Putty 설치 Mac Port 설치 Mac Port : macOS와 다윈 운영 체제의 소프
12.알고리즘 - 동적프로그래밍(Dynamic Programming)

백준 동적 프로그래밍 문제를 어느 정도 푼 후에 정리를 하게 되어 순서가 뒤죽박죽 된 느낌이지만...이대로 쭉 진행하면 이론을 완벽히 이해해서 문제를 푸는 느낌이 아니라 문제를 풀기 위해 공식을 넣는 느낌이라 풀면서도 '맞나...? 문제풀이를 더 진행하기엔 무리이지 않
13.Proxy - Proxy Server (1)

Proxy Or Proxy Server Proxy : 대리(행위)를 의미하는 단어 Proxy Server : 클라이언트(Client)와 서버(Server) 관점에서 중간에 대신 요청을 처리한다하여 클라이언트(Client)와 서버(Server)의 중계자 역할을 갖는 것
14.알고리즘 - 그리디 알고리즘(Greedy Algorithm)
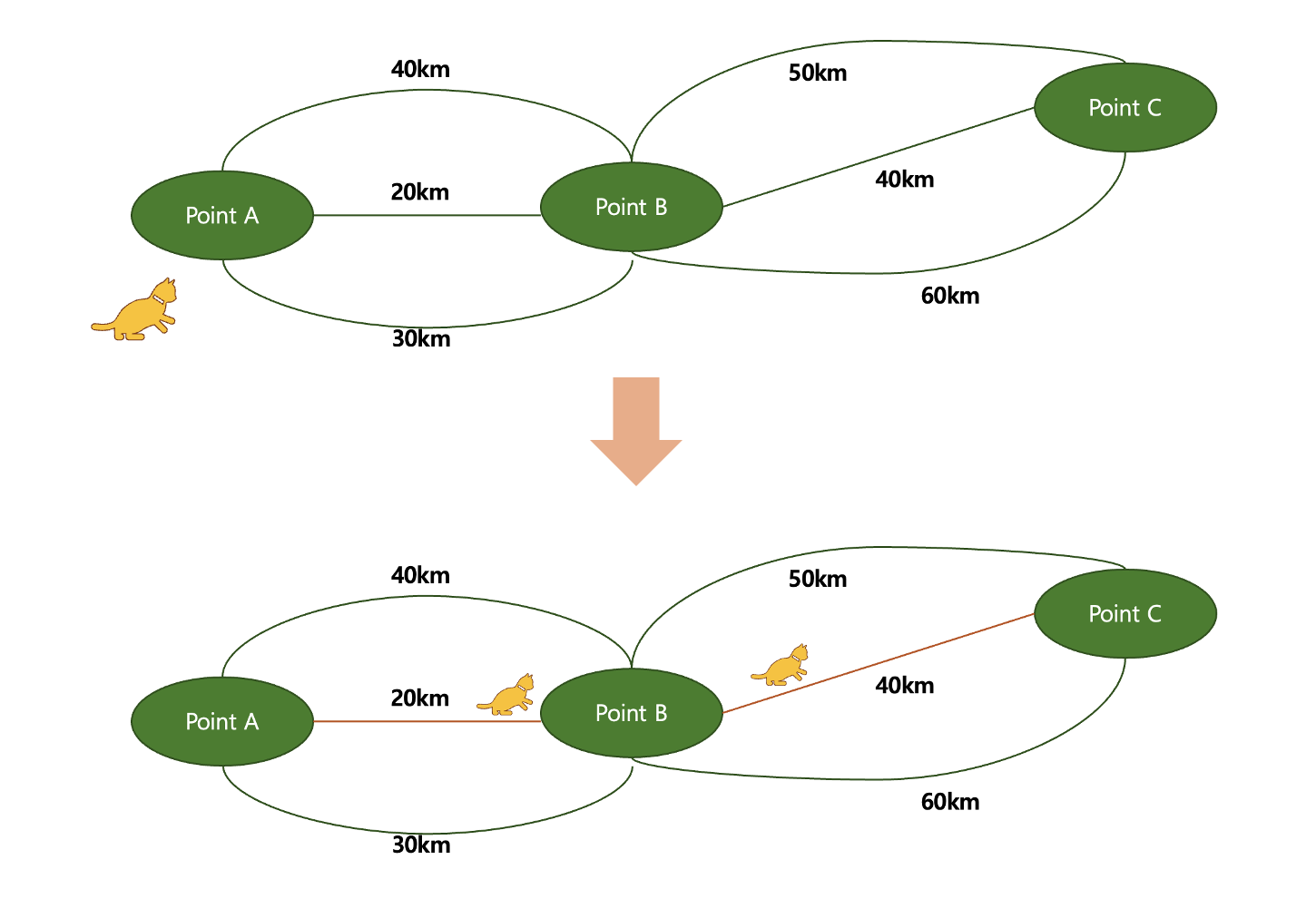
말 그대로 Greedy(=탐욕) 알고리즘으로, 현재 시점에서 가장 좋은 선택을 하는 알고리즘이다. 다시 말해서, 현 시점에서 선택한 것이 나중에 어떠한 결과를 초래하는지 고려하지 않는다고 말할 수 있다.그러한 특징으로 이 알고리즘은 항상 최적해를 보장하지 않는다.그림으
15.알고리즘 - 분할 정복 알고리즘(Divide and conquer algorithm)
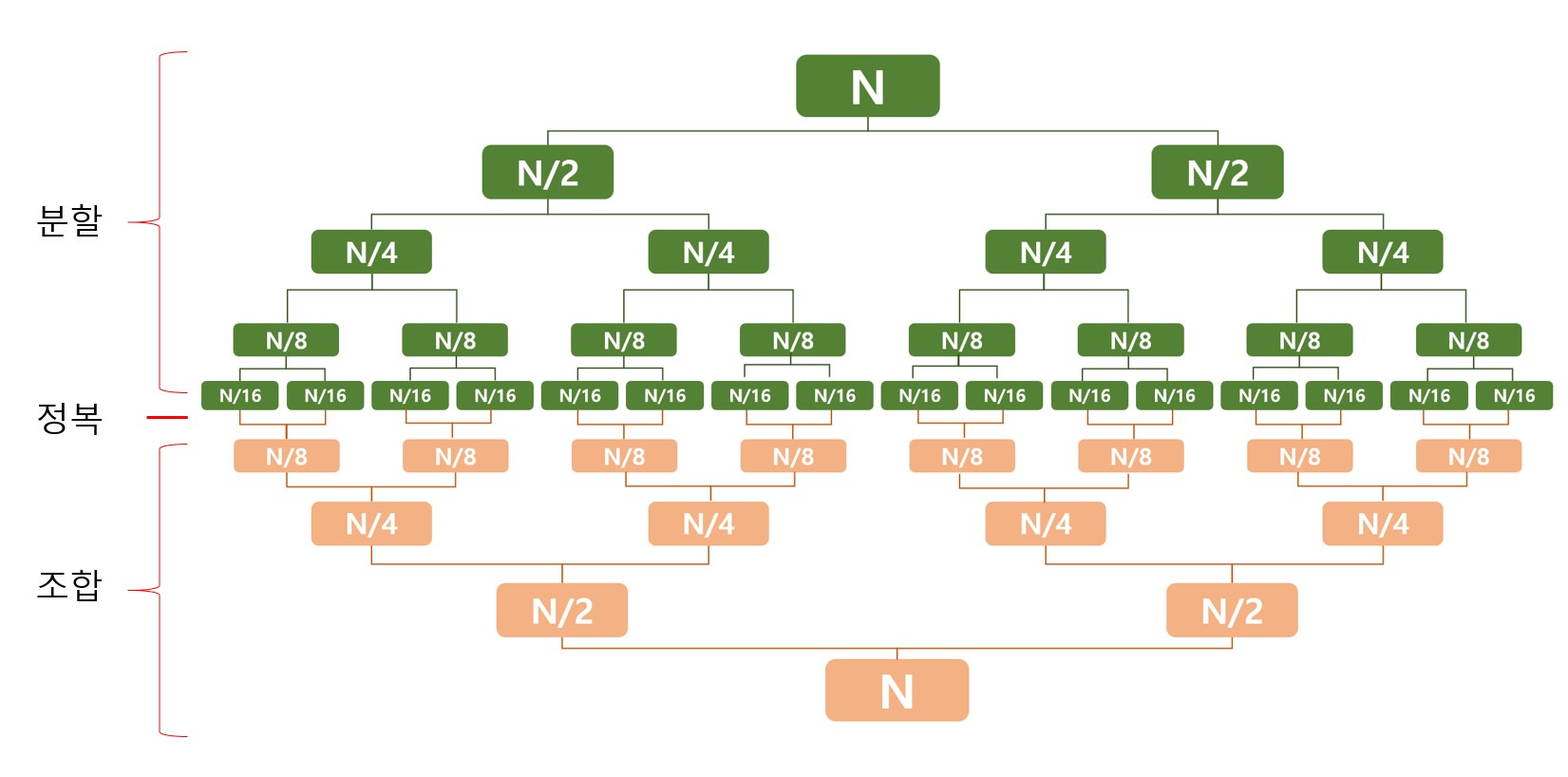
엄청나게 크고 복잡한 문제를 작고 단순한 문제로 조금씩 쪼개어 용이한(풀 수 있는) 문제가 되면 해당 문제를 풀어 다시 합치는 것을 말한다.다시 말해 분할 정복은 상단에서 분할하고 중앙에서 정복하며 하단에서 조합하는 형태를 가진다. \- 분할 : 문제를 더 이상
16.Docker(도커)를 사용하는 이유? (1)
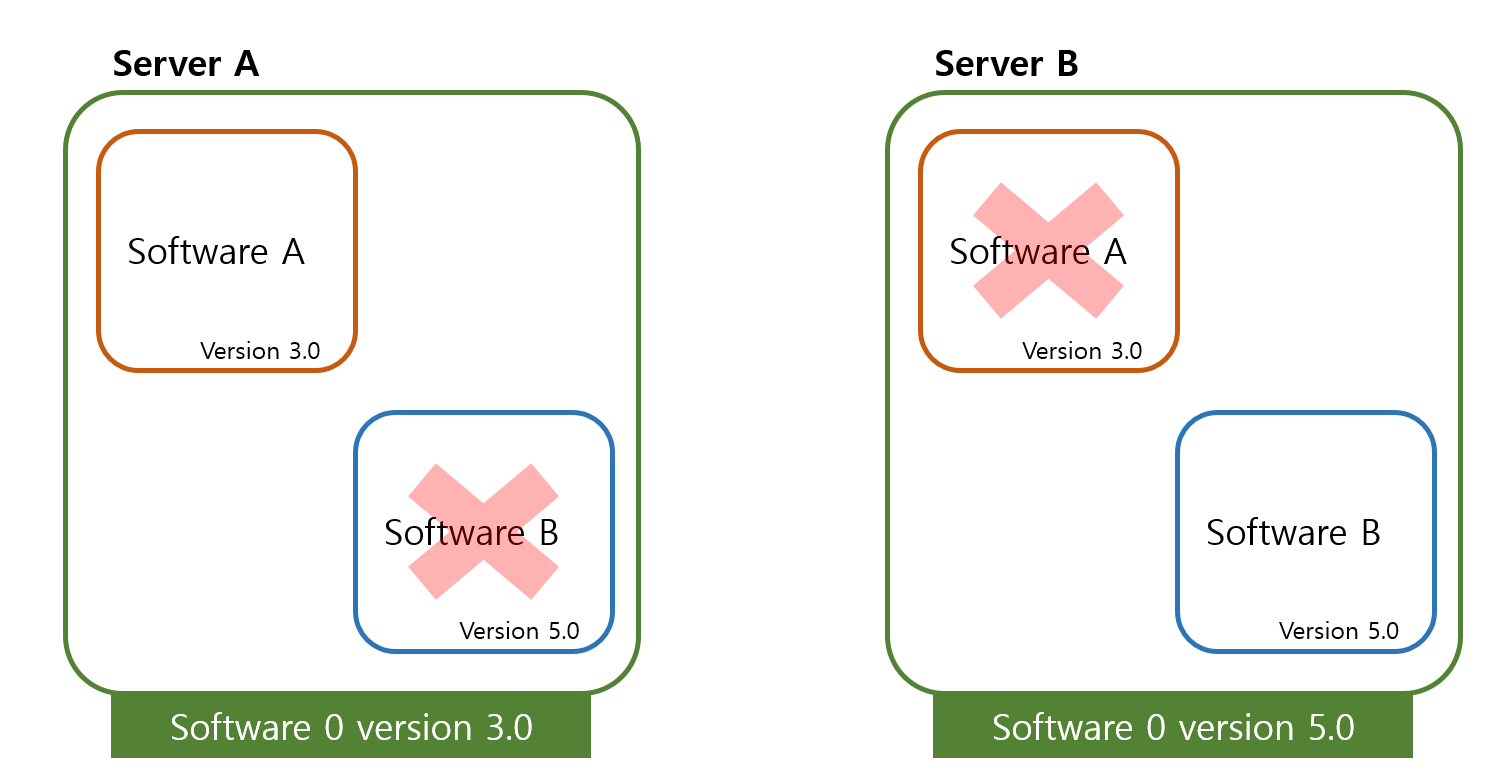
Docker(도커)에 대한 이야기는 익히 자주 들어서 '공부해야지..!' 매번 다짐했지만 미루고 미루다가 이제서야 정리할 기회가 와서 정리해본다:) 만약, 이 글에서 부족한 점이나 틀린 점이 있다면 댓글로 알려주시면 매우 감사할 것 같다..! (부탁드립니다🙇🏻♀️
17.Materialized View [MView]
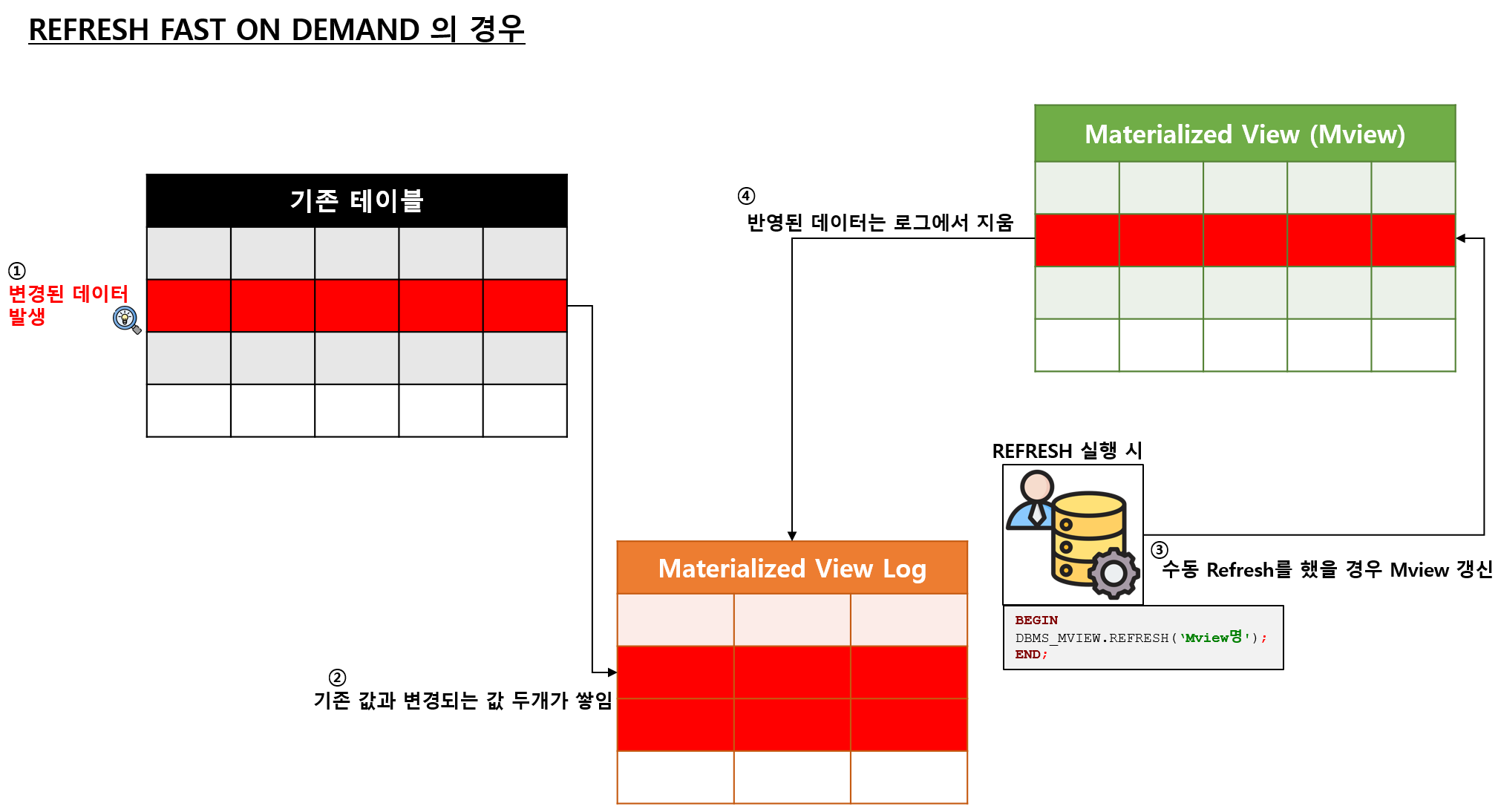
Materialized View는 데이터베이스에서 쿼리를 미리 계산하여 저장하는 물리적인 테이블이다. 복잡한 쿼리를 실행할 때 발생하는 성능 문제를 완화하기 위해 사용된다.