백준 11401 이항 계수 3

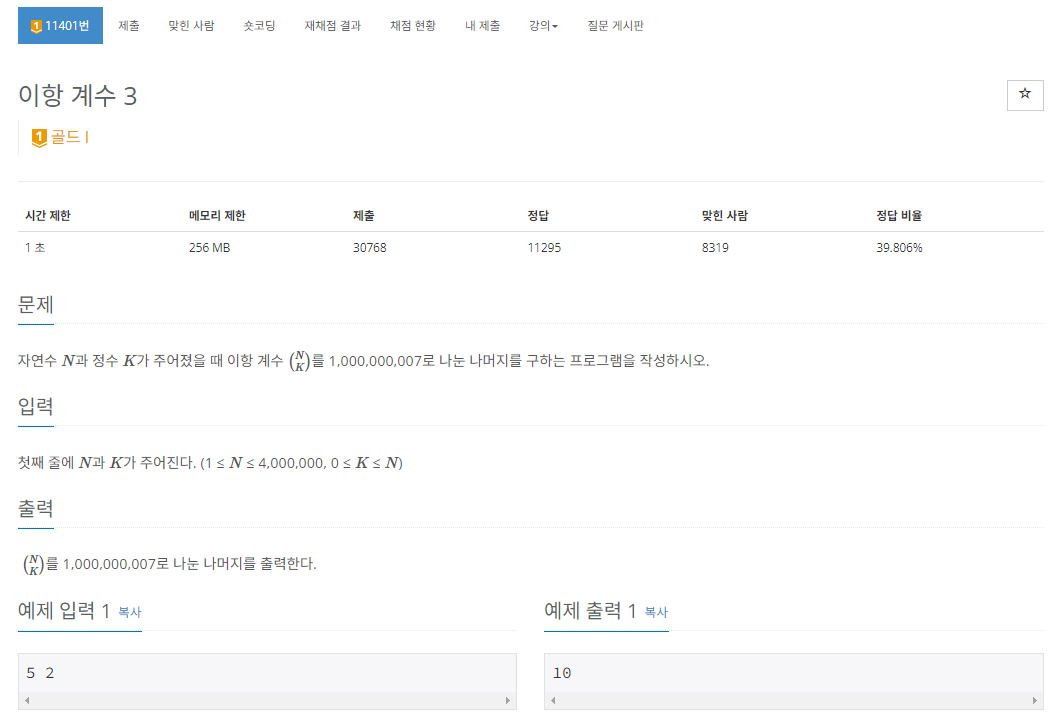
문제 해석

• 이항 계수1에서 설명했듯이 이항계수를 구하면 된다.
• 문제에서 나와있듯이 이항계수만 구해서 끝나는 문제가 아니라 1,000,000,007으로 나눈 나머지의 값을 구한다.
• 나머지를 구하기 위해 모듈러 연산을 사용해야하는데 , (n! / r! (n-r)!) % 1,000,000,007을 구할때 모듈러 연산은 나누기(/)로 분배법칙을 적용할 수 없다.
• 즉 분배법칙을 사용할 수 있는 방법으로 역수를 사용하면 되는 문제!
  
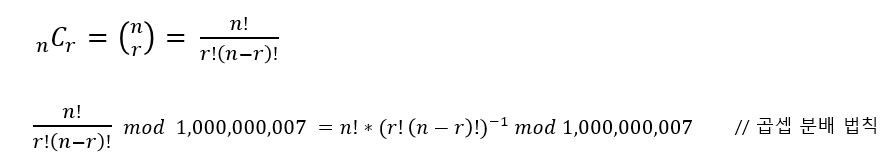
• 위와 같이 정리할 수 있지만, 지수 -1이라고 해서 분모가 분자가 되진 않는다. 이때 사용해야하는 것이 '페르마의 소정리'라고 한다.
• 페르마 소정리에 대한 정의는 페르마 소정리(내용과 증명)로 보면서 이해했기 때문에 따로 다시 정리하진 않겠다... (해당 블로그에서 잘 설명되어 있다!)
• 페르마 소정리를 이해했다면, 바로 식에 적용하는 것이 아니라 역원으로 한번 더 정리해야한다.
  
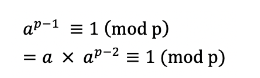
• 즉, a mod p 의 역원은 a^p-2 mod P이다.
• 위의 식에 역원을 적용하면 아래와 같다.
  
  

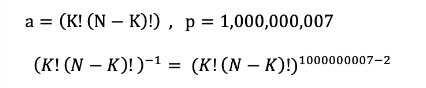
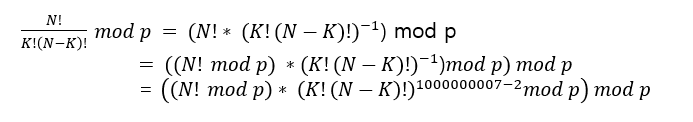
코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;


public class Main {

    final static long P = 1000000007; // 나누는 수

    public static void main(String[] args) throws IOException {
         BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
         StringTokenizer st = new StringTokenizer(reader.readLine(), " ");

         //이항계수 자연수 N과 정수 K =>NCK를 1000000007로 나눈 수를 구하면 됨.
         long N = Long.parseLong(st.nextToken());
         long K = Long.parseLong(st.nextToken());

         reader.close();

         long numerator =  getFatorial(N);  // 분자 (N!)
         long denominator = getFatorial(K) * getFatorial(N-K) % P; // 분모 ((K!*(N-K)!) mod P)

         //N! * 분모의 역원 (K!*(N-K)!)
        System.out.println(numerator * getPow(denominator, P-2) % P);

    }
    
    //팩토리얼 구하는 함수
    public static long getFatorial(long N) {
        long factor = 1L; //  초기 값

         while (N > 1){
             factor = (factor*N) % P;
             N--;
         }

         return factor;
    }

    //역원을 구하는 함수
    // 지수 밑의 수 num,  지수 exponent
    public static long getPow(long num, long exponent){
        long result = 1;

        while(exponent > 0){
            // 지수가 홀수면 result에 곱해주고,
            // 지수가 짝수라면 exponent가 1이 될때까지 밑의 수(num)를 제곱하다가 result에 담는다
            if(exponent % 2 == 1){
                result *= num;
                result %= P;
            }
            num = (num*num) % P;
            exponent /= 2;
        }

        return result;
    }


}

결과

느낀 점

페르마 소정리와 역원에서 멘붕이 왔다... 배운 적이 있었나 싶고,,, 사실 문제 푸는 방식에서 페르마 소정리와 역원을 사용해서 풀어나가야했기 때문에 해당 정리를 이해하느라 더 많은 시간이 걸렸다... (이런 문제만 계속 나오면 앞으로 어떻게 풀어야하는 거지,,,ㅜㅜ)