백준 1629 곱셈 [JAVA]

문제 해석

• 문제가 의미하는 바는 "첫째 줄에 A를 B번 곱한 수를 C로 나눈 나머지를 출력" 이게 다 이지만 시간 제한이 0.5초이므로 뭔가 간단하게 AXA...를 B번 곱해서 C로 진짜 나누는 문제는 아닐 것이다. (당연한거지만 ㅎ 실버 1문제가 그렇게 쉬울리가...)
• 아무튼 분할정복의 문제인 만큼 이 해설이 간단한 문제를 분할정복을 적용해서 풀어나가야 할 것이다.
  
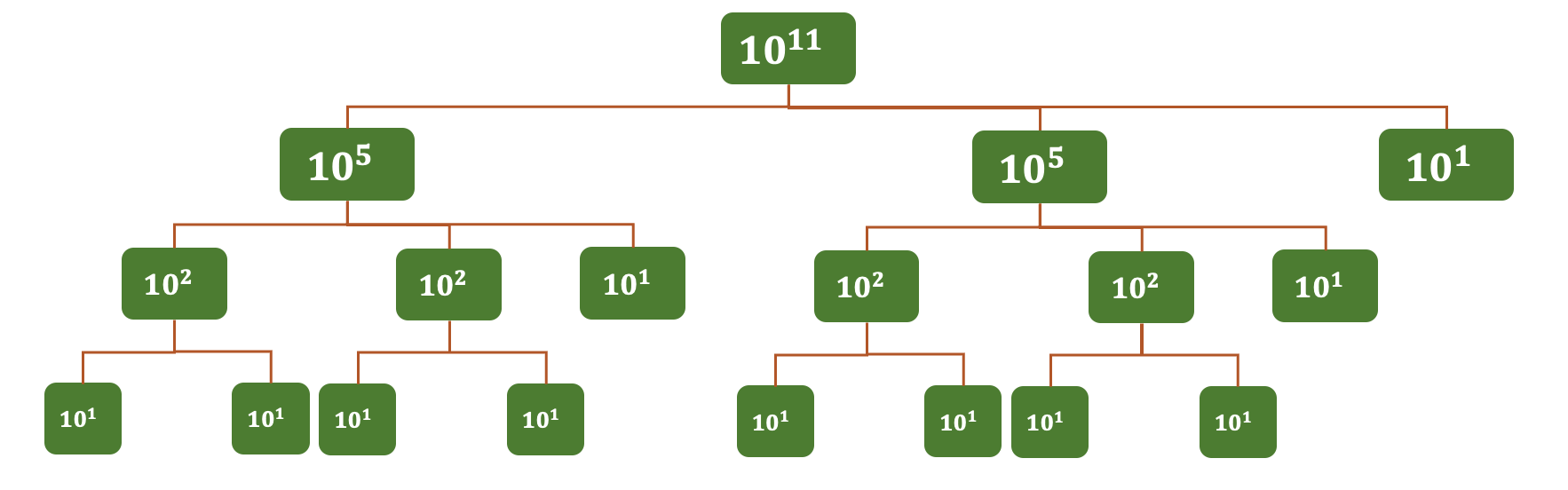
• 만약 10 11 12로 주어졌을 때 분할정복으로 표현하면 위와 같은 그림으로 구할 수 있을 것이다.
• 단, 이렇게 진행하면 10^3은 3번 구해야하고 10^2은 4번 구해야한다... 0.5초만에 결과를 뽑아내기에 숫자가 더 커지면 어려워질 수 있다. (구한 값은 재사용하는 방식으로 가야한다.)
  
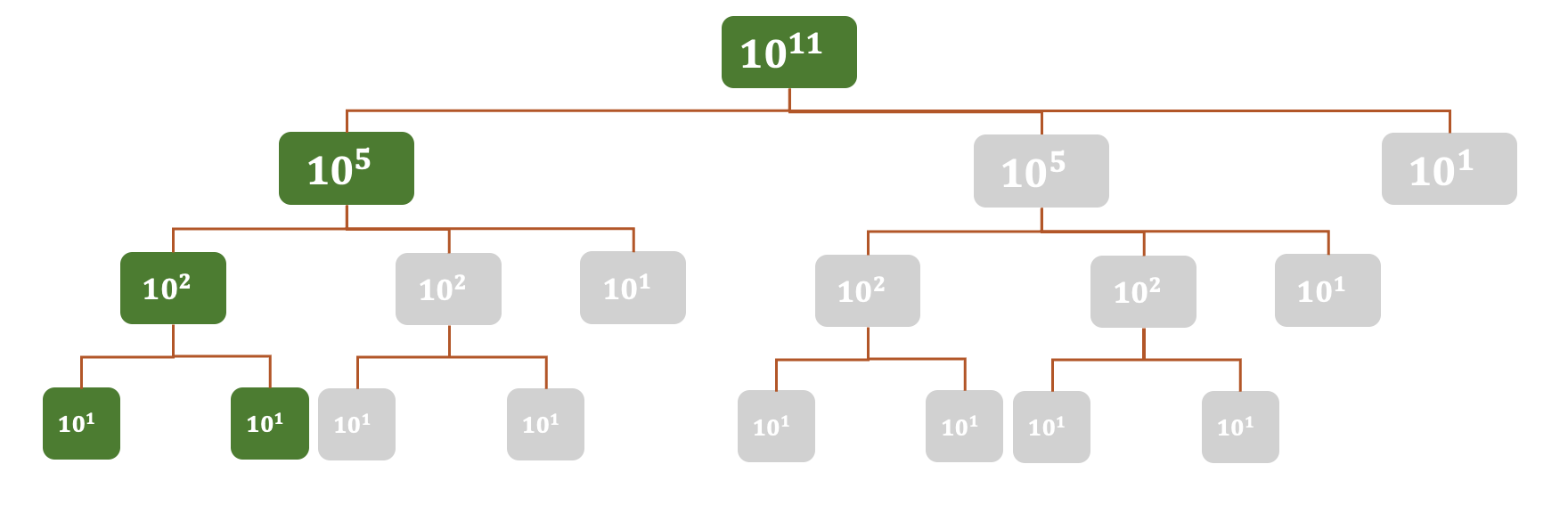
• 같은 라인의 값은 보통 같은 제곱의수를 포함하고 있다. 즉 왼쪽부터 탐색한다고 했을 때 왼쪽을 먼저 구한 후 같은 값을 곱해주면 된다는 의미이다. (짝수의 경우)
• 만약 홀수의 경우 10^2x10^2x10^1일 경우 10^2x10^2까진 짝수처럼 수행한 후에 10(^1)을 마지막에 곱해주면 된다.

// A의 exp승을 구하는 함수
public static long pow(long A, long exp) {

	//C는 나누는 수(예시에서의 12)

	if(exp == 1){ //exp가 1인건 A^1인 거니까 그대로
       	return A%C;
    }

	long value = pow(A, exp / 2);

	if(exp % 2 == 1) { //홀수의 경우
    	return (value * value % C) * A % C;
	}

	//짝수의 경우 
	return value * value % C;

}

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int C;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int A = Integer.parseInt(st.nextToken()); //주어진 수
        int B = Integer.parseInt(st.nextToken()); //몇승인지
        C = Integer.parseInt(st.nextToken()); //나눠야 하는 수

        System.out.println(pow(A, B));
    }

    //A의 exp승 구하는 함수
    private static long pow(int A, int exp){
        if(exp == 1){
            return A%C;
        }

        //exp 절반한 값을 구한다.
        long value = pow(A, exp/2);

        /*
            문제 해석에서는 넣지는 않았지만 아래에 나온 공식은 모듈러공식으로
            (AxB)modC = ((AmodC)X(BmodC))modC
            => (A*B)%C =  ((A%C)*(B%C))%C
                       = ((AxB)%C)%C 인 것을 알 수 있다.
        */
        if(exp % 2 != 0){ //만약 지수가 홀수이면
            return (value*value%C)*A%C;
        }

        //짝수의 경우
        return value*value%C;
    }
}

결과

느낀 점

• 분할정복 문제임을 알아서 그냥 일단 나누고 보자하는 방식으로 풀어서 푸는데 큰 어려움이 없었지만 만약 문제만 덩그러니 주어졌을 때 분할정복을 떠올릴 수 있을까가 의문이 드는 문제였다... (아직 멀었다는 뜻..)