문제 해석
- 배낭 알고리즘(Knapsack)은 물건을 쪼갤 수 있는 Fraction Knaspack Problem과 물건을 쪼갤 수 없는 0-1 knapSack Problem으로 나뉘는데 이번 백준 12865 평범한 배낭 문제는 0-1 knapSack Problem에 해당하는 문제이다. (물건을 쪼갤 수 없는 구조!)
- 이번 문제 또한 글로 정리하기 어려운 문제이니 그림으로 정리하자면 아래와 같다. (일단, 문제의 예시처럼 물건은 총 4개이고 배낭에 넣을 수 있는 최대 무게는 7이다.)
각각의 물건은 아래와 같은 값을 가진다.
물건 1번 무게 6, 가치는 13
물건 2번 무게 4, 가치는 8
물건 3번 무게 3, 가치는 6
물건 4번 무게 5, 가치는 12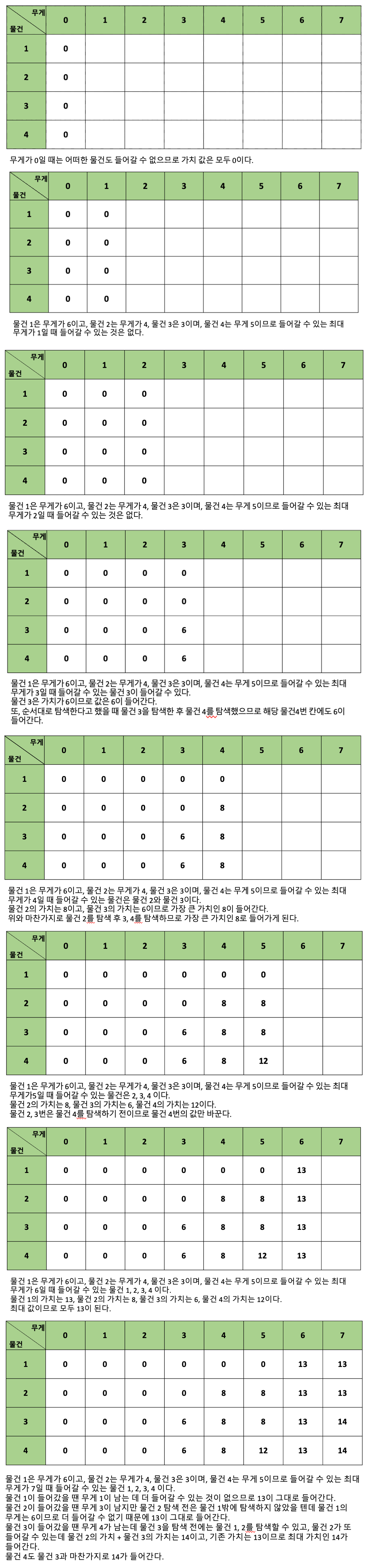
- 위의 과정을 정리하면 아래와 같다
knapSack(i, k) i가 물건 번호고, k는 최대 무게이다.
if 물건의 번호가 0미만이고, 배낭에 들어가는 최대 무게가 0일때
0
if 배낭에 들어가는 최대 무게 < 입력된 무게
knapSack(i-1, k)
if 물건의 번호가 0보다 크고, 배낭에 들어가는 최대 무게 >= 입력된 무게
max(knapSack(i-1, 최대 무게-입력(현재)된 무게)+현재 가치, knapSack(i-1, k))
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
static int[] W; //무게 배열
static int[] V; //가치 배열
static Integer[][] dp; //무게(열)와 물건(행)로 작성했던 그 테이블을 표현한 배열
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); //물건 개수
int K = Integer.parseInt(st.nextToken()); //배낭에 들어갈 수 있는 최대 무게 값
W = new int[N];
V = new int[N];
dp = new Integer[N][K+1];
for(int i = 0; i < N; i++){
st = new StringTokenizer(br.readLine());
W[i] = Integer.parseInt(st.nextToken());
V[i] = Integer.parseInt(st.nextToken());
}
System.out.println(knapSack(N-1, K));
}
//최대 부분 문자열 길이 구하기(i : 물건 번호, k : 들어갈 최대 무게)
static int knapSack(int i, int k){
//물건 번호가 범위 밖일 때
if(i < 0)
return 0;
if(dp[i][k] == null){ //탐색하지 않았다면,
//현재 물건 i를 추가로 못담는 경우(무게 초과일 경우)
if(W[i] > k) {
//이전 값을 넣는다.
dp[i][k] = knapSack(i - 1, k);
}
else{ // 현재 물건 i을 담을 수 았는 경우
// 이전 i값과 이전 i값에 대해 가치 값 + 현재 물건 i의 가치 값 중 큰 값을 저장
dp[i][k] = Math.max(knapSack(i-1, k), knapSack(i-1, k-W[i]) + V[i]);
}
}
return dp[i][k];
}
}결과

느낀 점
유명한 알고리즘 문제라고 하나... 나에겐 처음 보는 알고리즘이라 문제 이해하는 데 꽤 오랜 시간이 걸렸다... 그래도 풀어내긴 했으나 아직 부족한 게 많다😭
