백준 9251 LCS [JAVA]

문제 해석

• 이 문제는 말로 설명하기 어려운 문제인 것 같아서 바로, 예시로 흐름을 보여주고자 한다.

• 그전에 이 문제를 생각했을 때의 규칙을 아래와 같이 설정했다.
  LCS - 최장 공통 부분 수열 사이트를 보고 이해했다...
  
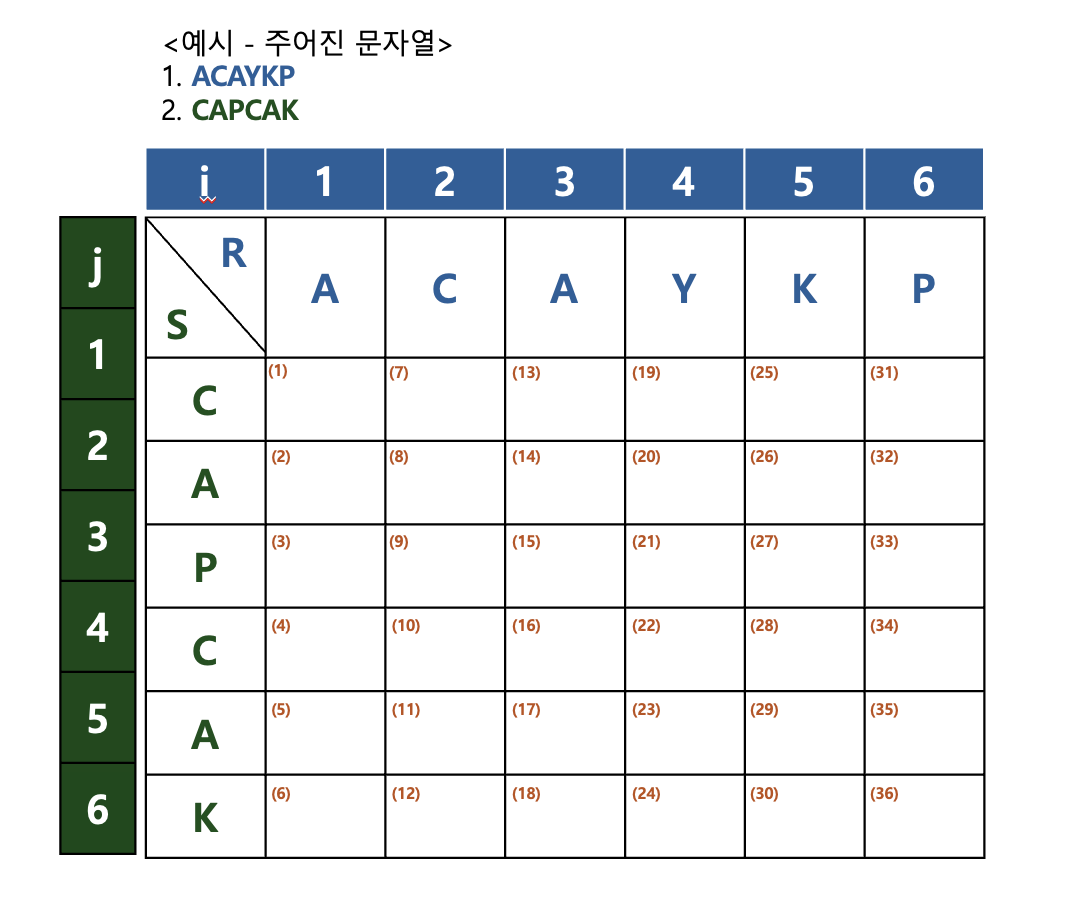
  1. R[i] 과 S[j]이 가지고 있는 초기값은 Ø(=공집합)이다.
  2. R[i] 과 S[j]의 각각의 문자가 서로 같다면 해당 문자를 해당 자리의 값과 추가한다.
  3. R[i] 과 S[j]의 값이 서로 같지 않으면 그 전의 위치인 R[i-1], S[j] or R[i], S[j-1]값 중 가장 긴 값을 넣는다.

• 예시를 가지고 설명하면 아래의 흐름과 같다.
  

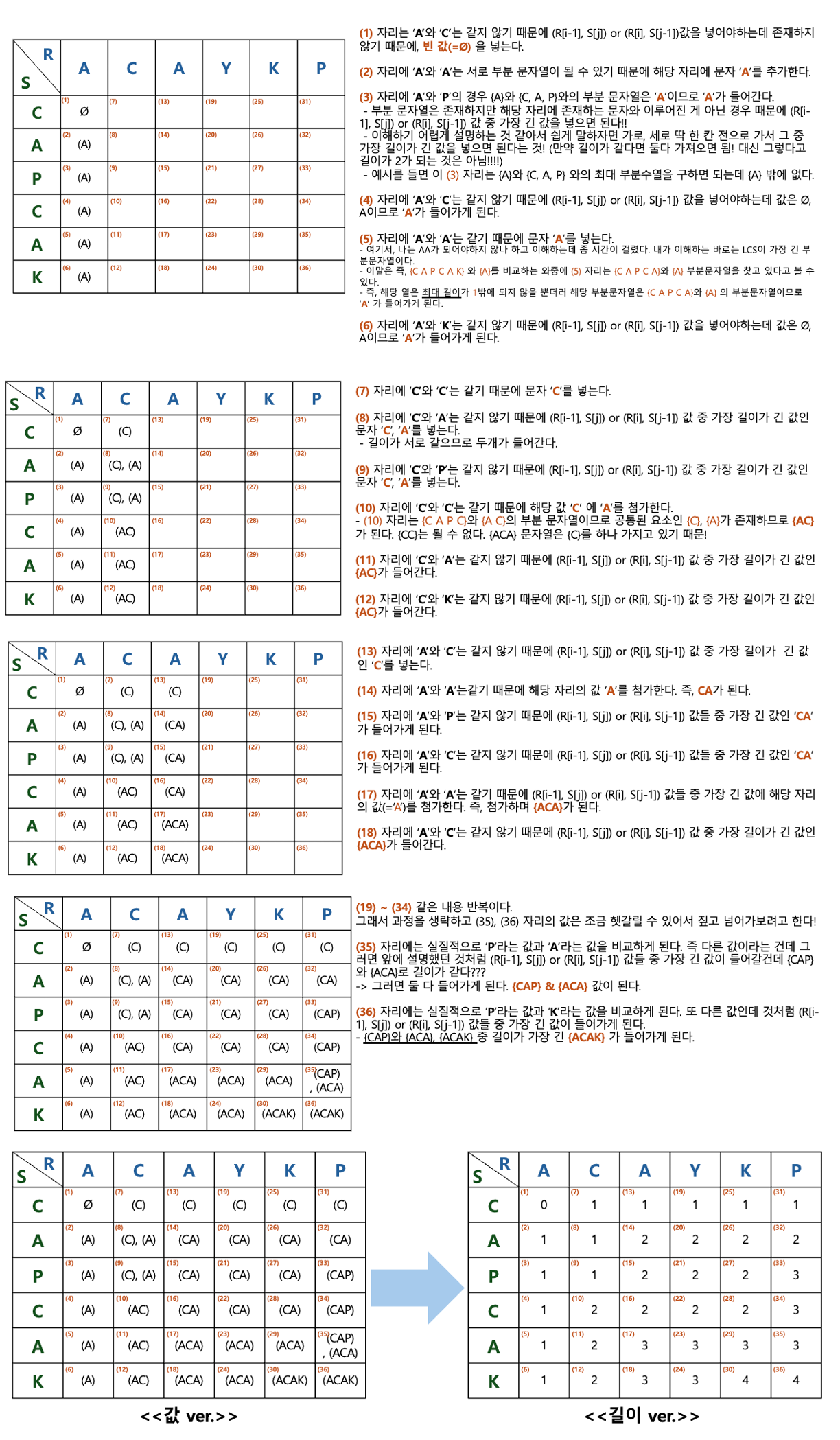
• 위의 사진을 천천히 읽고 흐름을 잘 따라왔다면 해당 규칙을 식으로 표현할 수 있을 것이다.

만약,Ri와 Sj가 같다면,
LCS(Ri, Sj) : LCS(Ri-1, Sj-1) + 1     

만약,Ri와 Sj가 다르다면,
LCS(Xi, Yj) : max( LCS(Ri-1, Sj), LCS(Ri, Sj-1))     

• 이 규칙을 사용하여 코드를 작성하면 된다!

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;

public class Main {

    static char[] RArr; //R 배열
    static char[] SArr; //S 배열
    static Integer[][] dp; //R(열)와 S(행)로 작성했던 그 테이블을 표현할 배열!

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        //문자열 입력 받기
        String RStr = br.readLine();
        String SStr = br.readLine();

        //배열 문자열의 길이만큼 초기화
        RArr = new char[RStr.length()];
        SArr = new char[SStr.length()];

        //RXS 크기 만큼의 이차원배열 초기회
        dp = new Integer[RStr.length()][SStr.length()];

        //문자열을 하나하나 쪼개서 배열에 넣기(단위 : 문자)
        RArr = RStr.toCharArray();
        SArr = SStr.toCharArray();

        //해당 인덱스가 0부터 시작하므로 -1을 한 값을 넣어준다.(각각의 길이)
        System.out.println(LCS(RStr.length()-1, SStr.length()-1));
    }

    //최대 부분 문자열 길이 구하기
    static int LCS(int RIndex, int SIndex){
        if(RIndex == -1 || SIndex == -1){ //공집합을 가리킬 경우(존재하지 않은 값일 경우)
            // 이 조건식 빼면 에러가 생길 수 있음(=outbound error??)
            return 0;
        }

        if(dp[RIndex][SIndex] == null){ //탐색하지 않은 자리일 경우
            if(RArr[RIndex] == SArr[SIndex]){ //만약 해당 자리가 같은 값일 경우 해당 자리값을 추가한다. 즉 길이 +1
                dp[RIndex][SIndex] =  LCS(RIndex-1, SIndex-1) +1;
            }else{ //해당 자리의 값들이 서로 다른 값일 경우 R(i-1), S(j) 의 값과 R(i), S(j-1)의 값 중 긴 값의 길이를 넣으면 된다.
                dp[RIndex][SIndex] =  Math.max(LCS(RIndex-1, SIndex), LCS(RIndex,SIndex-1));
            }
        }

        return dp[RIndex][SIndex];
    }
}

결과

느낀 점

이 문제 해석하는 데만 진짜 오랜 시간이 걸렸다... LCS를 찾아보니 길이로만 표시해놓은 곳이 많아서 사실 더 이해하기 어려웠다. 아마 나 같은 분이 있으실 수 있을거라 생각해서 열심히 과정을 적어놓았는데 맞게 잘 설명한지는 모르겠다🥹..
아무튼! 오래 이 문제를 보고 있어서인지는 몰라도 풀고 나니 뿌듯하다...🫣