백준 13241 최소공배수[JAVA]

문제 해석

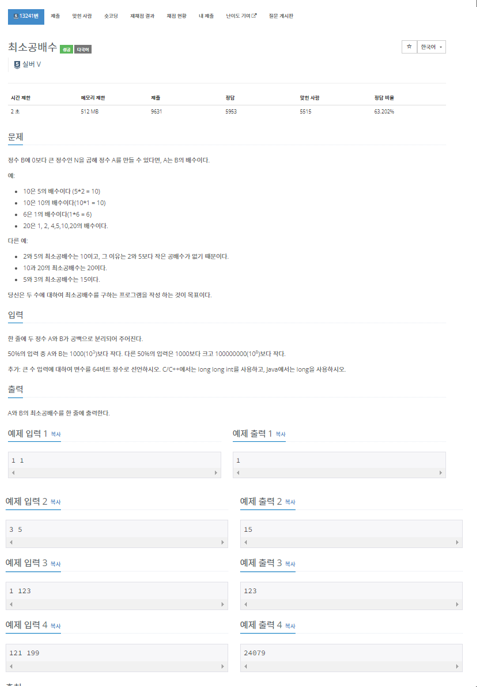
• 두 자연수 A와 B를 입력받아서 최소공배수를 구하면 되는 문제이다.
• 단, 50%의 입력 중 A와 B는 1000(10³)보다 작다. 다른 50%의 입력은 1000보다 크고 100000000(10⁸)보다 작기 때문에 최대 공배수를 구할 때 AxB/최대공약수 의 공식을 사용하는데 int를 그대로 쓰면 에러가 날 수 있다.
• 따라서, long을 써야 한다.

코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        long A = Integer.parseInt(st.nextToken()); //정수 A
        long B = Integer.parseInt(st.nextToken()); //정수 B

        br.close();

        if(A > B){ //A가 클 경우
            bw.write(A*B/findGCD(A, B) + "\n"); 
        }else if(A < B){ //B가 클경우
            bw.write(A*B/findGCD(B, A) + "\n");
        }else{ //A와 B가 같을 경우
            bw.write(A + "\n"); //둘이 같다면, 하나만 출력하면 된다.
        }

        bw.flush();
        bw.close();
    }
    
    //최소 공배수 찾는 메서드
    static long findGCD(long A, long B){
        while(B != 0){
            long R = A%B; //나머지
            A = B; 
            B = R;
        }
        return A;
    }
}

• 코드 자체는 A와 B의 크기 비교를 제외하고는 전 포스트-1934 최소공배수[JAVA]와 동일하다.

결과

느낀 점

• 확실히 전에 최소공배수와 최대공약수 구하는 알고리즘에 대해 이해를 하고 이 문제를 직면해서 큰 어려움이 없었다.