문제 해석
-
첫번째 줄에는 입력받을 두 자연수(A, B)쌍의 개수(T)을 입력받아 두 자연수(A, B)의 쌍의 개수(T)만큼 입력받는
다. -
두 자연수(A, B)쌍의 개수(T)개 만큼 입력받았다면 각각의 두 자연수(A, B)의 최소 공배수 각각 구하면 된다.
-
최소 공배수란 두 수에 서로 공통으로 존재하는 배수 중 가장 작은 수를 의미한다.
-
보통, 최소 공배수를 구하는 방식은 A의 약수를 모두 구하고, B의 약수를 모두 구해서 공통된 약수들만 서로 곱해주면 된다.
-
하지만, 이러한 경우는 어떤 수가 클 경우 그것을 인수분해하는데 시간이 너무 많이 소요된다는 것이다.(두수의 공통 약수를 모두 찾아 다시 곱해줘야하는...)
-> 이러한 문제점을 해결하기 위해 나온 최대공약수 or 최소공배수를 사용하기 위한 알고리즘을 방식이 유클리드 호제법이다.
정리

- 최대공약수와 최대공배수는 보통 이렇게 구한다.
- 앞서 설명한 것처럼 이러한 방식은 주어진 자연수가 클 경우 인수분해하는데에 시간이 많이 소요되며, 인수분해가 완료되었다고 하더라도 다시 공통약수를 곱하는데에 시간도 많이 소요된다.
유클리드 호제법이란 무엇인가?
-
큰 수를 작은 수로 나눈다.
-
나누는 수를 나머지로 계속 나눈다.
-
나머지가 0이 나오면 나누는 수가 최대공약수이다.
유클리드 호제법의 원리
- GCD(A, B) = GCD(B, R)공식을 증명해야한다.
- GCD(A, B) => A mod B = R이기 때문에 A = Q(몫)xB + R(나머지)라고 할 수 있다.
- 그렇다면, R이 최대 공약수를 가지고 있다는 것을 증명을 해야하는데...
- A와 B의 두 자연수의 최대공약수를 G라고 가정했을 때,
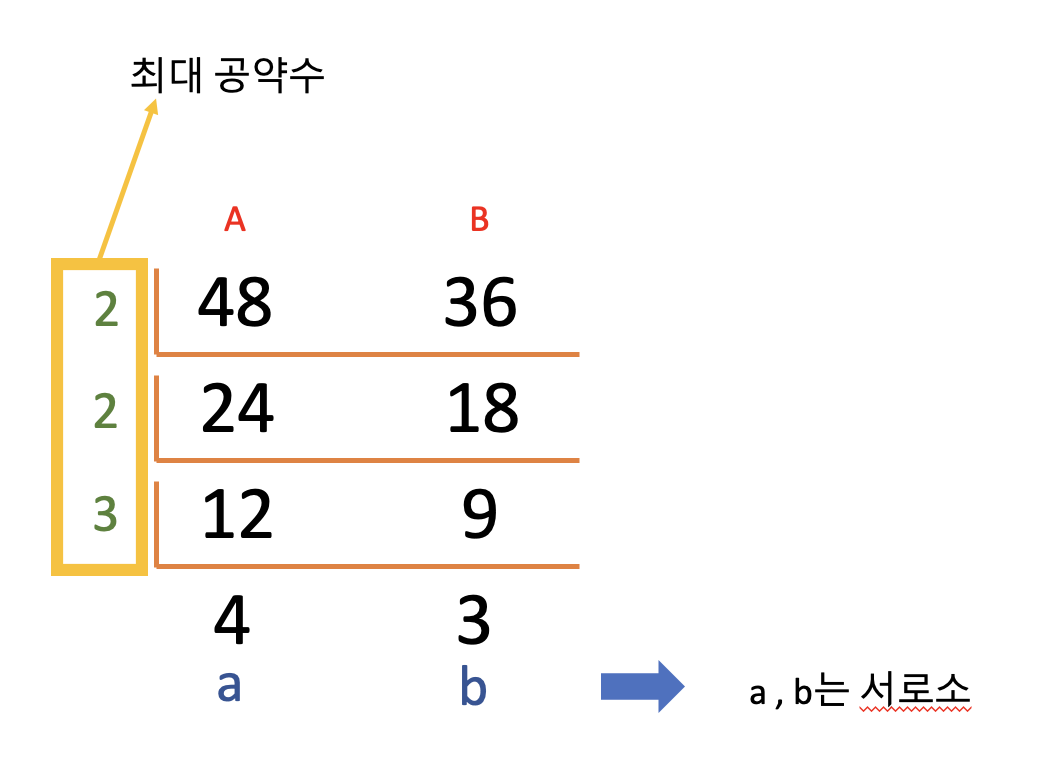
- A = axG라 할 수 있고, B = bxG라 할 수 있다.
- 위의 식으로 R을 구하면,
- 일단 A = QxB + R이라고 했고, A = axG니까, axG = QxB + R, 또, B = bxG니까, axG = QxbxG + R이다.
- 그렇다면, R = axG - QxbxG이고 공통으로 가지고 있는 G로 묶으면, R = (a - Qxb)xG가 된다.
- 식을보면 R 또한 G(최대 공약수)를 가지고 있는 것을 확인할 수 있다. 즉, B와 R의 최대 공약수가 곧 A와 B의 최대 공약수이다.
그렇다면, 최소 공배수는 어떻게 구할까?
- 최대 공약수 원리를 이해했다면 여기서부턴 쉽다.
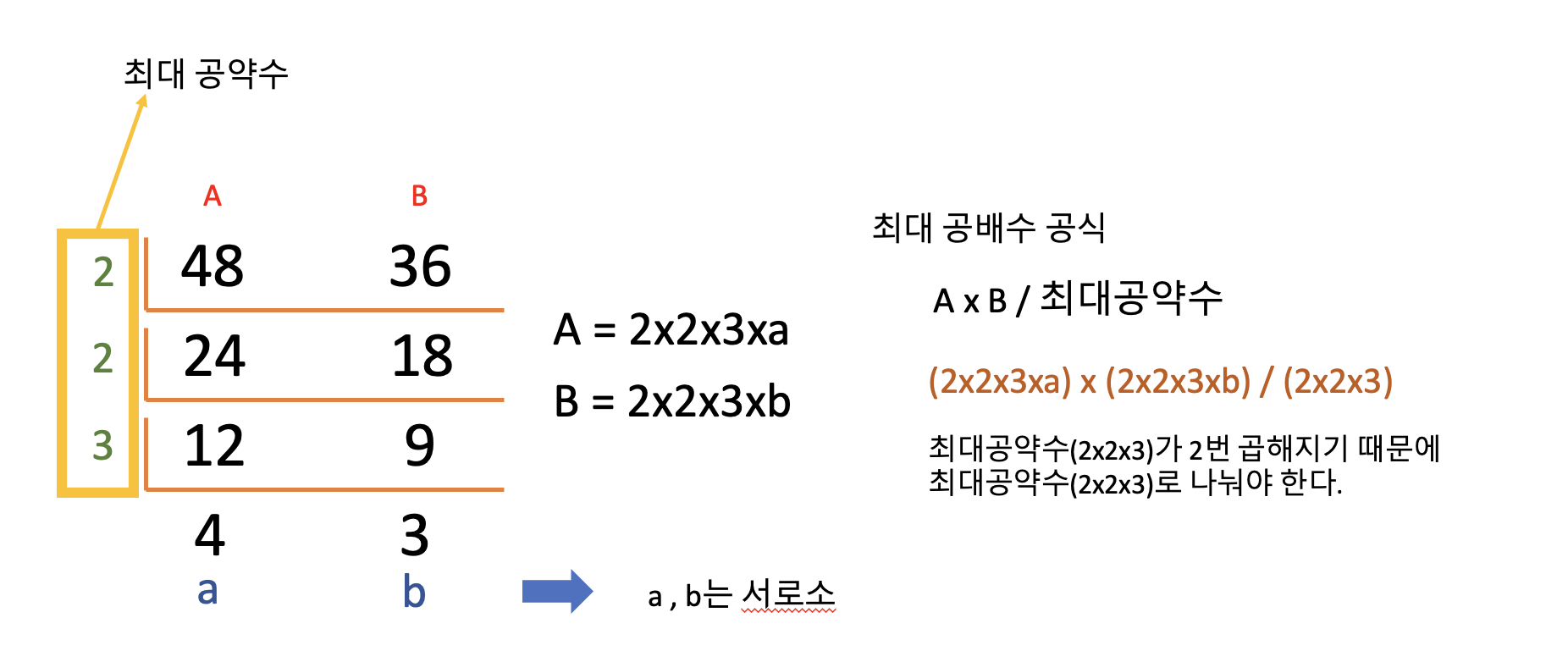
- 즉, 최대공약수를 구했다면 A*B/최대공약수를 하면된다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for(int i = 0; i < T; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
bw.write(A*B/findGCD(A, B) +"\n");
}
br.close();
bw.flush();
bw.close();
}
//최대 공약수 구하기
static int findGCD(int A, int B){
/*
GCD(A, B) = GCD(B, R) = GCD(R, R1) = GCD(R1, R2) = ... = GCD(Rn, 0)
=> Rn이 최대 공약수
*/
while(B != 0){ //B가 0이 되기 전까지 반복(나머지가 0일때까지)
int R = A%B; //나머지 저장
A = B; //B를 A에 저장
B = R; //A에 B를 저장
}
return A;
}
}결과

느낀 점
- 처음에 최소공배수를 구하는데에 급급하여 최대 공약수를 구하는 공식을 생각조차 하지 못하여 어려움이 존재하였지만, 이번기회에 최대공약수를 구하는 공식을 이해할 수 있었다.
