🤔 알고리즘 성능 표현 방법?
알고리즘은 풀다가 시간복잡도와 공간복잡도에 대해 들어본 적이 있으신가요? 오늘 주제인 알고리즘 성능 표현 방법이 바로 시간복잡도와 공간복잡도입니다.
알고리즘을 평가 하는데 있어 수행시간과 메모리로 사용량을 기준으로 둡니다.
- 수행시간에 해당하는 것이 시간복잡도
- 메모리 사용량에 해당하는 것이 공간복잡도
📝 성능 표현을 표기하는 방법?(feat. Big O)
알고리즘 성능 표현 방법을 조금 더 간편하게 할 목적으로 표기하는 방법이 있습니다. 그게 바로 Big O 표기법 입니다.
앞서 말했듯이 알고리즘의 효율성을 표기해주며 보통 알고리즘의 시간복잡도오 공간복잡도를 나타내는데 사용합니다.
Big O 표기법의 규칙
- 가장 높은 차수만 남긴다
O(n² + n) -> O(n²)- 계수 및 상수는 과감하게 버린다
O(2n + 3) -> O(n)대표적인 Big O 표기법
- O(1)
: 입력 데이터의 크기와 상관없이 언제나 일정한 시간이 걸림 - O(n)
: 입력 데이터의 크기에 비례해서 처리시간에 걸림 - O(log(n)
: 로그의 특성에 따라 데이터 양이 많아져도, 시간이 조금씩 늘어납니다. 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형 - O(n^2)
: 데이터양에 따라 걸리는 시간은 제곱에 비례합니다.
이렇게만 보면 이해가 잘되지않으니 그래프를 함께 봐봅시다!
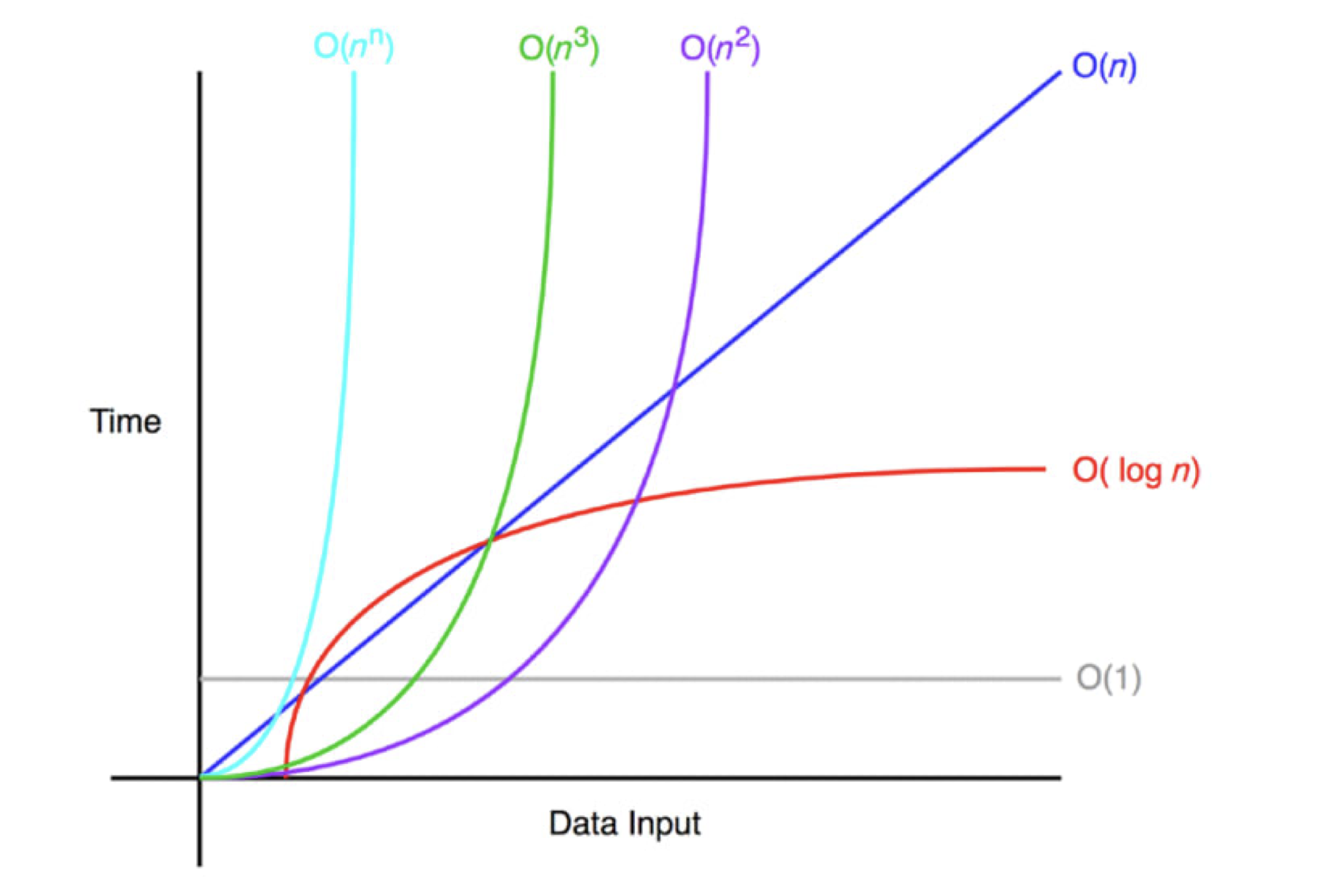
이렇게 시간복잡도와 공간복잡도를 알아보기 전에 기초적인 표기법에 대해서도 알아봤으니까 본격적으로 설명을 시작해보겠습니다.
⏱ 시간복잡도
시간복잡도란 알고리즘이 문제를 해결하기 위한 시간의 횟수, 입력 값의 개수와 알고리즘의 처리 시간과의 상관관계입니다.
시간복잡도의 표현방법으로는
- Big O 표기법
: 알고리즘 실행시간의 상한을 나타낸 표기법 - Ω 표기법
: 알고리즘 실행시간의 하한을 나타낸 표기법 - Θ 표기법
: 알고리즘 실행시간의 평균시간을 나타낸 표기법
이제 간단한 코드를 보며 시간복잡도를 계산해보도록 하겠습니다.
int func2(int a[], int size, int key) {
int i = 0;
for(i=0 ; i<size ; i++)
if (a[i] == key)
return i;
return -1;
}코드를 보면 간단히 배열을 받고 size, 키를 받아서 배열을 사이즈만큼 포문을 돌려서 키값이랑 동일한지 체크하는 함수입니다. 이때 시간 복잡도를 계산할려면 실행횟수를 알면됩니다.
처음엔 i를 초기화해주는 줄은 1번
for문은 마지막에 조건문을 검사하기때문에 size + 1번
그 안에 있는 if문은 size번
그리고 if문을 만족하면 return문을 실행하니까 1번
만약 if문을 만족하지않는다면 -1을 return 해주므로 1번
이렇게 모든 실행횟수를 더해주면 2size + 4가 됩니다. 이걸 Big O 표기법으로 표시해봅시다. 아까 Big O 표기법의 규칙으로
계수 및 상수는 과감하게 버린다
라고했습니다. 이 규칙을 적용하게 된다면 최종적으론
size만 남음으로 O(n)으로 표기가 됩니다.
🏢 공간 복잡도
공간복잡도란 시간복잡도와 마찬가지로 비슷하지만 처리 시간 대신 메모리 사용량의 변화를 비교합니다. 최근에는 대용량 시스템이 보편화되면서 공간 복잡도보다는 시간 복잡도가 우선시됩니다.
공간 복잡도를 계산하는 방법은 실제 사용되는 저장공간을 계산하면 됩니다.
아래 코드를 보며 공간복잡도 계산을 해봅시다

반복문으로 팩토리얼을 구하는 간단한 코드입니다. 여기서의 공간복잡도는 반복문이 매개변수 n의 값에 상관없이 언제나 일정합니다. 때문에 Big O 표기법으로 구해보면
공간복잡도는 O(1)이 됩니다.
또 하나 예제를 봅시다

두 개의 코드가 무엇이 다른지 눈에 보이시나요? 바로 구현하는 방법이 다릅니다. 첫번째 코드는 반복문으로, 두번째코드는 재귀함수를 이용하였습니다.
재귀함수를 이용한 팩토리얼 구하기에선 n이 1이하일 때까지 함수가 재귀적으로 호출되면서 n부터 1까지 스택에 쌓이니까 입력 데이터의 크기에 비례하기 때문에 Big O 표기법으론 O(n)이 될 수 있습니다.
결론적으로
시간복잡도는 얼마나 빠르게 실행되느냐?
공간복잡도는 얼마나 많은 자원이 필요함?
좋은 알고리즘은 시간도 적게 걸리고 자원의 사용도 적어야하는 것이기 때문에 시간복잡도와 공간복잡도를 잘 고려해서 최적의 알고리즘을 짤 수 있습니다.
===출처 표기 예정
