Algorithm : Backtracking

1. Intro

• Tree 방문 순서의 종류
  
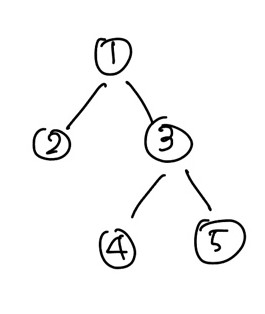
  위의 그림의 경우 순서 나열
  • preorder
    • 자신->왼쪽->오른쪽
    • 1->2->3->4->5
  • inorder
    • 왼쪽->자신->오른쪽
    • 2->1->4->3->5
  • post order
    • 왼쪽->오른쪽->자신
    • 2->4->5->3->1
  • level order
    • 깊이 순서로 방문
    • 1->2->3->4->5

2. Depth-First Search

• 깊이 우선 검색
  • root가 되는 노드 방문 후 후손 노드를 왼쪽에서 오른쪽으로 방문한다.
  • preorder 순서
• pseudo code

void dfs(node v)
{
 node u;
    
   visit v; //자신 방문
   for (each child u of v)
   	dfs(u);
}

3. 4-Queens problem

무작정 알고리즘

• 4x4 의 판으로 구성된 경우 $4^4 = 256$ 가지의 경우를 따져야함

상태공간트리

• root 부터 leaf까지 모두 탐색 해야하기 때문에 비효율적이다.

되추적(backtracking)

• 특정 노드를 확인하여 유망한지(promising) 아닌지를 판별하여 더 이상 후손 노드를 탐색하지 않도록 하여 효율성을 높여주는 방식
• 유망하지 않은 노드들은 pruning 하기 / 유망한 노드만 자손을 검색하기

void checknode (node v)
{
	node u;
    
    if(promising(v)) // 노드가 유망하면
    	if (there is a solution at v)
        	write the solution;
        else		// 노드가 유망하지 않으면
        	for (each child u of v)
            	checknode(u);
}

dfs VS. backtracking

• dfs : 155개의 노드 검색
• backtracking : 27개의 노드 검색
• pseudo code
  • 위의 코드는 방문한 후 유망한지 확인하는 것
  • 아래의 코드는 방문하기 전 유망한지 확인하는 것 (더 효율적)

void expand (node v)
{
	node u;
    
    for (each child u of v)
    	if (promising(u))
        	if(there is a solution at u)
            	write the solution;
            else
            	expand(u);
}

4. n-Queen problem

void queens(index i)
{
	if(promising(i))
    	if(i==n)
        	cout<<col[1] through col[n];
        else
        	for(j=1; j<=n; ++j)
            {
            	col[i+1] = j;
                queens(i+1);
            }
}

bool promising(index i)
{
	k=1;
    switch = true;
    while(k<i && switch)
    {	
    	if(col[i]==col[k] || abs(col[i]-col[k]) == i-k)
        	switch = false;
        k++;
    }
    return switch;
}

• 유망한지 여부 파악
  • col[i] == col[k] : 같은 column인지 확인
  • abs(col[i]-col[k]) == i-k) : 같은 대각에 있는지 확인
• 문제의 분석
  • 유망한 마디의 개수를 정확하게 구하기 위한 방법은 상태공간트리의 갯수를 직접 세어보는 방법밖에 없다.
  • but 이 방법은 알고리즘을 실행해야 알 수 있는 분석방법이기에 진정한 분석방법이 아니다.

5. 부분집합의 합 구하기

• n 개의 item을 가지고 무게의 합이 W가 되는 부분집합을 찾는 문제
• 무게가 증가하는 순서로 데이터를 정렬하면 유망한지 아닌지를 빠르게 판단할 수 있다.
• notation
  • $weight$ : 수준 i의 마디까지 포함된 무게의 합
  • $total$ : 남아있는 아이템의 무게의 총 합
  • 유망하지 않은 경우
    • $weight + w_{i+1} > W \\ or \\ weight+total<W$

void sum_of_subsets(index i, int weight, int total)
{
	if(promising(i))
    	if(weight == W)
        	cout<<include[1] through include[i];
        else
        {
        	include[i+1] = "yes";
            sum_of_subsets(i+1, weight + w[i+1], total-w[i+1]); //w[i+1] 포함
            include[i+1] = "no";
         	sum_of_subsets(i+1, weight , total-w[i+1]); //w[i+1] 불포함
        }
}

bool promising(index i)
	return (weight+total >= W && (weight == W||weight + w[i+1] <=W);

6. 그래프 색칠하기 (graph coloring)

Intro

• 인접하는 지역의 경우 다른 색으로 칠하는 문제
• 연결되는 그래프의 경우 다른 색으로 칠하는 문제

평면 그래프 (planer graph)

• 평면 상에서 edge가 교차되지 않고 그리는 방법

되추적 기법

• pseudo code
• 중요 부분
  • if(W[i][j] && vcolor[i] == vcolor[j])
  • 연결되어 있으면서 같은 색깔인지 확인하는 코드

void m_coloring(index i)
{
	if(promising(i))
    	if(i==n)
        	cout<<vcolor[1] through vcolor[n];
        else
        	for(color =1; color<=n; color++)
            {
            	vcolor[i+1] = color;
                m_coloring(i+1);
            }
}

bool promising(index i)
{
	switch = true;
    j=1;
    while(j<i && switch)
    {
    	if(W[i][j] && vcolor[i] == vcolor[j]) 
        	switch = false;
        j++;
    }
    return switch;
}