Algorithm : 계산 복잡도 (정렬 문제)

행렬 곱셈 문제

• 여러 시간 복잡도 분석..
  • 일반 알고리즘 $\Theta(n^3)$
  • Strassen 알고리즘 $\Theta(n^{2.81})$
  • Coppersmith/Winograd 알고리즘 $\Theta(n^{2.38})$
• Stability
  • 같은 키값을 갖는 데이터간의 정렬 전 순서가 정렬 후에도 유지되는 성질
  • 예시
    • Stable : insertion, merge, bubble
    • Not Stable : quick, heap, selection, exchange

삽입 정렬 알고리즘

void insertionsort(int n, keytype S[])
{
	for(int i = 2; i<=n; ++i)
    {
    	x = S[i];
        j = i-1;
        while(j > 0 && S[j] > x)
        {
        	S[j+1] = S[j];
            j--;
        }
        S[j+1] = x;
    }
}

• 비교하는 횟수를 기준으로 복잡도 분석
  • 최악의 경우
    • while 문 안에서 최대 i-1번의 비교
    • $W(n) = \frac{n(n-1)}{2}$
  • 평균의 경우
    • $A(n) = \frac{n^2}{4}$
• 공간 복잡도 분석
  • In-place sorting algorithm
  • 저장공간 따로 필요 없음 : $\Theta(1)$
• 레코드의 지정 횟수를 기준으로 복잡도 분석
  • 최악의 경우 : $W(n) = \frac{n^2}{2}$
  • 평균의 경우 : $A(n) = \frac{n^2}{4}$
• 비교 횟수나 레코드 지정 횟수 둘 중 아무거나 선택해도, 결과는 같음

선택 정렬 알고리즘

• 기준이 되는 데이터(i 인덱스)와 나머지 데이터 중 가장 작은 것 비교해서 바꾸기

void selectionsort(int n, keytype S[])
{
	for(int i=1; i<=n-1; ++i)
    {
    	smallest = i;
        for(int j=i+1; j<=n; ++j)
        {
        	if(S[j] < S[smallest])
            	smallest = j;
        }
        exchange S[i] and S[smallest];
    }
}

• 비교하는 횟수를 기준으로 복잡도 분석
  • $T(n) = \frac{n(n-1)}{2}$
• 공간 복잡도 분석
  • In-place sorting algorithm
  • 저장공간 따로 필요 없음 : $\Theta(1)$
• 레코드의 지정 횟수를 기준으로 복잡도 분석
  • $T(n) = 3(n-1)$

교환 정렬 알고리즘

• 기준이 되는 데이터(i)를 앞에서부터 하나씩 비교하면서 자기보다 작은 것 있으면 자신과 바꾸기

void exchangesort(int n, keytype S[])
{
	for(int i=1; i<=n-1; ++i)
    {
    	for(int j=i+1; j<=n; ++j)
        {
        	if(S[j] < S[i])
            	exchange S[i] and S[j];
        }
    }
}

• 비교하는 횟수를 기준으로 복잡도 분석
  • $T(n) = \frac{n^2}{2}$
• 레코드의 지정 횟수를 기준으로 복잡도 분석
  • 최악 : $W(n) = \frac{3n^2}{2}$ -> 모든 경우에 exchange 발생
  • 평균 : $A(n) = \frac{3n^2}{4}$ -> 비교하는 경우 절반에서 exchange 발생

거품 정렬 알고리즘

void bubblesort(int n, keytype S[])
{
	for(int i=n; i>=1; --i)
    {
    	for(int j=2; j<=i; ++j)
        {
        	if(S[j-1] > S[j])
            	exchange S[j-1] and S[j];
        }
    }
}

• 비교하는 횟수를 기준으로 복잡도 분석
  • $W(n)=A(n)=\frac{n(n-1)}{2}$
• 레코드의 지정 횟수를 기준으로 복잡도 분석
  • $W(n)=\frac{3n(n-1)}{2}$
  • $A(n)=\frac{3n(n-1)}{4}$

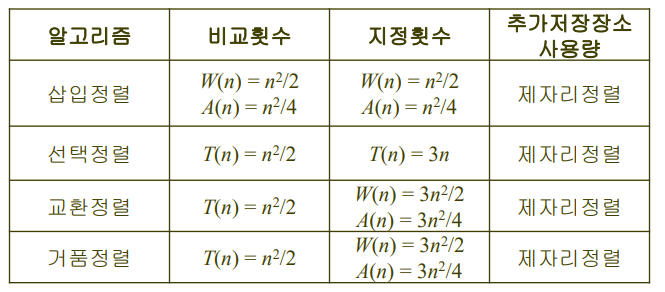
정리

한 번 비교하는데 최대한 하나의 역을 제거하는 알고리즘의 하한선

• 최악의 경우 $\frac{n(n-1)}{2}$ 번의 비교, 평균적으로 $\frac{n(n-1)}{4}$ 번의 비교 를 수행해야 한다.
• 증명
  • 최악의 경우 n개의 데이터가 있다면 $\frac{n(n-1)}{2}$개의 역을 가진다.
  • 한번의 하나의 역을 제거하므로 비교 횟수는 $\frac{n(n-1)}{2}$
  • 평균의 경우도 마찬가지 이다.

합병정렬 알고리즘 재검토

• 비교마다 하나 이상의 역을 제거하는 알고리즘
  • 교환, 삽입, 선택 정렬보다 효율적임

퀵 정렬 알고리즘

void quicksort(index low, index high)
{
	if(high>low)
    {
    	partition(low, high, pivotpoint);
        quicksort(low, pivotpoint-1);
        quicksort(pivotpoint+1, high);
    }
}

• 추가 공간이 필요함! $\Theta(lg \ n)$
  • 재귀로 인한 인덱스를 저장하기 위함

이진 트리

• 완전 이진 트리
• 실질적인 완전이진 트리
  • 깊이 d-1 까지는 완전 이진 트리이고 깊이 d는 왼쪽 끝부터 채워진 트리
• full binary tree

힙

Intro

• 부모 노드의 값은 자식 노드의 값보다 크거나 같다.
• 최대값 확인 $O(1)$
• 최대값 제거 및 재구성 $O(lg\ n)$
• 데이터 추가, 삭제, 변경 $O(lg\ n)$

Siftdown

• 교체하는 child node를 결정하기 위해 2회의 비교 필요

Siftup

• 자신의 부모와 1번의 비교만 한다.

힙정렬

• 순서
  • n개의 키를 이용하여 힙을 구성
  • 루트에 있는 제일 큰 값 제거
  • 힙 재구성
• make heap 방식
  • 데이터가 입력되는 순서대로 heap 구성
    • 최악의 경우 시간 복잡도 분석 (sift-up 분석)
      • $S=\sum_{j=0}^{d-1}j2^j$ -> $nlg\ n-2n+2$
      • $O(nlg\ n)$
  • 모든 데이터를 트리에 넣고 heap 구성
    • 최악의 경우 시간 복잡도 분석 (sift-down 분석)
      • $S=\sum_{j=0}^{d-1}2^j(d-j-1)$ -> $n-lg\ n-1$
      • $O(n)$
• 공간 복잡도
  • heap을 배열로 구현한 경우 $\Theta(1)$
• 시간 복잡도
  • Remove keys 분석
    • sift down 횟수 : $nlg\ n-2n+2$
    • 한번의 sift down에 있어서 두 번 비교
      • 총 비교 횟수 : $2nlg\ n-4n+4$
      • $\Theta(2nlg\ n)$

비교

결론

• 키 값의 비교를 통한 정렬은 $\Omega(nlg\ n)$의 복잡도를 갖는다.

기수 정렬

내용

• 분배에 의한 정렬 / 키에 대해서 아무런 정보가 없는 경우
• 왼쪽에서 오른쪽 자리순으로
  • 정수의 왼쪽부터 비교해서 1인것 2인것 3인것 ... 따로 분류하는 과정을 반복하기
• 오른쪽에서 왼쪽 자리순으로
  • 0~9 까지의 공간을 미리 만들어두고 넣으면되기 때문에 왼쪽에서 오른쪽 자리순으로 가는 방식보다 좋음

분석

• 뭉치에 수를 추가하는 연산을 단위 연산으로
  • 시간 복잡도
    • $T(n) = numdigits*(n+k)\in \Theta(numdigits*n)$
    • n은 정렬할 데이터 수, k는 각 자리의 범위(10 진수라면 10)
  • 공간 복잡도
    • $\Theta(n)$

Topological 정렬

• i에서 j로 가는 arc가 있을 때 i가 j 보다 먼저 오게 하는 정렬 방법
• 방문한지 안한지 체크하고, 방문하지 않았으면 dfs로 진행

void dfs(vertex v)
{
	stack S
    push(v,S)
    mark[v] = visited
    for each vertex w on L[v] do  //L[v] : v의 이웃 노드
    	if mark[w] = unvisited then
        	dfs(w)
   	print Top(S)
    Pop(S)
}