안녕하세요! 사설쓰는게 참 재밌는 GCOCO입니다!

유용한 정보를 제공하여 멋진 기술블로그가 되는것과는 거리가 멀게, 본인의 사설을 쓰는것을 더 즐기고 있는 기분이 듭니다!😀😅

다른 훌륭하신 분들은 아주 깔끔하게 관련 정보만을 기재해주시는 반면 제 포스팅을 보시면 아시다싶이
처음엔 항상 잡설로 시작한단말이죠~ 일기장에 가까워져 가는것 같습니다.

그럼에도 불구하고 잡설은 계속 쓸 것 같습니다!

대신 파트를 분리하여 바로 본론만 확인하실 수 있게끔 나누도록 하겠습니다.

---

잡설 한 COOKIE🍪

최근 중간고사를 마쳤다고 말씀드렸는데요, 이 정도로 제가 CPP에 허접❤ 할 줄은 몰랐습니다!
원하는 목표의 점수에 도달하지 못했고, 개념적으로 부족한 부분들도 많다고 느꼈던 중간고사였습니다.
하지만 나 GCOCO, CPP를 이용하여 무언가를 하여! 먹고 살자고 결정했기에!
당연히 실력을 보완해야 한다고 생각합니다!

따라서 개념을 정리한 포스팅들도 올리려고 합니다.
학교에서 사용하는 강의 자료를 소화하고 제가 깨우친 것들을 정리하여 올리도록 하겠습니다.

그럼, 오늘의 본론 시작하겠습니다!

---

BFS(Breadth-First Search)의 개념

너비 우선 탐색(BFS)는 그래프의 모든 정점을 너비 우선 순서로 탐색하는 그래프 순회 알고리즘입니다. 이것은 다음 레벨로 이동하기 전에 같은 레벨에 있는 모든 정점을 방문한다는 것을 의미합니다.

BFS를 구현하기 위해선 정점에서 시작하여 해당 정점에 인접한 모든 정점을 방문하여 방문한 것으로 표시합니다. 그런 다음 방문한 정점에 인접한 모든 정점을 방문하여 방문한 정점으로도 표시합니다. 그래프의 모든 정점이 방문될 때까지 이 과정을 반복합니다. 이것을 단계적으로 적어본다면, 다음과 같습니다!

1. 소스가 될 자료와, 방문 여부를 표시할 bool visited 배열을 준비한다.
2. 방문할 정점의 순서를 저장하기 위해 queue를 준비한다.
3. 소스 정점을 선택하고 방문한 것으로 표시하고 그런 다음 queue에 추가한다.
4. 큐가 비어 있지 않은 동안 큐의 앞쪽에서 방문해야 할 점을 빼서 방문하고 방문하지 않은 인접한 각 정점에 대해 방문한 것으로 표시하고 대기열의 뒤에 추가한다.
5. 대기열이 비워질 때까지 반복한다.

흠... 글로만 보면 헷갈리실것 같습니다. 역시! 그림으로 한번 보겠습니다.

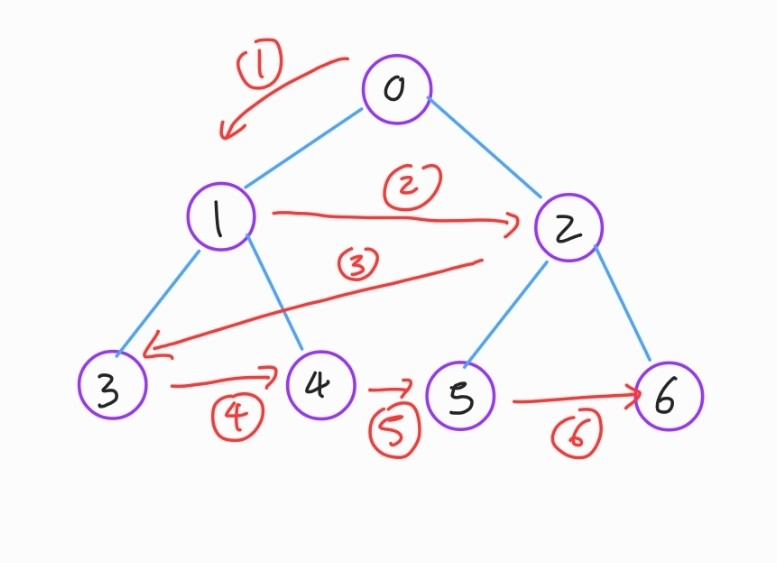
위 그림과 같은 노드 구조가 있고, 방문시 표시를 해주며, 왼쪽부터 방문한다고 가정한다면
어떻게 저런 순서가 되는걸까요?
아마 다음과 같은 형태로 queue에 담기고, 나갈것입니다.

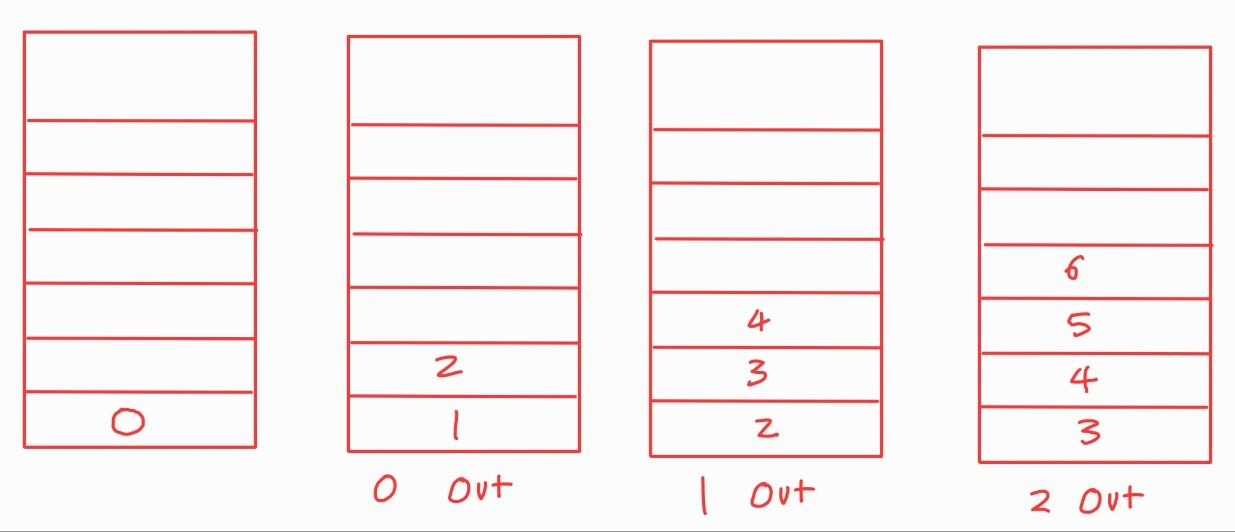
queue의 사이즈는 노드의 갯수만큼으로 설정해주었습니다!

1. 우선 정점인 0번 노드를 queue에 집어넣습니다.
2. 0번 노드를 빼내주고 0의 인접 노드인 1번 노드와 2번 노드를 queue에 순서대로 집어 넣어줍니다.
3. 1번 노드를 빼내주고 1의 인접 노드인 3,4번 노드를 queue에 넣어줍니다.
4. 2번 노드를 빼내주고 2의 인접 노드인 5,6번 노드를 queue에 넣어줍니다.
5. 3번 노드를 빼내주고 3은 인접 노드가 없기에 enqueue의 과정은 없습니다.
6. queue에 담긴 나머지 노드들은 3번 노드와 마찬가지 상황이므로, queue가 빌때까지 작업을 실시합니다.

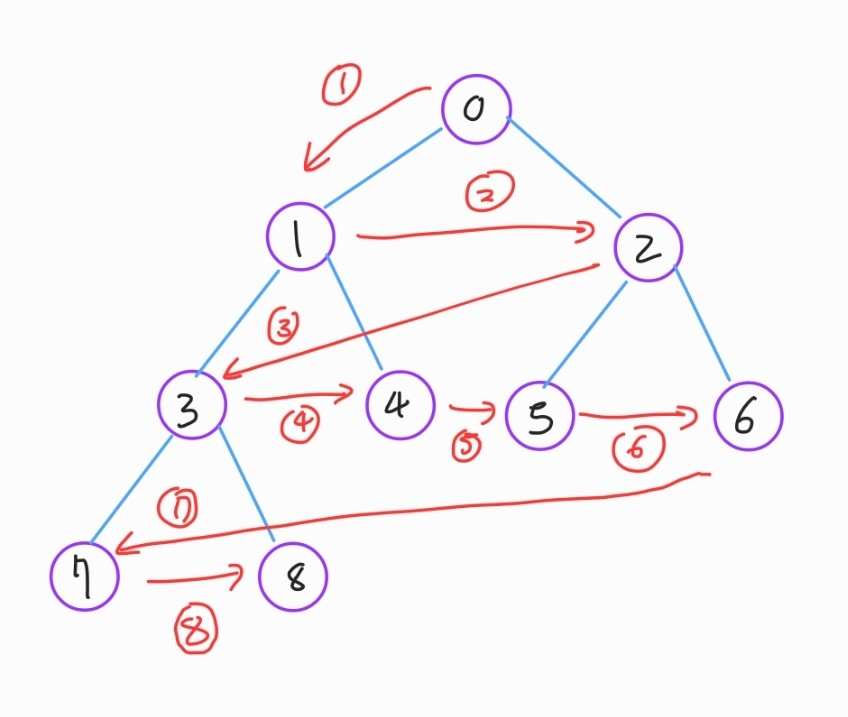
위의 그림 또한 비슷하게 예상하실수 있을것이라고 생각합니다!
이번엔 조금 다른 그림으로 볼까요?

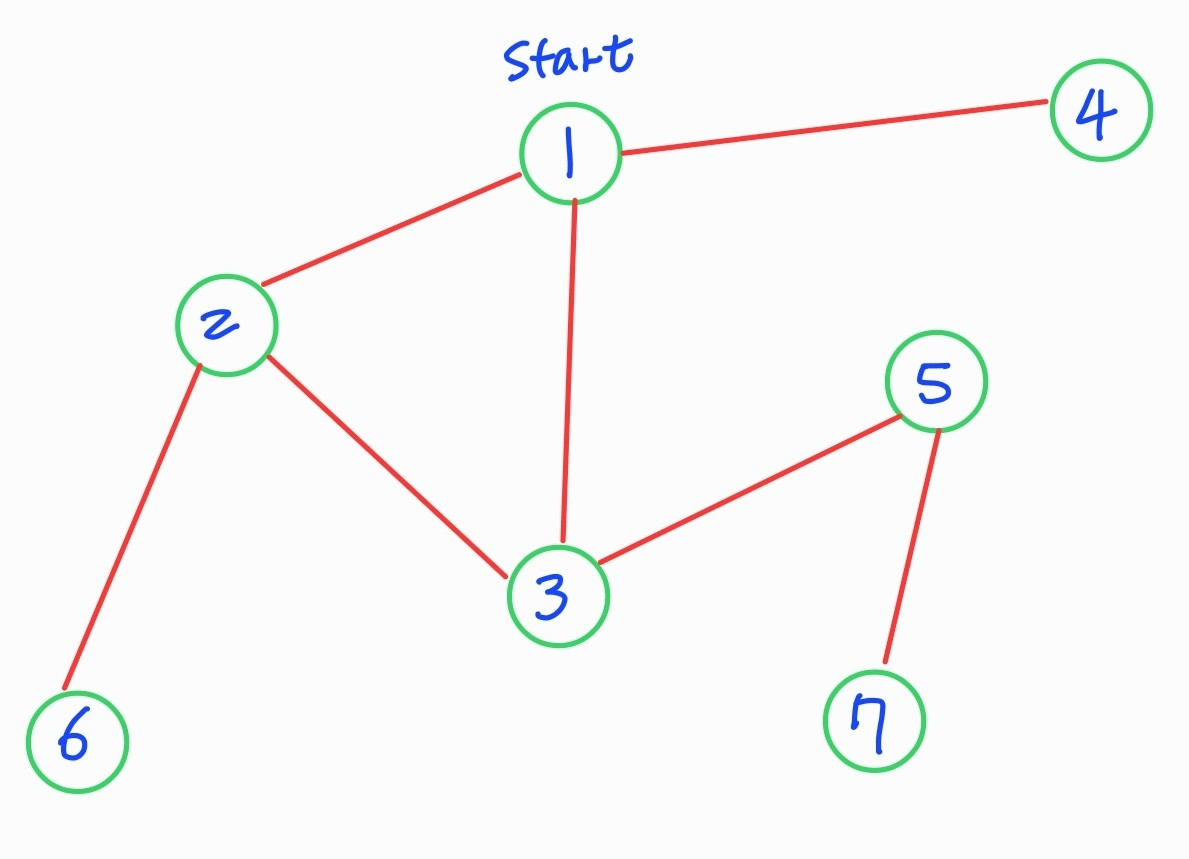
차근차근 생각해보도록 하겠습니다!
queue에 정점 1번이 담긴 상태이고, queue가 빌때까지 실행한다라고 가정하겠습니다.

1. 1을 빼내주고, 1의 인접 노드인 2,3,4,를 방문표시를 하고, queue에 담아줍니다.
2. queue의 front인 2번 노드를 빼내주고, 2번노드의 인접한 노드는 3번,6번 노드가 있으며 3번노드는 이미 방문하였기에, 6번노드를 queue에 담아줍니다.
3. queue의 front인 3번 노드를 빼내주고, 3번노드의 인접한 노드는 1번,2번,5번 노드가 있으며 1,2번 노드는 이미 방문하였기에, 5번 노드를 queue에 담아줍니다.
4. queue의 front인 4번 노드를 빼내주고, 4번 노드의 인접 노드는 없습니다.
5. queue의 front인 6번 노드를 빼내주고, 6번 노드의 인접 노드는 없습니다.
6. queue의 front인 5번 노드를 빼내주고, 5번 노드의 인접한 노드는 3번,7번 노드가 있으며 3번 노드는 이미 방문하였기에, 7번 노드를 queue에 담아줍니다.
7. queue의 front인 7번 노드를 빼내주고, 7번 노드의 인접 노드는 없습니다.
8. queue가 비었으므로, 탐색을 종료합니다.

즉 queue에 담긴 순서는 1 -> 2 -> 3 -> 4 -> 6 -> 5 -> 7이 됨을 알 수 있습니다!

---

위의 그림을 코드로 한번 짜 봅시다!

#include <iostream>
#include <string>
#include <vector>
#include <queue>

using namespace std;
void BFS(vector<vector<int>> source) {
    
    int n;
    n = source.size();
    //노드 방문 표시를 위한 visited 생성
    vector<bool> visited(n+1,false);
    //q를 이용하여 구현
    queue<int> q;
    //시작 정점 설정
    int start = 1;
    //시작점 방문 표시
    visited[start] = true;
    // 큐에 시작점 삽입
    q.push(start);
    cout << start << ' ';
    while (!q.empty()) {
        //현재 방문해야할 지점
        int now = q.front();
        //현재 방문점 방출
        q.pop();
        //현재 노드에 이어져있는 노드들 방문
        for (auto i : source[now]) {
            //방문하지 않은 노드라면
            if (!visited[i]) {
                //방문 표기 하고
                visited[i] = true;
                //큐에 삽입
                q.push(i);
                //탐색 순서를 확인하기 위한 출력
                cout << i << ' ';
            }
        }
    }

}

int main() {
    //그래프 생성, 직관적으로 볼 수 있게 1번부터 시작
    //각 노드들의 이어져있는 노드들을 담은 정보
    vector<vector<int>> graph = { {}, {2,3,4},{1,3,6},{1,2,5},{1},{3,7},{2},{5} };
    //BFS 호출
    BFS(graph);
    return 0;
}

위에 작성한 step에 따라 코드를 작성한다면, 이런 느낌의 코드가 되겠네요!
위 코드에선 직관적으로 매칭이 되게끔, 0번에 대한 정보를 기입한 graph를 사용하였습니다.

---

BFS, 그럼 어디다 써야하고 장점과 단점은 뭘까?

HEY GPT GOD, ANSWER ME.

장점은 다음과 같습니다.

1. 최단 경로 찾기 보장: BFS는 항상 시작 정점에서 거리 순서로 정점을 탐색합니다. 즉, 시작 정점과 그래프의 다른 정점 사이에서 항상 최단 경로를 찾습니다.

2. 완료: BFS는 완전한 알고리즘입니다. 즉, 결국 그래프에서 도달할 수 있는 모든 정점을 방문하게 됩니다.

3. 구현하기 쉬움: BFS는 구현하고 이해하기 쉬운 간단한 알고리즘입니다. 탐색할 정점을 추적하기 위한 대기열 데이터 구조만 필요합니다.

4. 다양한 그래프 문제를 해결하는 데 사용할 수 있습니다. BFS는 연결된 구성 요소 찾기, 주기 감지 및 이분성 확인과 같은 문제를 해결하는 데 사용할 수 있습니다.

단점은 다음과 같습니다.

1. 공간 복잡성: BFS는 모든 정점을 대기열에 저장해야 하므로 큰 그래프의 경우 문제가 될 수 있습니다. BFS의 공간 복잡도는 O(V)이며, 여기서 V는 그래프의 정점 수입니다.

2. 시간 복잡도: BFS의 시간 복잡도는 O(V+E)이며, 여기서 V는 정점의 수이고 E는 그래프의 엣지의 수입니다. 이는 간선이 많은 큰 그래프에서 문제가 될 수 있습니다.

3. 최장 경로 찾기에 적합하지 않음: BFS는 그래프에서 최단 경로를 찾도록 설계되었습니다. 즉, 두 정점 사이의 최장 경로를 찾는 데 적합하지 않습니다.

4. 주기에 갇힐 수 있음: BFS가 그래프에서 주기를 만나면 같은 꼭지점을 반복해서 탐색하는 데 정체되어 무한 루프로 이어질 수 있습니다. 이를 피하는 한 가지 방법은 방문한 정점을 표시하고 다시 탐색하지 않는 것입니다.

역시 깔끔하게 정리해주었습니다. 역시 G신.

장점에서 눈 여겨볼점은 최단경로 찾기, 구현하기 쉬움 인것같습니다.
실제로 제가 작성한 예시의 코드는 알기 쉽습니다.

단점에서 눈 여겨볼 점은 최장 경로 찾기에 적합하지 않다는 것과, 주기에 갇힐수 있다는 점입니다.
실제로 visited vector를 사용하지 않고 방문표기를 하지 않았다면, 계속해서 순환적 오류에 빠졌을것입니다.

---

BFS 관련 프로그래머스 문제를 이전의 포스팅에서 다뤘던 적이 있습니다.
코드만 가져와서 다시 간략하게 보도록 하겠습니다.

#include<vector>
#include <queue>
using namespace std;

int solution(vector<vector<int> > maps)
{
    int dx[4] = {-1,1,0,0};
    int dy[4] = {0,0,-1,1};
    
    int n = maps.size();
    int m = maps[0].size();
    
    queue<pair<int,int>> q;
    q.push(make_pair(0,0));
    
    vector<vector<int>> dist(n,vector<int>(m,-1));//거리를 저장할 vector
    dist[0][0] = 1;//시작점의 거리값을 1로 초기화
    while(!q.empty()){
    	//현재 지점의 x,y값 저장
        int x = q.front().first;
        int y = q.front().second;
        q.pop();
        
        for(int i=0;i<4;i++){
        	//상 하 좌 우 탐색
            int nx = x + dx[i];
            int ny = y + dy[i];
            //범위내의 값이라면 
            if(0<=nx && nx<n && 0<=ny && ny<m){
            	//갈 수 있는 지형이고, 아직 방문하지 않은 곳이라면
                if(maps[nx][ny] && dist[nx][ny]==-1){
                	//해당 지점까지의 거리 계산
                    dist[nx][ny] = dist[x][y]+1;
                    //해당 지점에서의 탐색을 위해 queue에 삽입
                    q.push(make_pair(nx,ny));
                }
            }
        }
    }
    //마지막 지점에서의 거리값 반환(도착하지 못할시 default값인 -1 반환)
    return dist[n-1][m-1];
}

BFS개념 부분에서 설명한 바와 같이 이 코드에선 q를 통해 queue의 역할을 수행하고, dx,dy를 이용해 상하좌우를 탐색하며, maps라는 갈 수 있는 길에 대한 정보와 dist라는 2차원 벡터를 이용해 방문여부를 확인하며 탐사를 진행하는것을 볼 수 있습니다!

---

마치며😁

이 글은 DFS와 함께 하나의 포스팅에 작성될 예정이었으나, 생각보다 한번에 보기에 양이 길어지는듯 하여 나눠서 포스팅 하게 되었습니다. 제 글이 아주 작은 도움이라도 되었기를 바라며, 마치겠습니다.

감사합니다!