이진트리: 모든 노드의 최대 차수를 2로 제한한 트리

완전 이진 트리: 이진트리에 아래 조건을 만족하는 트리

1. 마지막 레벨을 제외한 모든 노드가 채워져있어야함
2. 모든 노드들은 왼쪽부터 채워져있어야함

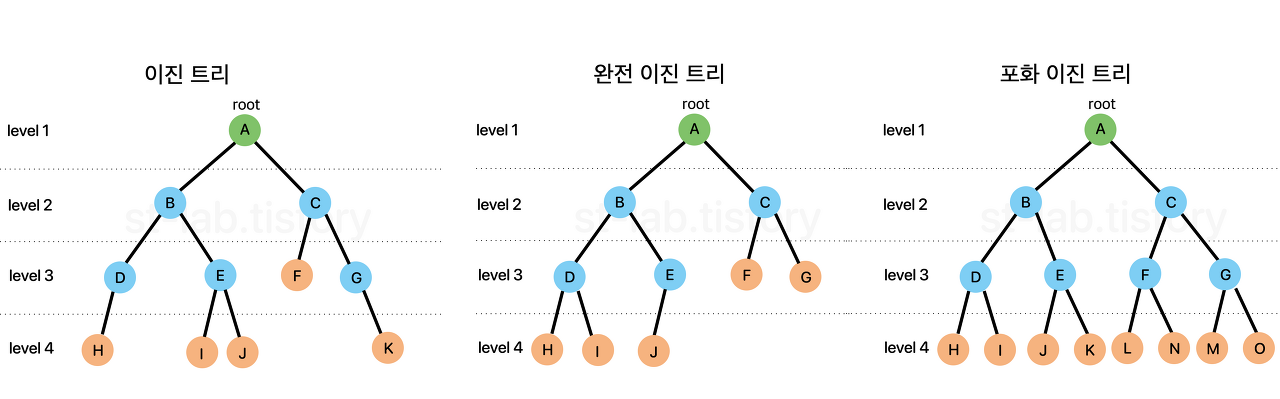
⇒ 이 구조를 활용해서 최대값/최소값을 빠르게 찾아내는 구조 = 힙

힙(heap)

정의

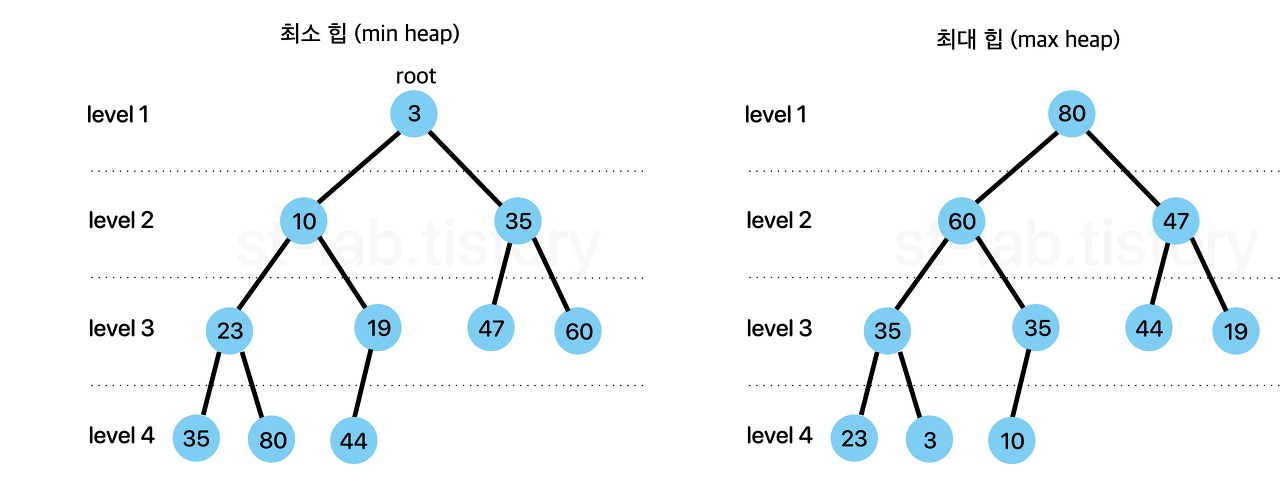
힙은 '최솟값 또는 최댓값을 빠르게 찾아내기 위해 완전이진트리 형태로 만들어진 자료구조'다.

= 부모 노드는 항상 자식 노드보다 우선순위가 높다는 조건을 만족시키면서 완전이진트리 형태로 채워나가는 것

이때, 형제 간 우선순위는 고려되지 않는다.

? 왜 형제 간에는 대소비교가 필요없을까?

우선순위가 높은 순서대로만 뽑으면 되기 때문에

시간복잡도

탐색에는 시간복잡도 : O(1)

삽입삭제: O(logN) *부모노드가 자식노드보다 우선순위만 높으면 되므로 결국 트리의 깊이만큼만 비교를 하면 되기 때문에

Primary Queue 사용해서 heap구현하는 방법

import java.util.PriorityQueue;

//오름차순(최소힙)
PriorityQueue<Integer> minheap = new PriorityQueue<>();

//내림차순(=최대힙) 
PriorityQueue<Integer> maxheap = new PriorityQueue<>(Collections.reverseOrder());

구현

⇒ 자바에서 힙은 배열로 구현한다. (LinkedList로 구현이 가능하지만, 특정 노드의 '검색', '이동' 과정이 조금 더 번거롭기 때문)

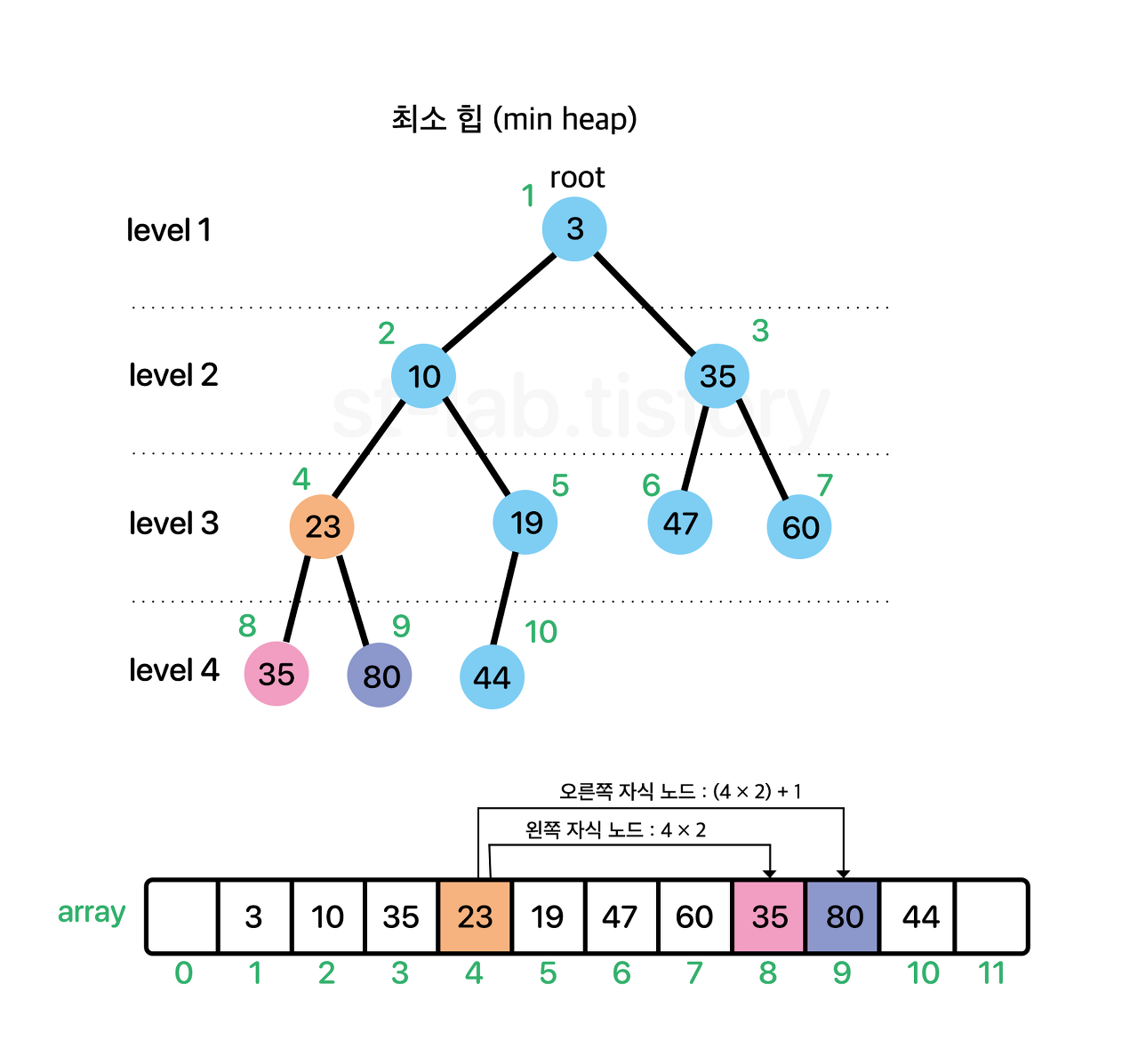
과정:

1. 구현의 용이함을 위해 시작 인덱스(root)는 1 부터 시작한다.
2. 각 노드와 대응되는 배열의 인덱스는 '불변한다'

그럼 다음과 같은 성질을 가지게 됨

1. 왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2
2. 오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2 + 1
3. 부모 노드 인덱스 = 자식 노드 인덱스 / 2

import java.util.Comparator;
 
public class Heap<E> {
 
	private final Comparator<? super E> comparator;
	private static final int DEFAULT_CAPACITY = 10;	// 최소(기본) 용적 크기 
    
	private int size;	// 요소 개수 
 
	private Object[] array;	// 요소를 담을 배열 
 
	// 생성자 Type 1 (초기 공간 할당 X)
	public Heap() {
		this(null);
	}
	
	public Heap(Comparator<? super E> comparator) {
		this.array = new Object[DEFAULT_CAPACITY];
		this.size = 0;
		this.comparator = comparator;
	}
    
	// 생성자 Type 2 (초기 공간 할당 O)
	public Heap(int capacity) {
		this(capacity, null);
	}
	
	public Heap(int capacity, Comparator<? super E> comparator) {
		this.array = new Object[capacity];
		this.size = 0;
		this.comparator = comparator;
	}
    
 
	// 받은 인덱스의 부모 노드 인덱스를 반환
	private int getParent(int index) {
		return index / 2;
	}
	
	// 받은 인덱스의 왼쪽 자식 노드 인덱스를 반환 
	private int getLeftChild(int index) {
		return index * 2;
	}
	
	// 받은 인덱스의 오른쪽 자식 노드 인덱스를 반환
	private int getRightChild(int index) {
		return index * 2 + 1;
	}
	
	
}