
선분 3개가 평행하게 놓여 있습니다. 세 선분의 시작과 끝 좌표가 [[start, end], [start, end], [start, end]] 형태로 들어있는 2차원 배열 lines가 매개변수로 주어질 때, 두 개 이상의 선분이 겹치는 부분의 길이를 return 하도록 solution 함수를 완성해보세요.
lines가 [[0, 2], [-3, -1], [-2, 1]]일 때 그림으로 나타내면 다음과 같습니다.
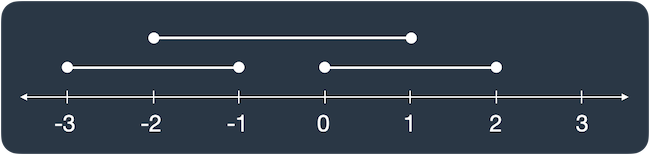
선분이 두 개 이상 겹친 곳은 [-2, -1], [0, 1]로 길이 2만큼 겹쳐있습니다.
제한사항
- lines의 길이 = 3
- lines의 원소의 길이 = 2
- 모든 선분은 길이가 1 이상입니다.
- lines의 원소는 [a, b] 형태이며, a, b는 각각 선분의 양 끝점 입니다.
- -100 ≤ a < b ≤ 100
입출력 예
| lines | result |
|---|---|
| [[0, 1], [2, 5], [3, 9]] | 2 |
| [[-1, 1], [1, 3], [3, 9]] | 0 |
| [[0, 5], [3, 9], [1, 10]] | 8 |
입출력 예 설명
입출력 예 #1
두 번째, 세 번째 선분 [2, 5], [3, 9]가 [3, 5] 구간에 겹쳐있으므로 2를 return 합니다.
입출력 예 #2
겹친 선분이 없으므로 0을 return 합니다.
입출력 예 #3
첫 번째와 두 번째 선분이 [3, 5] 구간에서 겹칩니다.
첫 번째와 세 번째 선분 [1, 5] 구간에서 겹칩니다.
두 번째와 세 번째 선분 [3, 9] 구간에서 겹칩니다.
따라서 [1, 9] 구간에 두 개 이상의 선분이 겹쳐있으므로, 8을 return 합니다.
나의 풀이
function solution(lines) {
const start = lines.map(v => v[0]);
const end = lines.map(v => v[1]);
let count = 0;
let intersection = 0;
for(let i = Math.min(...start); i <= Math.max(...end); i++){
for(let j = 0; j < lines.length; j++){
if(i >= start[j] && i < end[j]){
count++
}
}
if(count >= 2){
intersection++
}
count = 0;
}
return intersection
}2차원 배열의 앞쪽 값이 시작값, 뒤쪽 값이 종료값이기 때문에 시작값과 종료값을 각각 다른 배열로 분리시켜 주었다. 시작값의 최소값이 가장 작은 값, 종료값의 최대값이 가장 큰 값일 것이기 때문에 그 값들을 각각 검사해 주었다. 만일 그 값이 다른 선분과 비교했을 때 겹치는 값이라면 count값을 증가시켜 주었다. 이를 통해 각 점에서 선분이 겹치는 개수를 셀 수 있다. 최종적으로 count가 2이상이라면 intersection 값을 증가시켜 주었고, intersection 값을 return해 주었다.
가장 큰 고민은 depth가 3까지 늘어난다는 점이었다. 이렇게 for과 if를 중첩시키면 가독성이 너무 떨어져서 고민이 많이 되었는데, 이 방법으로는 중첩을 줄일 방법이 생각이 나질 않았다.
참고할 풀이
function solution(lines) {
let line = new Array(200).fill(0);
lines.forEach(([a, b]) => {
for(; a < b; a++) line[a+100]++;
});
return line.reduce((a, c) => c > 1 ? a + 1 : a, 0)
}이 풀이는 line이라는 0으로 채워진 새로운 배열을 만들어 준 다음, lines 범위에 해당한다면 값을 각각 1씩 증가시켜 주었다. line[a+100]의 값을 증가시켜준 이유는, lines에 음수의 값도 존재하기 때문이다. 그리고 reduce를 이용해서 값이 1보다 크다면 1을 더해 전체 겹치는 부분의 합을 계산해 주었다. reduce 이외에도 filter을 사용해서 풀 수도 있을 듯 하다. 직관적이고, 무엇보다도 depth 문제를 해결해준 풀이라 참고할 만하다.
