Graphics APIs

그래픽스 API로는 DirectX, OpenGL, Vulkan, Metal 등이 있다.
DirectX는 window 플랫폼 기반의 그래픽스 api이다.
DirectX 12와 11의 차이점은 DirectX 12는 저수준까지 다루는 api이고, 병렬처리를 지원한다.

기본 개념

Vectors

벡터는 크기와 방향을 갖는다.
DirectX는 left-handed coordinate system을 따른다.

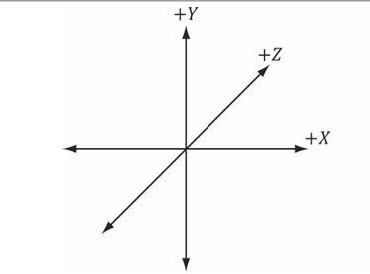
손을 X에서 Y로 감을 때 엄지의 방향이 Z

Basic Vector Operations

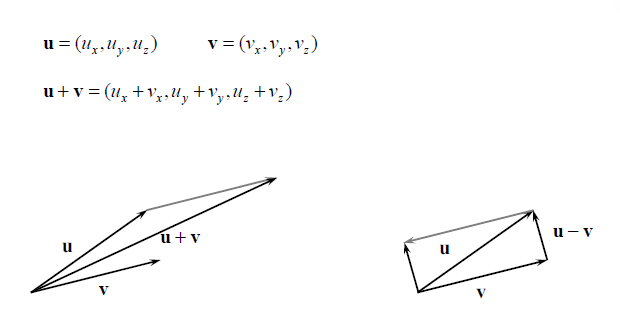
Length and Unit Vectors

unit vector(단위 벡터)는 크기가 1인 vector이다. ^ 기호를 사용한다.

---

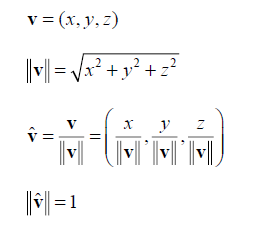
Dot Product

내적이 만들어내는 것은 한 벡터를 다른 벡터에 projection 시킨 후 둘을 곱한 값이다. 즉, 스칼라이다.

위에서 부터 하나씩 살펴보자.

먼저 맨 위는 내적의 정의이다.
$\overrightarrow{u} \cdot \overrightarrow{v} = ||u||*||v||*cos(\theta)$를 보면 $v$ 벡터를 $u$ 벡터에 proj 시킨다는 것을 알 수 있다.

두 벡터 사이의 각이 $\theta$이다.

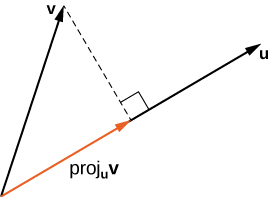
$cos(\theta)$의 값은 $\theta$가 0 ~ 180일 때 값이 1 ~ -1이므로 직각일 땐 내적이 0, 예각일 땐 양수, 둔각일 땐 음수임을 알 수 있다.

이제 세 번째를 살펴보자.
$v$벡터를 $\hat{n}$ 단위 벡터에 proj 시킨 벡터를 구하는 것이다.

마지막은 $v$벡터를 $n$에 proj 시키는 것인데 이는 $n$을 정규화하여 사용한다.

그 다음 $n$에 수직인 벡터를 만드는 것인데 이는 벡터의 뺄셈을 이용하여 $v-proj_uv$로 구할 수 있다.

Orthogonaliztion

직교화는 직교하지 않은 벡터들의 집합을 직교하는 벡터들의 집합으로 변환하는 것이다.

1. 먼저 집합의 첫 벡터를 $w_0$로 설정한다.

2. $w_1$부터 $w_{n-1}$까지 직교화한다.

3. 정규화 한다.

---

Cross Product

외적은 3차원 벡터에서만 정의한다.
외적이 만드는 것은 두 벡터가 만든 평면에 직교하는 벡터이다.

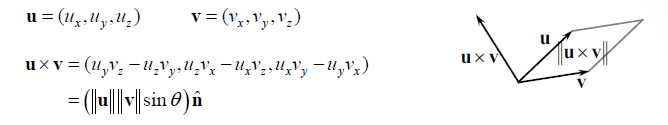
외적의 결과는 다음과 같이 해석한다. 두 벡터가 만든 평행사변형 곱하기 그 것의 직교하는 단위벡터 (직교하는 단위벡터는 왼손 법칙을 따른다)

외적으로 직교화 하는 방법

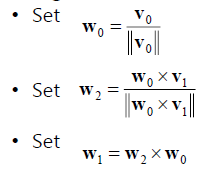
$sin(\theta)$의 연산을 통해 직교하는 벡터를 만들어낼 수 있으므로 외적으로도 직교화가 가능하다.

과정은 위의 그림과 같다.

---

DirectX 코드

XMVECTOR Type

XMVECTOR 혹은 XMMATRIX는 SIMD상 CPU에서 연산을 한다.

// XMVECTOR
#if defined(_XM_NO_INTRINSICS_)
    struct __vector4
    {
        union
        {
            float       vector4_f32[4];
            uint32_t    vector4_u32[4];
        };
    };
#endif // _XM_NO_INTRINSICS_

    //------------------------------------------------------------------------------
    // Vector intrinsic: Four 32 bit floating point components aligned on a 16 byte
    // boundary and mapped to hardware vector registers
#if defined(_XM_SSE_INTRINSICS_) && !defined(_XM_NO_INTRINSICS_)
    using XMVECTOR = __m128; // SSE
#elif defined(_XM_ARM_NEON_INTRINSICS_) && !defined(_XM_NO_INTRINSICS_)
    using XMVECTOR = float32x4_t; // for ARM SIMD
#else
    using XMVECTOR = __vector4; // XM_NO_INTRINGSICS_
#endif

위의 코드를 보면 회색으로 보이는 부분이 많다. 회색으로 보이는 부분은 전처리 문에 의해 컴파일 되지 않고 컴파일 전에 어떤 부분의 코드를 실행할지 결정된다!

즉, 이는 다양한 버전을 지원할 수 있는 것이다.

또한 XMVECTOR는 128비트 크기의 4개 float 값을 저장하는 구조이다. 그래서 Set 함수의 인자도 다음과 같다.

XMVECTOR XM_CALLCONV XMVectorSet(float x, float y, float z, float w) noexcept;

W?

여기서 W는 왜 필요한 것일까?
그래픽 프로그래밍에서는 벡터 연산이나 좌표 변환을 할 때 w 값이 중요한 역할을 한다.

• w = 1.0f이면 위치(Position) 벡터 (좌표 변환 시 사용)
• w = 0.0f이면 방향(Direction) 벡터 (단위 변환 없이 사용)

즉, 1.0f이면 좌표 변환 시 이동의 영향을 받고 0.0f이면 방향만 유지된다.

---

Calling conventions

함수 호출 규약(Calling Convention)이란, 함수를 호출하는 방식에 대한 약속이다.

예를 들어, directX의 XMVECTOR 호출 규약은 일반적인 C++ 구조체와 다르게 동작한다. 이는 성능 최적화를 위해 특별한 레지스터 패싱 방식을 따르기 때문이다.

XMVECTOR는 레지스터를 사용하지 않고 스택(stack)에 복사되어 전달된다. 이를 방지하고 성능 최적화를 위해 FXMVECTOR, CXMVECTOR 등의 대체 타입을 사용한다.

FXMVECTOR: 처음 3개의 XMVECTOR 인자로 사용
GXMVECTOR: 4번째 XMVECTOR의 인자
HXMVECTOR: 5, 6번째 XMVECTOR의 인자
CXMVECTOR: 이후 추가 XMVECTOR의 인자

XMVECTOR XM_CALLCONV XMLoadFloat3 (const XMFLOAT *pSource) noexcept;

여기서 XM_CALLCONV이 호출 규약을 지정하는 매크로이다.

• 참고로 noexcept 키워드는 이 함수가 절대로 예외를 던지지 않는다는 뜻이다.

---

struct XMFLOAT3

XMFLOAT3는 GPU에서 연산을 한다.

XMFLOAT3는 3차원, floating point (부동소수점) 3개를 사용한다.

    struct XMFLOAT3
    {
        float x;
        float y;
        float z;

        XMFLOAT3() = default;

        XMFLOAT3(const XMFLOAT3&) = default;
        XMFLOAT3& operator=(const XMFLOAT3&) = default;

        XMFLOAT3(XMFLOAT3&&) = default;
        XMFLOAT3& operator=(XMFLOAT3&&) = default;

        constexpr XMFLOAT3(float _x, float _y, float _z) noexcept : x(_x), y(_y), z(_z) {}
        explicit XMFLOAT3(_In_reads_(3) const float* pArray) noexcept : x(pArray[0]), y(pArray[1]), z(pArray[2]) {}
    };

float형 변수 3개가 있음을 알 수 있다.

변환

다음 두 함수를 보자.

void XM_CALLCONV XMStoreFloat3 (XMFLOAT3 *pDestination, FXMVECTOR v) noexcept;

XMVECTOR XM_CALLCONV XMLoadFloat3 (const XMFLOAT *pSource) noexcept;

이 두 함수는 XMVECTOR와 XMFLOAT3 간의 변환을 위해 정의한 함수들이다.

먼저 첫 번째 함수는 FMVECTOR v의 값을 XMFLOAT3 구조체에 저장하는 역할을 한다. 변환된 값을 저장하기 위해 XMFLOAT3형 포인터를 정의하였다.

두 번째 함수는 XMFLOAT3 값을 XMVECTOR 타입으로 변환하여 반환한다.

참고로 함수 반환형 앞에있는 XM_CALLCONV는 calling convention이다.

---

예제

다음 예제의 실행 결과와 실제로 계산해보면 계산 값이 동일함을 알 수 있다.

int main()
{
    cout.setf(ios_base::boolalpha);

    // Check support for SSE2 (Pentium4, AMD K8, and above).
    if (!XMVerifyCPUSupport())
    {
        cout << "directx math not supported" << endl;
        return 0;
    }

    XMVECTOR n = XMVectorSet(1.0f, 0.0f, 0.0f, 0.0f); // XMVECTOR 4개 정의!
    XMVECTOR u = XMVectorSet(1.0f, 2.0f, 3.0f, 0.0f);
    XMVECTOR v = XMVectorSet(-2.0f, 1.0f, -3.0f, 0.0f);
    XMVECTOR w = XMVectorSet(0.707f, 0.707f, 0.0f, 0.0f);

    // Vector addition: XMVECTOR operator + 
    XMVECTOR a = u + v;

    // Vector subtraction: XMVECTOR operator - 
    XMVECTOR b = u - v;

    // Scalar multiplication: XMVECTOR operator * 
    XMVECTOR c = 10.0f*u;

    // ||u||
    XMVECTOR L = XMVector3Length(u);

    // d = u / ||u||
    XMVECTOR d = XMVector3Normalize(u);

    // s = u dot v
    XMVECTOR s = XMVector3Dot(u, v); // 내적의 결과는 scalar인데 벡터로 정의했다. 
    								 // 연산을 위해 벡터로 만든 것이다. 
                                     // 내적의 결과가 -9일때 결과 값 (-9, -9, -9)

    // e = u x v
    XMVECTOR e = XMVector3Cross(u, v);

    // Find proj_n(w) and perp_n(w)
    XMVECTOR projW;
    XMVECTOR perpW;
    XMVector3ComponentsFromNormal(&projW, &perpW, w, n);

    // Does projW + perpW == w?
    bool equal = XMVector3Equal(projW + perpW, w) != 0;
    bool notEqual = XMVector3NotEqual(projW + perpW, w) != 0;

    // The angle between projW and perpW should be 90 degrees.
    XMVECTOR angleVec = XMVector3AngleBetweenVectors(projW, perpW); // 사잇각 구하기
    float angleRadians = XMVectorGetX(angleVec);
    float angleDegrees = XMConvertToDegrees(angleRadians); // degree로 변환

    cout << "u                   = " << u << endl;
    cout << "v                   = " << v << endl;
    cout << "w                   = " << w << endl;
    cout << "n                   = " << n << endl;
    cout << "a = u + v           = " << a << endl;
    cout << "b = u - v           = " << b << endl;
    cout << "c = 10 * u          = " << c << endl;
    cout << "d = u / ||u||       = " << d << endl;
    cout << "e = u x v           = " << e << endl;
    cout << "L  = ||u||          = " << L << endl;
    cout << "s = u.v             = " << s << endl;
    cout << "projW               = " << projW << endl;
    cout << "perpW               = " << perpW << endl;
    cout << "projW + perpW == w  = " << equal << endl;
    cout << "projW + perpW != w  = " << notEqual << endl;
    cout << "angle               = " << angleDegrees << endl;

    return 0;
}

위 코드의 실행 결과는 아래와 같다.

u                   = (1, 2, 3)
v                   = (-2, 1, -3)
w                   = (0.707, 0.707, 0)
n                   = (1, 0, 0)
a = u + v           = (-1, 3, 0)
b = u - v           = (3, 1, 6)
c = 10 * u          = (10, 20, 30)
d = u / ||u||       = (0.267261, 0.534522, 0.801784)
e = u x v           = (-9, -3, 5)
L  = ||u||          = (3.74166, 3.74166, 3.74166)
s = u.v             = (-9, -9, -9)
projW               = (0.707, 0, 0)
perpW               = (0, 0.707, 0)
projW + perpW == w  = true
projW + perpW != w  = false
angle               = 90

위 코드에서 내적값이나 각도를 XMVECTOR로 지정한 것을 알 수 있는데 이는 연산을 위해 벡터로 만든 것이다.

내적값이 -9가 나왔다면 (-9, -9, -9)의 벡터를 만드는 것이다.