지난 장에 이어 이번엔 Tree & Binary Tree에 대해 알아봅니다.

개념을 익히고, pseudo code를 작성한 뒤, 실제 코드는 따로 수정합니다! ✍🏻

---

🌲 Tree

1. Tree

말그대로 나무처럼 가지를 뻗어나가는 형태입니다.

HTML구조에서 DOM 의 구조를 생각하시면 됩니다.

계층 구조로 된 다양한 곳에 사용됩니다!

노드의 종류는 간략하게 3가지로 나뉩니다.
1. 가장 최상단 노드인 루트 노드
2. 루트 노드에서 이어지는 자식 노드
3. 자식 노드가 없는 리프 노드

계층적 구조로 되어 있고, 루트노드에서 어떤 자식노드로 이어지는 길은 유일합니다.

노드와 노드 사이를 이어주는 가지를 branch 또는 edge 라고 합니다.

그 말은 즉, 각 자식 노드의 부모는 유일합니다.

트리를 구현할 때에는 앞서 배운 구조들과는 차이점이 있습니다. head, tail을 사용하지 않죠.

먼저 이진 트리의 사진을 참고하여 알아봅니다.

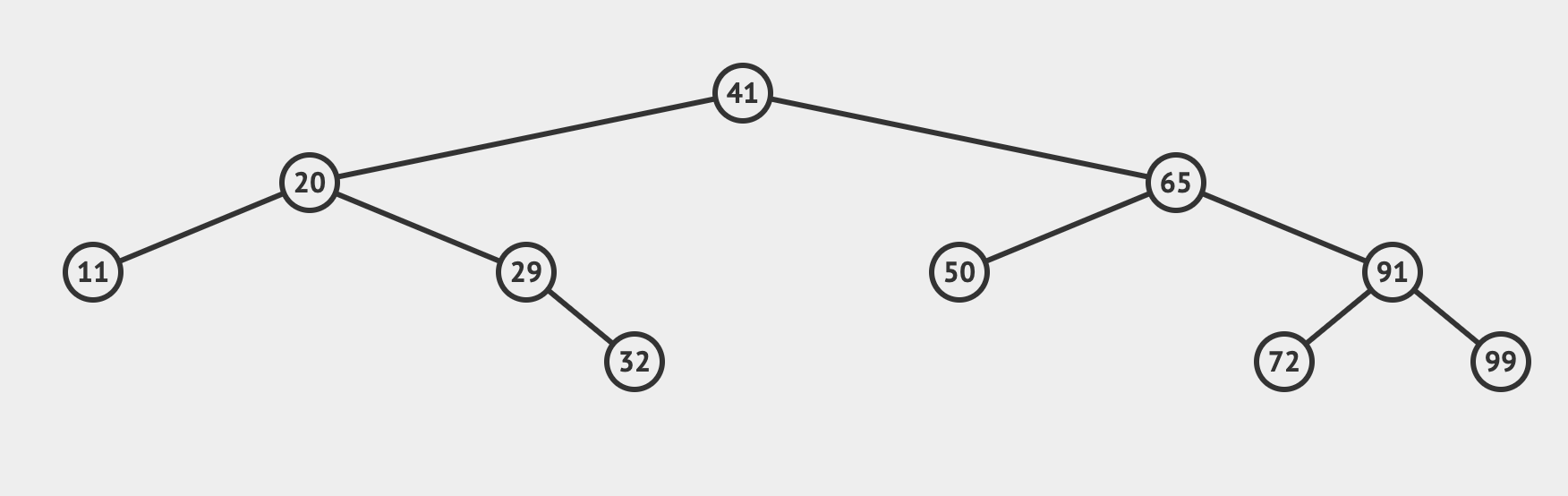
트리는 위 사진에서 자식의 개수에 제한이 없습니다. 한 노드에서 무한정으로 뻗어나갈 수 있죠.

트리의 공통적인 사항은 value가 유일하다는 점입니다. 중복될 수 없습니다.

그럼 포인트 2가지가 나왔네요. 이 2가지를 기억하고 코드를 구현해봅니다.

1. children의 개수에 제한이 없다.
2. 모든 value는 중복될 수 없다.

2. pseudo Code

간단한 pseudo Code로 작성해봅시다.

/* pseudo Code */
트리 {
 children, value 
  
 method: addChild(v) {
  children에 tree추가 
 }
 
 method: contains(v) {
   tree의 children을 순회
   v와 일치하면 true, 아니면 false
 }
}

3. Tree Code

트리의 code를 구현해봅시다.

이번엔 function shared 패턴을 사용하여 구현을 하였습니다.

treeMethods라는 객체에 메소드를 구현하여 _.extend로 newTree에 확장해줍니다.

_.extend(A, B)는 A객체에 B객체를 연장해서 추가한다고 생각하시면 됩니다.

각 구성을 간단히 분석해봅시다.

value : 말그대로 각 트리노드의 value값입니다.
children : 트리를 추가할 때마다 children배열에 넣어줍니다.
addChild : tree를 생성하여 children에 푸쉬합니다. 이 부분이 좀 헷갈렸습니다.
--------- 어떻게 children의 tree에 접근할지를 몰랐었는데요.
--------- 알고보니 직접 children에 접근하여 추가를 하고 있었습니다 😂
contains : goDeeper라는 재귀를 생성하여 children배열을 돌면서 체크합니다.

const _ = require('underscore')

const Tree = function(value) {
  const newTree = {};
  newTree.value = value;
  newTree.children = [];

  _.extend(newTree, treeMethods)
  return newTree;
};

const treeMethods = {};

treeMethods.addChild = function(value) {
  var tree = new Tree(value);
  tree.value = value;
  this.children.push(tree);
};

treeMethods.contains = function(target) {
  var isContain = false;

  const goDeeper = (children, target) => {
    for(let i = 0; i < children.length; i++) {
      if (target === children[i].value) {
        isContain = true
      } else {
        goDeeper(children[i].children, target)
      }
    }
  }

  goDeeper(this.children, target)
  return isContain
};

---

🌳 Binary Search Tree (BST)

1. Binary Tree (B-tree)

이진 트리는 각 노드의 자식 노드가 최대 2개인 트리입니다.

역시 그림이 편하겠죠? tree에서 사용했던 이진 트리를 가져와 봅니다.

위처럼 최상단 노드를 Root노드, 자식이 없는 노드를 leaf노드라고 합니다.

이진 트리는 탐색 속도를 빠르게 하는 용도로 사용하는데요.

Root에서 출발할 때, 왼쪽 또는 오른쪽을 선택하면 반대쪽을 아예 고려하지 않습니다.

즉, 한 칸씩 내려갈 때마다 탐색 횟수가 절반씩 감소하는 것이죠!

완전 이진 트리의 경우에는 리프노드를 제외한 모든 노드가 2개의 자식을 가집니다.

모든 노드를 배열에 담아 구현하면 되는 것이죠.

하지만 자유로운 이진 트리의 경우에는 그렇지 않으므로, 구현 방법이 다릅니다.

동일하게 구현할 경우, 자식이 없는 공간도 배열에 추가되어 낭비가 됩니다.

그래서, 노드의 개수만큼만 공간을 생성하여야 합니다.

2. B-Tree 순회

코드 작성 전에, 이진 트리의 3가지 순회 방식을 알아봅시다.

순회 방식은 자기 자신의 처리 순서에 따라 전위 / 중위 / 후위 3가지로 나뉩니다.
1. 전위 : 자기 자신 -> 왼쪽 자식 -> 오른쪽자식
2. 중위 : 왼쪽 자식 -> 자기 자신 -> 오른쪽 자식
3. 후위 : 왼쪽 자식 -> 오른쪽 자식 -> 자기 자신

3. Binary Search Tree

이진 탐색 트리의 조건은 다음과 같습니다.

1. 모든 value는 중복될 수 없다.
2. 각 노드의 최대 자식 개수는 2개이다. (tree는 개수 제한이 없음)
3. 왼쪽 자식 노드의 value < 부모 노드 value < 오른쪽 자식 노드 value

3. pseudo Code

/* pseudo Code */
이진탐색트리 {
 left, right, value
  
 method: insert(v) {
	 v값과 비교하여 작으면 left, 크면 right로 진행
     left와 right가 없다면 v를 추가
 }
 
 method: contains {
   	insert에서 각 값을 임시 배열에 담아 저장하여 그 값들과 비교
 }
} 

4. Binary Search Tree Code

코드의 동작 순서를 알아봅시다. 핵심은 Insert코드입니다.

• Insert 순서

1. root(5)가 있음.
2. insert(2) : 2가 5보다 작으므로, left에 추가. left, right === null 이므로 종료
3. insert(3) : 3이 5보다 작으므로, left에 추가 -> left의 2가 3보다 작으므로 right에 추가. left, right === null 이므로 종료
4. insert(7) : 7이 5보다 크므로, right에 추가. left, right === null 이므로 종료
5. insert(6) : 6이 5보다 크므로, right에 추가. -> right의 7이 6보다 크므로 right에 추가. left, right === null 이므로 종료

• Insert 순회 논리

1. root(5)가 있음.
2. insert(4) : 4 < 5 -> (left가 비었는지 -> 비었다. -> 추가)
3. insert(2) : 2 < 5 -> left가 비었는지 -> 안비었다. -> [다시 확인]
   ( [다시 확인] : 2 < 4 -> (left가 비었는지 -> 비었다. -> 추가 ) )

const BinarySearchTree = function(init) {
  const bst = {}
  const checkArray = [init]

  bst.left = null;
  bst.right = null;
  bst.value = init;

  bst.insert = function(v) {
    // 루트노드 5
    if (checkArray.includes(v)) throw new Error('동일한 값은 들어올 수 없습니다.');
    checkArray.push(v)
    const newNode = new BinarySearchTree(v);
    recur(this) // 시작은, rootNode (value: 5)

    function recur(node) {
      let direction = node.value > v ? 'left' : 'right';
      node[direction] === null ? node[direction] = newNode : recur(node[direction]);
    }
  }
  bst.contains = function(v) {
    return checkArray.includes(v)
  }

  bst.depthFirstLog = function(cb) {
    checkArray.forEach((item) => cb(item))
  }

  return bst;
};