자료 구조 중 Graph에 대해서 알아봅니다. 😀

이전 장인 Tree 구조를 공부하고 난 뒤 보면 좋습니다! 용어가 비슷해요~

---

📊 Graph

1. 개념

그래프는 노드와 노드를 연결하는 간선을 하나로 모아놓은 자료 구조입니다.

지하철 노선도를 생각하시는게 좋습니다 :)

용어를 몇가지 정리해봅시다.

1. Vertex(정점) : 트리에서의 노드(node)와 같습니다.
2. Edge(간선) : 트리에서의 가지(branch)와 같습니다.
3. degree(차수) : 무방향 그래프에서 인접한 정점의 두
4. in-degree(진입 차수) : 다른 정점에서 오는 간선의 개수
5. out-degree(차출 차수) : 다른 정점으로 가는 간선의 개수

트리는 하나의 부모 노드에서 아래로 내려오는 그래프라고 할 수 있습니다.

2. 특징

• 네트워크 모델
• 버텍스 사이에서 양쪽 방향으로 방향을 가질 수 있습니다.
• Root / Leaf / 부모 / 자식 등이 없습니다.

3. 종류

• 무방향/방향 그래프 (Undirected/Directed Graph)
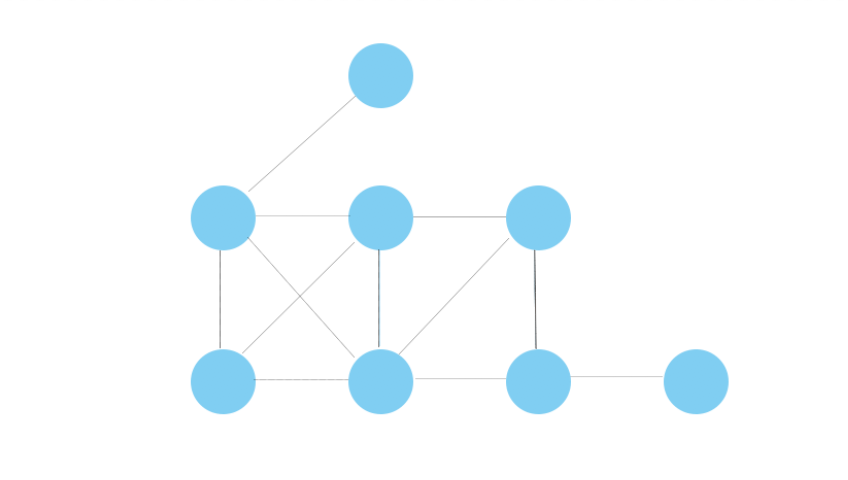
• 무방향 그래프는 아래의 그림처럼 그래프에 화살표가 없습니다!
• 그래서 각 간선은 양방향으로 갈 수 있습니다.
• 반대로 방향 그래프는 아래 그림에서 한쪽으로 화살표가 추가됩니다.
• 사실 트리 구조는 방향 그래프에서 화살표만 생략한 것입니다!

• 가중치 그래프 (Weighted Graph)
• 간선에 비용 또는 가중치가 포함된 그래프입니다.
• 도시간의 연결, 통신망 사용료 등에 사용됩니다.
• 일본 지하철은 구간마다 비용이 증가하는데, 이와 비슷합니다!
• 연결/비연결 그래프(Connected/UnConnected Graph)
• 연결 : 무방향 그래프의 모든 정점간에 항상 경로가 존재하는 경우
• 비연결 : 무방향 그래프의 특정 정점간 경로가 존재하지 않는 경우
• 순환/비순환 그래프 (Cyclic/Acyclic Graph)
• 순환 : 반복되는 정점이 없는 경로에서 시작,종료 정점이 동일한 경우
• 비순환 : 순환이 없는 경우
• 완전 그래프(Complete Graph)
  • 모든 정점이 연결되어 있는 경우

4. pseudo Code

간단하게 동작원리만 생각해봅니다.

// pseudo Code
그래프 {
  store {}, edge {}
  
  method: addNode(값) {
   store에 값을 { '값': 값 }으로 추가한다.
  }
  method: contains(값) {
    store['값'] 이 있는지 조사한다.
  }
  method: removeNode(값) {
   	store['값'] 을 찾아 제거한다.
    제거할 때 연결된 엣지도 제거한다.
  }
  method: hasEdge(from, to) {
   	edge[from] 가 to 인지 찾는다. 
  }
  method: addEdge(from, to) {
   	edge[from]에 to, edge[to]에 from을 추가한다. 
  }
  method: removeEdge(from, to) {
   	delte edge[from], edge[to] 
  }
  method: forEachNode(콜백) {
    store를 돌면서 콜백(값) 을 준다.
  }
}

5. Make Graph

특별한 건 없습니다.

store와 edge객체에 {key: value}형태로 {'값':값}을 넣어 구현합니다.

중요한 점은 노드를 지울 때, 그와 연결된 엣지도 지워야 하는 것입니다.

그렇다면 removeNode에서 연결된 엣지를 찾아서 제거하면 간단합니다 :)

// Graph
const _ = require('underscore')

const Graph = function() {
  this.store = {};
  this.edge = {};
};

Graph.prototype.addNode = function(node) {
  this.store[node] = node;
};

Graph.prototype.contains = function(node) {
  return this.store.hasOwnProperty(node);
};

// 1. 4 --- 5 : 
// 2. 4 ---   : removeNode(5) -> 5랑 뭐가 연결되어있죠? 를 물어봐서 4를 가져온다면,
// 3. 4       : removeEdge(가져온 4, 5),
Graph.prototype.removeNode = function(node) {
  let tmpNode = this.edge[node]
  delete this.store[node]
  this.removeEdge(tmpNode, node)
};

Graph.prototype.hasEdge = function(fromNode, toNode) {
  return this.edge[fromNode] === toNode;
};

Graph.prototype.addEdge = function(fromNode, toNode) {
  this.edge[fromNode] = toNode;
  this.edge[toNode] = fromNode;
};

Graph.prototype.removeEdge = function(fromNode, toNode) {
  delete this.edge[fromNode];
  delete this.edge[toNode];
};

Graph.prototype.forEachNode = function(cb) {
  _.each(this.store, node => cb(node))
};