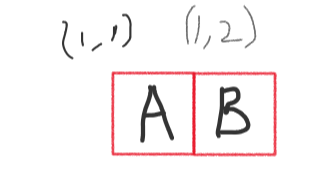https://programmers.co.kr/learn/courses/30/lessons/60063

[1. 문제 이해]

드론의 이동과, 회전에 대해서 완전탐색하면 된다.
편의상 하나의 드론은 두개의 블록으로 이루어져 있다고 할때 두개의 블록은 항상 함께 움직여야한다.
(1)드론이 이동: 상,하,좌,우로 움직일 수 있는 공간 사이에서 움직이면 된다.
(2)드론의 회전: 드론의 회전의 경우에는 드론이 가로인지 세로인지 형태에 따라 변형되게 되는 모습이 달라지므로 신경써야했다.

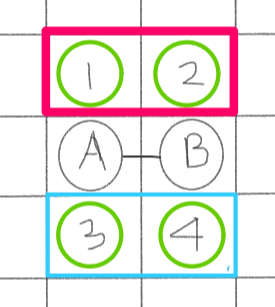
1.블록이 가로 나열한경우

다음 빨간색과 하늘색의 블록의 영역이 드론이 90도 회전할때 접근 할 수 있는 영역이다. 예를들어 B가 회전할때 1번으로 가거나 3번으로 갈 수 있다. 이때 회전해서 도착되어지는 부분뿐만아니라 회전하는 도중 지나는 부분(B가 1번으로 갈때 2번부분)에서도 장애물이 존재하지 않아야한다.
즉 해당색안의 영역에 있는 블록으로 회전 할경우 해당색 안에는 장애물이 있으면 안된다.

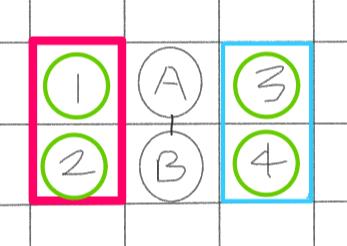
2.블록이 세로 나열한경우.

다음과 같이 세로로 A,B가 나열되어있을경우 회전시 해당 색친영역에 접근 할 수 있고 마찬가지로, 해당색안의 영역에 있는 블록으로 회전 할경우 해당색 안에는 장애물이 있으면 안된다.

[2. 알고리즘 선택]

완전 탐색하는 문제에 있어서 선택할 수 있는 알고리즘은 DFS와 BFS가 있다.

탐색알고리즘 선택

1.DFS: 모든 가능한 루트의 깊이 끝까지에 대해서 다 검색 하므로 비효율적이다. 실제로 시간초과가 발생하였다.

2.BFS: 최소 시간을 구하는 문제에 있어서 BFS가 더 효율적이다. 도착할때마다 매번 최소값을 비교할 필요가 없고 도착순간 바로 return 하면 되기 때문이다.

공간복잡도에 따른 자료형 선택

먼저 백트래킹을 위한 방문체크를 해야한다.
이때 드론의 경우 두개의 블록을 가지고 있고 모든 좌표를 넣게 된다면,

범위: 0<x1, y1, x2, y2<=100
형태: bool visit[x1][x2][y1][y2]
공간복잡도: 최대 100000000Byte=100MB

최대 100Mb이므로 굉장히 비효율적이다. 그렇다면 드론의 특성을 이용해서 조금더 효율적으로 짤 필요가 있다. 드론의 경우는 항상 붙어있고 가로또는 세로의 형태를 뛰고있다. 그렇다면 드론의 하나의 블록과 형태만 뛰게 된다면 어떻게 될까?

범위: 0<=x1,y1<=100,
shape=0(가로),1(세로)
형태: bool visit[x1][x2][shape]
공간복잡도: 20000Byte=20kb

하지만 다음과 같이 만들게 된다면 해당 좌표 x1,y1에 대해서 불명확성이 발생할 수 있다.

예를들어서 생각해보자
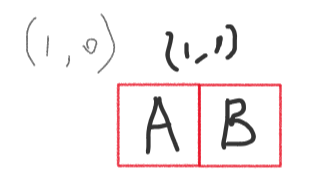
visit[1][1][0:가로]

1번

2번

다음과 같이 블록 A,B가있을때 (1,1)에 해당하는게 A일 수 도있고 B일 수도 있기때문이다.

즉 이를 해결하기 위해서 다음 조건을 상정한다.

드론의 블록인 블록 A(x1,y1) 블록 B(x2,y2) ( x1<=x2, y1<=y2) 에 대하여 항상 A블록의 x1,y1만으로 표시한다.

[2.주요 메서드]

int search(const Board& board)
BFS완전 탐색 탐색한다.

void RotateAndPush(Dron& dron, const Board& board)
해당 드론에 대해서 회전가능한 모든 부분에 관하여 queue에 추가한다.

bool isRange(Dron& dron, const Board& board):
해당드론의 범위에 장애물이 없는지 확인

bool IsVisit(Dron& dron):
해당 드론이 이미 방문했던 드론인지 확인

void Push(Robot& robot):
큐에 드론을 추가하고 방문체크한다.

[3. 구현]

#include <bits/stdc++.h> //https://programmers.co.kr/learn/courses/30/lessons/60063
using namespace std;
#define Board vector<vector<int>>
int MapSize = 0;
bool isVisit[101][101][2] = {true,}; 
int dy[4] = { 0, 0, 1, -1 };
int dx[4] = { 1, -1, 0, 0 }; //오른쪽 왼쪽 아래 위
enum Direction
{
Row = 0, //x2>x1
Col = 1  //y2>y1
};
struct Robot
{
    int x1 = 0, y1 = 0, x2 = 1, y2 = 0, direct = Row, sec = 0; //방향
    Robot() {}
    Robot(int x1, int y1, int x2, int y2, int direct, int sec)
    {
        this->x1 = x1;
        this->y1 = y1;
        this->x2 = x2;
        this->y2 = y2;
        this->direct = direct;
        this->sec = sec;
    }
};
queue<Robot> robots;
int search(const Board& board);
void RotateAndPush(Robot& robot, const Board& board);
bool isRange(Robot& robot, const Board& board);
bool IsVisit(Robot& robot);
void Push(Robot& robot);
int solution(vector<vector<int>> board)
{
    MapSize = board.size();
    return search(board);
}
bool IsVisit(Robot& robot) { return isVisit[robot.y1][robot.x1][robot.direct]; }
void Push(Robot& robot) {
    robots.push(robot);
    isVisit[robot.y1][robot.x1][robot.direct] = true;
}
bool isRange(Robot& robot, const Board& board)
{
    return robot.x1 >= 0 && robot.y1 >= 0 && robot.x2 < MapSize && robot.y2 < MapSize && board[robot.y1][robot.x1] != 1 && board[robot.y2][robot.x2] != 1;
}
void RotateAndPush(Robot& robot, const Board& board)
{
    if (robot.direct == Row)
    { //Row형태일경우
        //robot의 밑부분
        Robot Next_range = robot;
        Next_range.y1 = Next_range.y2 = robot.y1 + 1;
        if (isRange(Next_range, board))
        {
            Robot next_robot(robot.x1, robot.y1, robot.x1, robot.y1 + 1, Col, robot.sec + 1);
            Robot next_robot2(robot.x2, robot.y2, robot.x2, robot.y2 + 1, Col, robot.sec + 1);
            if (!IsVisit(next_robot)) Push(next_robot);
            if (!IsVisit(next_robot2)) Push(next_robot2);
        }
        //robot의 윗부분
        Next_range.y1 = Next_range.y2 = robot.y1 - 1;
        if (isRange(Next_range, board))
        {
            Robot next_robot(robot.x1, robot.y1 - 1, robot.x1, robot.y1, Col, robot.sec + 1);
            Robot next_robot2(robot.x2, robot.y2 - 1, robot.x2, robot.y2, Col, robot.sec + 1);
            if (!IsVisit(next_robot)) Push(next_robot);
            if (!IsVisit(next_robot2))  Push(next_robot2);
        }
    }
    else //Col일경우
    {
        Robot Next_range = robot;
        Next_range.x1 = Next_range.x2 = robot.x1 + 1;
        if (isRange(Next_range, board))
        {
            Robot next_robot(robot.x1, robot.y1, robot.x1 + 1, robot.y1, Row, robot.sec + 1);
            Robot next_robot2(robot.x2, robot.y2, robot.x2 + 1, robot.y2, Row, robot.sec + 1);
            if (!IsVisit(next_robot)) Push(next_robot);
            if (!IsVisit(next_robot2))  Push(next_robot2);
        }
        //robot의 윗부분
        Next_range.x1 = Next_range.x2 = robot.x1 - 1;
        if (isRange(Next_range, board))
        {
            Robot next_robot(robot.x1 - 1, robot.y1, robot.x1, robot.y1, Row, robot.sec + 1);
            Robot next_robot2(robot.x2 - 1, robot.y2, robot.x2, robot.y2, Row, robot.sec + 1);
            if (!IsVisit(next_robot)) Push(next_robot);
            if (!IsVisit(next_robot2))  Push(next_robot2);
        }
    }
}
int search(const Board& board)
{
    robots.push(Robot());
    while (!robots.empty())
    {
        Robot robot = robots.front();
        robots.pop();
        if ((robot.x2 == MapSize - 1 && robot.y2 == MapSize - 1))
        {
            return robot.sec;
        }
        //Go
        for (int i = 0; i < 4; i++)
        {
            Robot next_robot(robot.x1 + dx[i], robot.y1 + dy[i], robot.x2 + dx[i], robot.y2 + dy[i], robot.direct, robot.sec + 1);
            if (isRange(next_robot, board) && !IsVisit(next_robot))  Push(next_robot);
        }
        RotateAndPush(robot, board);
    }
    return 1234567890;
}

[4. 고찰]

RotateAndPush의 경우 상당히 마음에 안들었다.

1. 하나의 함수내에서 두가지 기능을 하고 있다.(회전 그리고 삽입)

이를 어떻게 분리하는게 효율적일지 생각을 해보았는데 하나의 모양(가로 또는 세로) 에 따른 회전형태가 총 4개이기 때문에 Rotate함수와 Push함수를 따로 분리하기가 쉽지 않았다.

2. 사실 코드의 반복이 굉장히 많이 일어남으로써 코드가 복잡해진다.

따라서 Proxy를 이용해서 Aop를 하는게 더 효율적이라고 생각한다.

3. 사실 코딩테스트의 경우 주어진 시간내에 정답을 맞춤을 목표로 한다.

따라서 메서드를 많이 분리시키고 역할을 최대한 쪼개고 분리시키는게 유지보수에는 좋을지라도 오히려 시간적인 면에서 손해 볼 수 있기에 적절한 타협이 필요해보인다.