📚 이진탐색
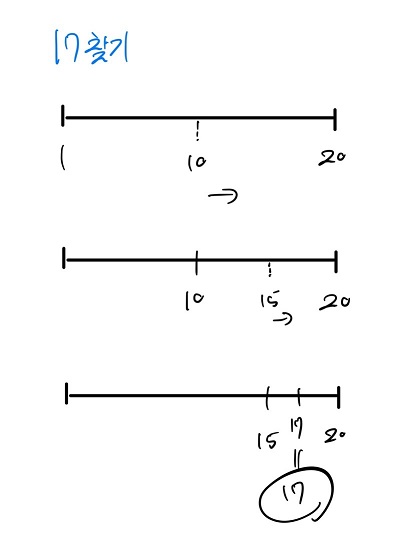
정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
이진탐색은 배열 내부의 데이터가 정렬되어 있어야만 한다
#include <iostream>
#include <vector>
using namespace std;
int n, target;
vector<int> v;
int binarySearch(vector<int>& arr, int target, int start, int end)
{
while (start <= end)
{
int mid = (start + end) / 2;
if (arr[mid] == target)
return mid;
else if (arr[mid] > target)
end = mid - 1;
else
start = mid + 1;
}
return -1;
}
int main ()
{
cin >> n >> target;
for (int i = 0; i < n; i++)
{
int x;
cin >> x;
v.push_back(x);
}
int res = binarySearch(v, target, 0, n - 1);
if (res == -1)
cout << "원소가 존재하지 않습니다." << "\n";
else
cout << res + 1 << "\n";
return 0;
}- 단계마다 탐색 범위를 2로 나누는 것과 동일하기때문에 연산 횟수는 log2N에 비례한다
- 이진 탐색은 탐색 범위를 절반씩 줄이며, 시간 복잡도는 O(logN)을 보장한다
📚 예제
📕 부품찾기
동빈이네 전자 매장에는 부품이 N개 있다. 각 부품은 정수 형태의 고유한 번호가 있다. 어느 날 손님이 M개 종류의 부품을 대량으로 구매하겠다며 당일 날 견적서를 요청했다.동빈이는 때를 놓치지 않고 손님이 문의한 부품 M개 종류를 모두 확인해서 견적서를 작성해야 한다. 이때 가게 안에 부품이 모두 있는지 확인하는 프로그램을 작성해보자.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M;
vector<int> v;
int binarySearch(vector<int> &v, int target, int start, int end)
{
while (start <= end)
{
int mid;
mid = (start + end) / 2;
if (v[mid] == target)
return 1;
else if (v[mid] > target)
end = mid - 1;
else
start = mid + 1;
}
return -1;
}
int main()
{
cin >> N;
for (int i = 0; i < N; i++)
{
int x;
cin >> x;
v.push_back(x);
}
sort(v.begin(), v.end());
cin >> M;
for (int i = 0; i < M; i++)
{
int x;
cin >> x;
if (binarySearch(v, x, 0, N - 1) == 1)
cout << "yes" << " ";
else
cout << "no" << " ";
}
return 0;
}이진탐색을 이용하기 위해서 일단 정렬을 하고 탐색을 하였다 나는 부품을 받으면 하나하나 확인을 하였는데 저자의 코드를 보니 배열로 받은다음 비교하는식으로 하였다
📘 떡볶이 떡 만들기
- 동빈이가 떡볶이 떡을 절단기로 자르는데 떡의 길이가 일정하지가 않다. 대신 한 봉지에 들어가는 떡의 총 길이는 절단기로 잘라서 맞춰준다
- 절단기에 높이(H)를 지정하면 줄지어진 떡을 한 번에 절단한다. 높이가 H보다 긴 떡은 H 우의 부분이 잘릴 것이고, 낮은 떡은 잘리지 않는다
- 예를 들어 높이가 19, 14, 19, 17cm인 떡이 나란히 있고 절단기 높이를 15cm로 지정하면 자른 뒤 떡의 높이는 15, 14, 10, 15cm가 될 것입니다. 잘린 떡의 길이는 차례대로 4, 0, 0, 2cm입니다. 손님은 6cm 만큼의 길이를 가져갑니다.
- 손님이 왔을 때 요청한 총 길이가 M일 때 적어도 M만큼의 떡을 얻기 위해 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M;
vector<int> v;
int main()
{
int start = 0, end, max;
cin >> N >> M;
for (int i = 0; i < N; i++)
{
int x;
cin >> x;
v.push_back(x);
}
sort(v.begin(), v.end());
end = v[N - 1];
while(start <= end)
{
long long int sum = 0;
int mid = (start + end) / 2;
for (int i = 0; i < N; i++)
{
int x;
x = v[i] - mid > 0 ? v[i] - mid : 0;
sum += x;
}
if (sum == M)
{
cout << mid << "\n";
break;
}
else if (sum > N)
start = mid + 1;
else
end = mid - 1;
}
return 0;
}처음생각한 아이디어는 단순히 숫자를 하나하나 넣어보고 모든 떡을 자르면서 내가 원하는 숫자가 나올때까지 탐색하는 방식으로 생각을 했었다 하지만 탐색범위가 너무 넓기 때문에 시간초과가 날 수 있기 때문에 이진탐색을 이용하여 탐색 범위를 줄여주었다.
이런식으로 제일 긴떡을 기준으로 중간점을 잡고 잘린 떡의 길이의 합과 값을 비교하면서 탐색을 시행하였다
➕ 2630 색종이 만들기
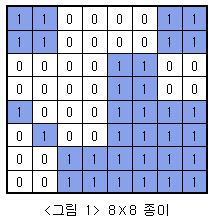
아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.
전체 종이의 크기가 N×N(N=2k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.
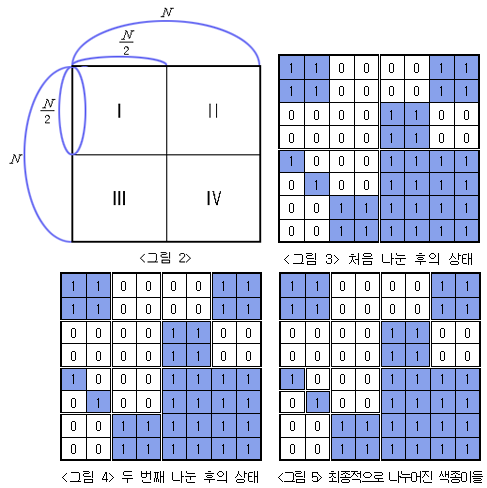
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.
위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.
#include <iostream>
#include <vector>
using namespace std;
int N;
int map[128][128];
int white = 0;
int blue = 0;
void cut(int x, int y, int nx, int ny)
{
int start = map[x][y];
for (int i = x; i < nx; i++)
{
for (int j = y; j < ny; j++)
{
if (start != map[i][j])
{
cut(x, y, (x + nx) / 2, (y + ny) / 2);
cut((x + nx) / 2, y, nx, (y + ny) / 2);
cut(x, (y + ny) / 2, (x + nx) / 2, ny);
cut((x + nx) / 2, (y + ny) / 2, nx, ny);
return;
}
}
}
if (start == 1)
blue++;
else if (start == 0)
white++;
return;
}
int main()
{
cin >> N;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
cin >> map[i][j];
}
cut(0, 0, N, N);
cout << white << "\n" << blue << "\n";
return 0;
}이분탐색문제가 맞는지는 잘 모르겠다 하지만 문제에 주어진대로 파란색으로 이뤄진 사각형, 흰색으로 이뤄진 사각형이 나올때 까지 분할하라고해서 시작점, 끝점, 탐색범위를 설정한 다음에 재귀를 돌렸다 만약 사각형으로 이뤄지지 않았다면 시작점, 끝점, 탐색범위를 새로 지정하여 재귀를 시행하였다 그리고 나온 사각형 개수만큼 카운트해주었다