미로 탈출 문제 보러가기

문제를 해결하는데 사용한 알고리즘

• BFS (너비 우선 탐색)
  • 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다.
    👉 무한루프에 빠질 위험이 있음
  • 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐를 사용한다.
  • Prim, Dijkstra 알고리즘과 유사하다

문제 설명

---

1 x 1 크기의 칸들로 이루어진 직사각형 격자 형태의 미로에서 탈출하려고 합니다. 각 칸은 통로 또는 벽으로 구성되어 있으며, 벽으로 된 칸은 지나갈 수 없고 통로로 된 칸으로만 이동할 수 있습니다. 통로들 중 한 칸에는 미로를 빠져나가는 문이 있는데, 이 문은 레버를 당겨서만 열 수 있습니다. 레버 또한 통로들 중 한 칸에 있습니다. 따라서, 출발 지점에서 먼저 레버가 있는 칸으로 이동하여 레버를 당긴 후 미로를 빠져나가는 문이 있는 칸으로 이동하면 됩니다. 이때 아직 레버를 당기지 않았더라도 출구가 있는 칸을 지나갈 수 있습니다. 미로에서 한 칸을 이동하는데 1초가 걸린다고 할 때, 최대한 빠르게 미로를 빠져나가는데 걸리는 시간을 구하려 합니다.

미로를 나타낸 문자열 배열 maps가 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최소 시간을 return 하는 solution 함수를 완성해주세요. 만약, 탈출할 수 없다면 -1을 return 해주세요.

---

제한사항

• 5 ≤ maps의 길이 ≤ 100
  • 5 ≤ maps[i]의 길이 ≤ 100
  • maps[i]는 다음 5개의 문자들로만 이루어져 있습니다
    • S : 시작 지점
    • E : 출구
    • L : 레버
    • O : 통로
    • X : 벽
  • 시작 지점과 출구, 레버는 항상 다른 곳에 존재하며 한 개씩만 존재합니다.
  • 출구는 레버가 당겨지지 않아도 지나갈 수 있으며, 모든 통로, 출구, 레버, 시작점은 여러 번 지나갈 수 있습니다.

---

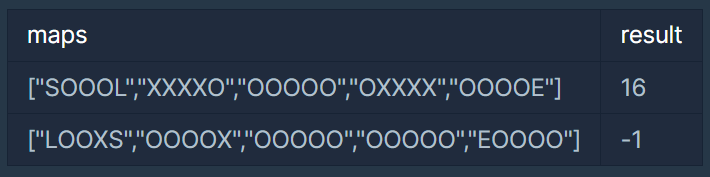
입출력 예

---

핵심 포인트 요약

탐색할 수 있는 조건

• 통로로 된 칸이면 OK
• 레버있는 칸 또한 통로임
  👉 벽빼고 전부다 지나갈 수 있음

• 출발 지점에서 먼저 레버가 있는 칸으로 이동한다음 레버를 당긴 후 미로를 빠져나가는 문이 있는 칸으로 이동하면 됨
  • 출발 지점 --> 레버
  • 레버 --> 출구

👉 즉, 출발 지점에서 레버로, 레버에서 출구로 BFS 알고리즘을 2번 수행 해주면 된다
만약 둘중 하나라도 Path가 존재하지 않는다면(-1을 반환한다면) 최종적으로 -1을 return하면 된다

---

코드 & 설명 주석 포함

from collections import deque

def bfs(start, end, maps):
	# 탐색할 방향
    dy = [0, 1, -1, 0]
    dx = [1, 0, 0, -1]
    
    n = len(maps)       # 세로
    m = len(maps[0])    # 가로
    visited = [[False]*m for _ in range(n)]
    que = deque()
    flag = False
    
    # 초깃값 설정
    for i in range(n):
        for j in range(m):
        	# 출발하고자 하는 지점이라면 시작점의 좌표를 기록함
            if maps[i][j] == start:      
                que.append((i, j, 0))    
                # 별도의 cost 리스트를 만들지 않고 que에 바로 기록(0)
                visited[i][j] = True
                flag = True; break 
                # 시작 지점은 한 개만 존재하기 때문에 찾으면 바로 나옴
        if flag: break
                
    # BFS 알고리즘 수행 (핵심)
    while que:
        y, x, cost = que.popleft()
        
        if maps[y][x] == end:
            return cost
        
        for i in range(4):
            ny = y + dy[i]
            nx = x + dx[i]
            
            # maps 범위내에서 벽이 아니라면 지나갈 수 있음
            if 0<= ny <n and 0<= nx <m and maps[ny][nx] !='X':
                if not visited[ny][nx]:	# 아직 방문하지 않는 통로라면
                    que.append((ny, nx, cost+1))
                    visited[ny][nx] = True
                    
    return -1	# 탈출할 수 없다면
        
            
def solution(maps):
    path1 = bfs('S', 'L', maps)	# 시작 지점 --> 레버
    path2 = bfs('L', 'E', maps) # 레버 --> 출구
    
    # 둘다 -1 이 아니라면 탈출할 수 있음
    if path1 != -1 and path2 != -1:
        return path1 + path2
        
   	# 둘중 하나라도 -1 이면 탈출할 수 없음
    return -1

---

혹시나 잘못된 부분이 있으면 댓글 부탁드립니다.