정수 삼각형 문제 보러가기

동적계획법 알고리즘이란?
여러 개의 하위 문제를 먼저 푼 후 그 결과를 쌓아올려 주어진 문제를 해결하는 알고리즘
👉 중간 결과를 배열에 저장해서 이용하는것이 핵심이다.

DP를 푸는 패턴 간단히 정리 (참고)

1. 테이블 정의하기

• 결과값들을 저장할 배열 정의
• 문제에서 주어진 규칙을 사용해 풀 수 있도록(테이블을 채워나갈 수 있도록) 정의하기

2. 점화식 찾기(패턴 찾기)

• 테이블을 어떤 관계식을 통해 채울지 고민하고 점화식을 찾아 테이블을 채우는 단계
  • 임의의 값을 정해 예시를 들어 전후 관계를 파악
  • 내가 구하고자하는 결과값의 풀이 속에 이전 결과들이 어떤 관계로 들어있는지 파악 (보통 구하고자하는 결과값 속에는 이전 결과값들이 들어있다)
    👉 추가로 테이블에 값을 어디서까지 미리 넣어두고 어디서부터 어디까지 for문으로 돌려서 값을 넣을지도 잘 생각해봐야함

3. 초깃값 정하기

• 테이블의 값을 원활하게 채워나가기 위해 필요한 초깃값

문제 설명

---

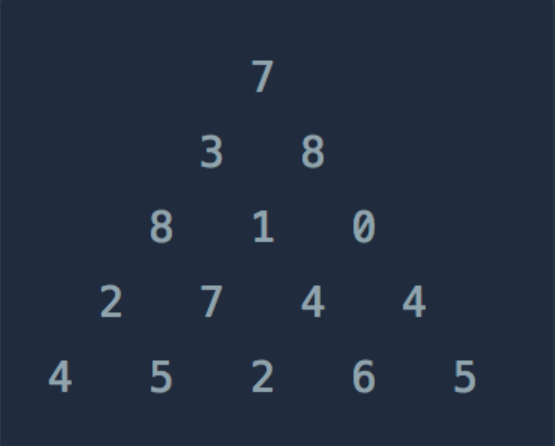
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

---

제한사항

• 삼각형의 높이는 1 이상 500 이하입니다.
• 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

---

입출력 예

---

코드 & 설명 주석 포함

def solution(T):
    n = len(T)
    D = [[0]*i for i in range(1, n+1)]		# 테이블 정의
    D[0][0] = T[0][0]						# 초깃값 설정
    
    # 점화식 찾기 & 테이블 채우기
    for i in range(1, n):
        for j in range(i+1):
			# 삼각형의 가장자리일 경우
            if j == 0:
                D[i][j] = D[i-1][j] + T[i][j]
            elif j == i:
                D[i][j] = D[i-1][j-1] + T[i][j]
            # 삼각형의 중앙 부분일 경우
            else:
                D[i][j] = max(D[i-1][j-1]+T[i][j], D[i-1][j]+T[i][j])
                
    return max(D[-1])

---

혹시나 잘못된 부분이 있으면 댓글 부탁드립니다.