프로그래머스 - 표현 가능한 이진트리 (python)

평범한 대학생·2023년 2월 23일

2023 KAKAO BLIND RECRUITMENT DFS 구현 알고리즘 코딩테스트 프로그래머스

programmers

목록 보기

6/9

표현 가능한 이진트리 문제 보러가기

문제를 해결하기 위해 필요한 지식

트리에 대한 개념

포화이진트리는 무엇인지

루트노드, 리프노드, 서브트리 등에 대한 용어

트리를 탐색하는 방법

DFS

표현 가능한 이진트리 문제풀이 참고

문제 설명

당신은 이진트리를 수로 표현하는 것을 좋아합니다.

이진트리를 수로 표현하는 방법은 다음과 같습니다.

이진수를 저장할 빈 문자열을 생성합니다.
주어진 이진트리에 더미 노드를 추가하여 포화 이진트리로 만듭니다. 루트 노드는 그대로 유지합니다.
만들어진 포화 이진트리의 노드들을 가장 왼쪽 노드부터 가장 오른쪽 노드까지, 왼쪽에 있는 순서대로 살펴봅니다. 노드의 높이는 살펴보는 순서에 영향을 끼치지 않습니다.
살펴본 노드가 더미 노드라면, 문자열 뒤에 0을 추가합니다. 살펴본 노드가 더미 노드가 아니라면, 문자열 뒤에 1을 추가합니다.
문자열에 저장된 이진수를 십진수로 변환합니다.

이진트리에서 리프 노드가 아닌 노드는 자신의 왼쪽 자식이 루트인 서브트리의 노드들보다 오른쪽에 있으며, 자신의 오른쪽 자식이 루트인 서브트리의 노드들보다 왼쪽에 있다고 가정합니다.

다음은 이진트리를 수로 표현하는 예시입니다.

주어진 이진트리는 다음과 같습니다.

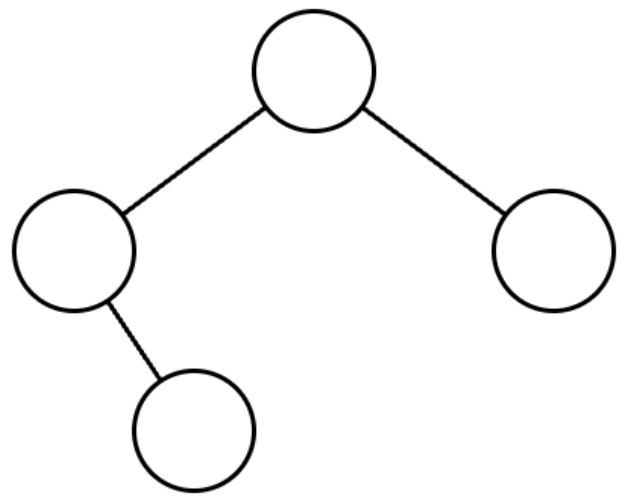
주어진 이진트리에 더미노드를 추가하여 포화 이진트리로 만들면 다음과 같습니다. 더미 노드는 점선으로 표시하였고, 노드 안의 수는 살펴보는 순서를 의미합니다.

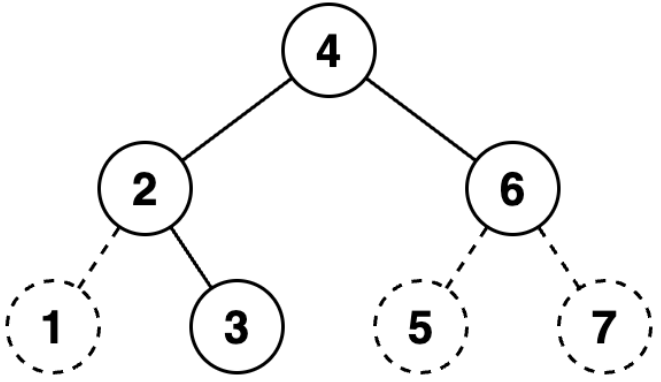
노드들을 왼쪽에 있는 순서대로 살펴보며 0과 1을 생성한 문자열에 추가하면 0111010이 됩니다. 이 이진수를 십진수로 변환하면 58입니다.

당신은 수가 주어졌을때, 하나의 이진트리로 해당 수를 표현할 수 있는지 알고 싶습니다.

이진트리로 만들고 싶은 수를 담은 1차원 정수 배열 numbers가 주어집니다. numbers에 주어진 순서대로 하나의 이진트리로 해당 수를 표현할 수 있다면 1을, 표현할 수 없다면 0을 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해주세요.

제한 사항

1 ≤ numbers의 길이 ≤ $10,000$
- 1 ≤ numbers의 원소 ≤ $10^{15}$

입출력 예

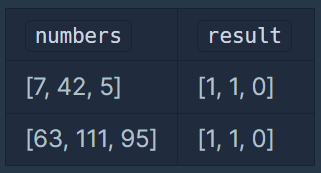
핵심 포인트 요약

문제유형
구현 문제로 여러개의 작은 단위로 문제를 쪼개서 하나씩 순서대로 문제를 해결해야 한다. 문제 설명에서 주어진 번호 순서대로 따라가면서 구현하면 되는 문제이다.

문제에서 주어진 numbers을 이진수로 변환 해야한다.
- 42 -> 101010
변환한 이진수를 포화이진트리 형태로 만들어 준다.
- 포화이진트리로 만든다는 것은 현재 변환한 이진수의 길이를 전체 트리 노드의 수라고 했을 때 포화이진트리가 갖는 최소 노드의 수로 맞춰주라는 뜻이다
- 101010을 예로 들면 현재 길이는 6 즉 노드의 수가 6개다
- 가장 가까운 포화이진트리의 노드의 수는 7개로 더미노드를 1개 추가해야한다.
- 이때 42라는 원래 수의 크기는 변하면 안되기 때문에 포화이진트리의 노드의 수에서 현재 길이(노드 수)를 뺀 숫자만큼 더미노드(0)를 앞에 추가해준다.
포화이진트리인지 아닌지 판단
- 이 과정에서는 포화이진트리가 맞는지 아닌지 검사해서 맞으면 1 틀리면 0 을 배열에 담아준다.
- DFS 탐색 알고리즘을 사용한다.
- 부모노드가 더미노드(0) 일때 자식노드가 더미노드가 아니라면(1) 이진트리로 해당 수를 표현할 수 없다.

코드 & 설명 주석 포함

def dfs(b, i, depth):
    if depth == 0:  	# 리프 노드에 도달했다면
        return True 	# 포화이진트리
    
    # 부모노드가 '0' 일때
    # 왼쪽 자식 노드가 '1' 이거나 오른쪽 자식 노드가 '1' 이라면 포화 이진트리가 될 수 없음
    elif b[i] == '0':   
        if b[i - depth] == '1' or b[i + depth] == '1': return False

    # 왼쪽 서브 트리 탐색
    left = dfs(b, i - depth, depth // 2)
    # 오른쪽 서브 트리 탐색
    right = dfs(b, i + depth, depth // 2)
    return left and right
    
    
def solution(numbers):
    answer = []
    for num in numbers:				# num = 42
        b = bin(num)[2:]  			# b = 101010 / len(b) = 6
        nodes = bin(len(b) + 1)[2:] 	# nodes = 7 = 111
        
        # 포화이진트리가 아닌 경우 더미노드(0추가)
        if '1' in nodes[1:]:       
            dummies = (1 << len(nodes)) - int(nodes, 2)
            b = '0' * dummies + b
            
        # 이미 포화이진트리일 경우
        result = dfs(b, len(b)//2, (len(b)+1)//4)
        answer.append(1 if result else 0)
        
    return answer

보충 요약

포화이진트리에서 노드 개수에 대한 이진수 패턴 표현

첫번쨰 포화이진트리 :

노드개수가 1개 일때, 이진수로 : 1

두번째 포화이진트리 :

노드개수가 1+2=3개 일때, 이진수로 : 11 = 100-1

세번째 포화이진트리 :

노드개수가 1+2+4=7개 일때, 이진수로 : 111 = 1000-1

네번째 포화이진트리 :
- 노드개수가 1+2+4+8=15개 일때, 이진수로 : 1111 = 10000-1

포화이진트리에서 노드 개수와 인덱스 & 깊이 관계 (서브트리의 인덱스를 설정하기 위해서 생각해봐야 할 부분)

포화이진트리에서 마지막 트리 레벨에서의 부모노드와 자식노드2개(왼쪽,오른쪽)로 이루어진 트리의 개수 : depth = (노드 개수 + 1) // 4

루트 노드의 인덱스 i 라고 할때

왼쪽 자식 노드의 인덱스 : i - depth//2

오른쪽 자식 노드의 인덱스 : i + depth//2

👉 이 문제의 경우 트리를 탐색할때 주어진 10진수를 포화이진트리 형태인 이진수 문자열로 바꾼다음 가운데 인덱스(루트 노드) 부터 시작하기 때문에 서브트리의 인덱스를 어떻게 설정해나가야 하는지 잘 생각해야 한다.

👉 포화이진트리에서 전체 노드의 개수는 n번째 일때 $2^n -1$

노드개수가 주어졌을 때 포화이진트리를 만족하려면 "노드개수 = $2^n -1$ " 가 성립해야함

따라서 노드개수 + $1$ = $2^n$ 가 되고
$2^n$ 는 1, 10, 100, 1000, 10000 ... 형태로 첫번째자리를 제외하고 전부다 0인것을 알 수 있다. 이를 이용해서 우리는 포화이진트리인지 아닌지 판단할 수 있게 된다.