
합승 택시 요금 문제 보러가기
문제를 해결하는데 사용한 알고리즘
- 다익스트라 알고리즘 사용
- 플로이드-워셜 알고리즘으로도 해결 가능
- 전형적인 최단거리 구하는 문제 였음
문제 설명
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.
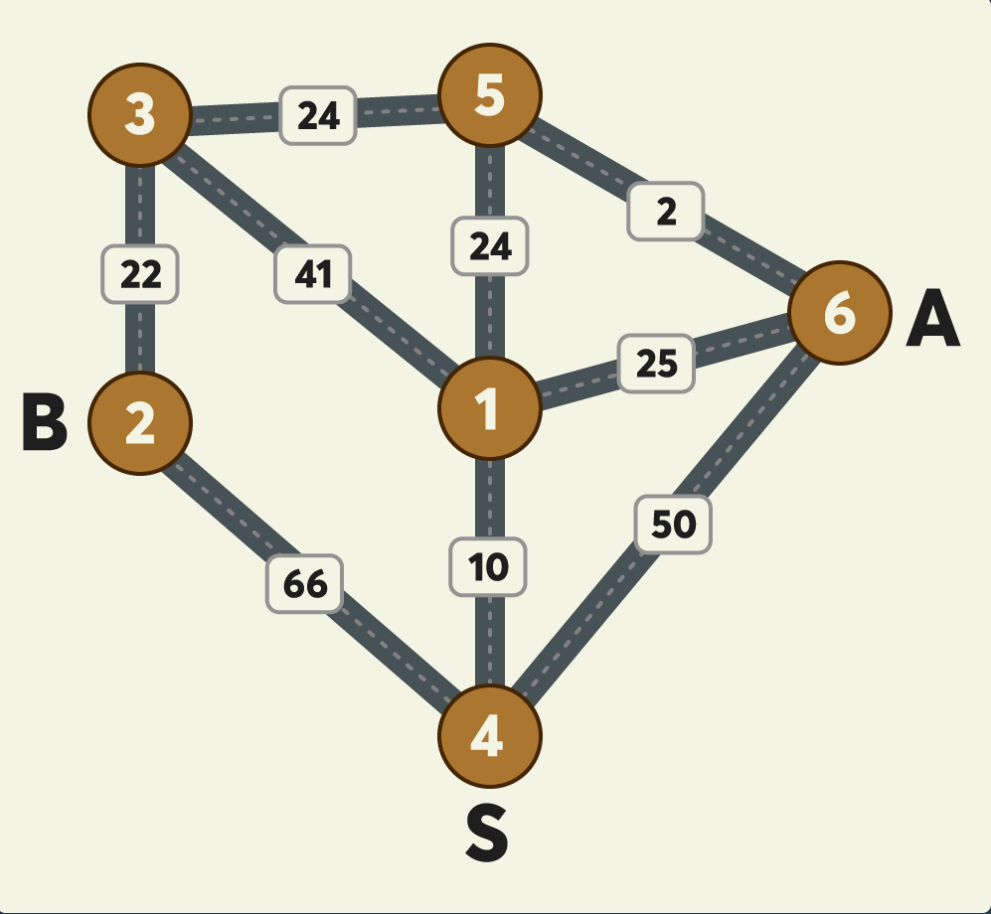
위 예시 그림은 택시가 이동 가능한 반경에 있는 6개 지점 사이의 이동 가능한 택시노선과 예상요금을 보여주고 있습니다.
그림에서 A와B 두 사람은 출발지점인 4번 지점에서 출발해서 택시를 타고 귀가하려고 합니다. A의 집은 6번 지점에 있으며 B의 집은 2번 지점에 있고 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 합니다.
- 그림의 원은 지점을 나타내며 원 안의 숫자는 지점 번호를 나타냅니다.
- 지점이 n개일 때, 지점 번호는 1부터 n까지 사용됩니다.
- 지점 간에 택시가 이동할 수 있는 경로를 간선이라 하며, 간선에 표시된 숫자는 두 지점 사이의 예상 택시요금을 나타냅니다.
- 간선은 편의 상 직선으로 표시되어 있습니다.
- 위 그림 예시에서, 4번 지점에서 1번 지점으로(4→1) 가거나, 1번 지점에서 4번 지점으로(1→4) 갈 때 예상 택시요금은 10원으로 동일하며 이동 방향에 따라 달라지지 않습니다.
- 예상되는 최저 택시요금은 다음과 같이 계산됩니다.
- 4→1→5 :
A,B가 합승하여 택시를 이용합니다. 예상 택시요금은10 + 24 = 34원 입니다. - 5→6 :
A가 혼자 택시를 이용합니다. 예상 택시요금은2원 입니다. - 5→3→2 :
B가 혼자 택시를 이용합니다. 예상 택시요금은24 + 22 = 46원 입니다. A,B모두 귀가 완료까지 예상되는 최저 택시요금은34 + 2 + 46 = 82원 입니다.
- 4→1→5 :
문제
-
지점갯수 n은 3 이상 200 이하인 자연수입니다.
-
지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 즉, 출발지점,
A의 도착지점,B의 도착지점은 서로 겹치지 않습니다.
- 즉, 출발지점,
-
fares는 2차원 정수 배열입니다.
-
fares 배열의 크기는 2 이상
n x (n-1) / 2이하입니다.- 예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (
6 x 5 / 2 = 15) - fares 배열의 각 행은 [c, d, f] 형태입니다.
- c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
- 지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 요금 f는 1 이상 100,000 이하인 자연수입니다.
- fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, [c, d, f]가 있다면 [d, c, f]는 주어지지 않습니다.
- 예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (
-
출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.
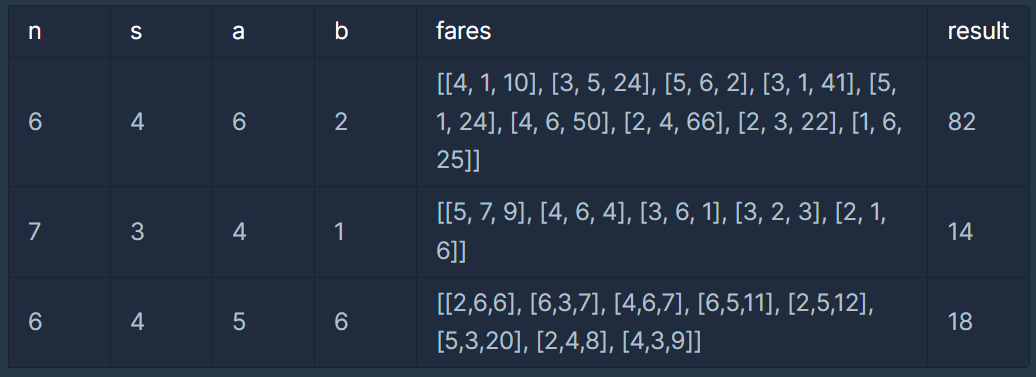
입출력 예
핵심 포인트 요약
- 출발지점(
S)이 정해져있고, 도착 지점(A,B) 또한 정해져 있다.
👉 이때 경우의 수를 생각해보면 출발지점에서 출발하여 다른 지점을 거치지 않고 바로 A, B지점으로 가는 경우를 생각해볼 수 있고 (각각 혼자 택시를 탑승하는 경우라고 생각하면 된다)
👉 또는 하나의 지점을 거치고 A, B 지점으로 가는 경우를 생각해볼 수 있다. 이때 하나의 지점을 거치고 A, B로 가게 되는 경우는 하나의 지점까지는 A, B가 합승하여 택시를 이용한다고 생각할 수 있다
- 따라서, 특정한 하나의 정점(출발지점
S)에서 다른 모든 정점(우리가 구하고자하는 것은 도착지점A,B)으로 가는 최단 경로를 구할 수 있는 다익스트라 알고리즘 또는 플로이드 워셜 알고리즘을 사용하면 된다.
코드 & 설명 주석 포함 (다익스트라 사용)
import sys, heapq
def solution(n, s, a, b, fares):
INF = sys.maxsize
# 문제에서 주어진 fares를 인접리스트 형태로 바꿈
maps = [[] for _ in range(n+1)]
for v,u,c in fares:
maps[v].append((u, c))
maps[u].append((v, c))
# 다익스트라 알고리즘으로 구현
def dijkstra(start):
distance = [INF] * (n+1)
distance[start] = 0
que = [(0, start)]
while que:
cur_dist, cur_node = heapq.heappop(que)
if distance[cur_node] < cur_dist:
continue
for next_node, next_dist in maps[cur_node]:
if distance[next_node] > cur_dist + next_dist:
distance[next_node] = cur_dist + next_dist
heapq.heappush(que, (cur_dist + next_dist, next_node))
return distance
# i번째(특정 노드)에서 시작해서 모든 정점으로 도착하는 최단거리를 미리 구함
D = [0] + [dijkstra(i) for i in range(1, n+1)]
path = INF
for i in range(1, n+1):
path = min(path, D[s][i] + D[i][a] + D[i][b])
return path보충 설명
# i번째(특정 노드)에서 시작해서 모든 정점으로 도착하는 최단거리를 미리 구함
D = [0] + [dijkstra(i) for i in range(1, n+1)]
path = INF
for i in range(1, n+1):
path = min(path, D[s][i] + D[i][a] + D[i][b]) 👉 우리가 구하고자 하는 최소 거리비용(최저 택시요금)
출발점s에서 i까지의 거리 + i에서 a까지의 거리 + i에서 b까지의 거리
s(출발점)랑i가 같다면 각각 혼자 택시를 탑승하게 되는 경우라 볼 수 있고 만약s(출발점)랑i가 다르다면s부터i까지는A,B가 합승하여 택시를 이용하는 거라고 생각할 수 있다.
혹시나 잘못된 부분이 있으면 댓글 부탁드립니다.
