해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로,
모든 출처는 https://www.lgaimers.ai/입니다.
연속형 수명분포와 신뢰성 척도
이번 시간에는, 각 분포들이 갖는 의미와 고장에 대해 알아보았다.
지수분포

지수분포의 특징으로는, 시간 t에 관계없이 원래의 평균수명과 동일하여 지수분포를 따르는 제품은 작동하는 동안에는 늘 새것(as good as new)와 같다고 생각하는 망각성(memoryless property)이 존재하는 것이다.
그로 인해 마모의 개념을 적용할 수 없는 분포이며, 지수분포의 무기억성 (Memoryless Property of Exponential Distribution)은 다음과 같이 설명할 수 있다.
시간 S까지 고장이 발생하지 않고 살아있는 제품이 시간 S+T까지 고장이 발생하지 않고 살아있을 확률은 고장시점 S나 T와도 무관하게 시점의 차이인 T까지 고장이 발생하지 않고 살아있을 확률로 표현한다.
확률변수 X가 지수분포를 따를 때 양의 실수 s, t에 대해 다음이 성립한다.
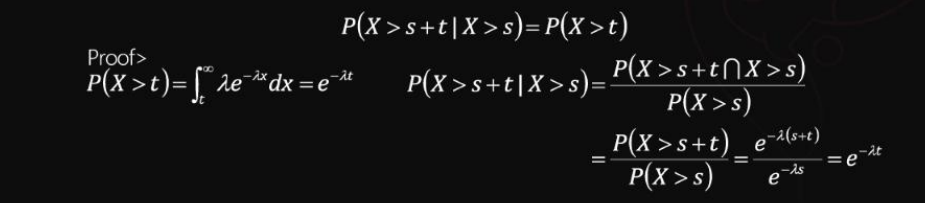
예를 들어, 버스 도착이간이 지수분포 l = 6대/시간을 따른다고 가정하고, 정류장에서 5분을 기다렸는데 아직 버스가 오지 않았다면, 다음 2분을 더 기다려서 버스가 도착할 확률은 처음 정류장에 도착해서 2분동안 기다렸을 때 버스가 도착할 확률과 같다.
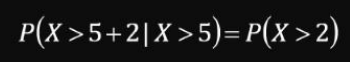
지수분포는 일반적으로 사건이 1개 발생하는데 걸리는 시간에 대한 분포로 사용되는데, 이 때 사건의 발생빈도
l > 0는 포아송분포와 지수분포에서 모두 동일한 의미로 사용된다.
포아송분포: 발생빈도에 따라 단위시간동안 발생하는 사건의 수가 확률변수지수분포: 발생빈도에 따라 1개의 사건이 발생하는 데 걸리는 시간이 확률변수
확률변수 X를 발생빈도 l > 0인 포아송 프로세스에서 첫 번째 사건이 발생하는데 걸리는 시간이라고 하면, 이 시간은 지수분포를 따른다.

즉, 포아송 프로세스에서 사건의 발생 시간간격은 지수분포를 따른다.
다음은 지수분포의 예를 보인다.
어떤 부품의 수명 T가 지수분포 (l = 0.2/년)를 따른다고 알려져 있을 때, 이 부품이 서로 다른 5개의 제품에 장착되었고 8년 후에 그 중 적어도 2개의 부품이 동작하고 있을 확률은?
- 개별 부품 한 개가 8년 동안 고장나지 않을 확률은 다음과 같다.
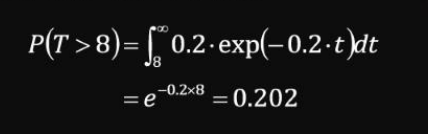
5개의 제품에 각각 장착된 부품 중 2개가 고장나지 않을 확률은 시행횟수가 5회, 성공확률이 0.202인 이항분포로 계산되어, 고장난 부품의 개수를 X라고 했을 때 아래와 같이 계산된다.

- 지수분포를 따르는 제품에 대한 고려사항
- 사용된 제품은 확률적으로 새 것과 같이 때문에, 작동하고 있는 부품을 예방보전의 목적으로 미리 교체할 이유가 없다.
- 신뢰도함수, 고장까지의 평균시간 등의 추정은 관측시점에서 부품들의 총 작동시간과 고장의 수에 대한 데이터를 수집하는 것만으로도 충분하다.
- 장점 및 사용
Drenick의 정리: 여러 개의 다른 형태의 부품으로 구성되어 만들어진 복잡한 기기나 시스템의 수명분포는 비교적 넓은 조건하에서 근사적으로 지수분포를 따옴- 수학적으로 다루기 쉬우며, 전기 및 전자부품 고장의 모형화에 많이 사용
감마분포 (Erlang Distribution)
서로 독립인 확률변수 X1, X2,... XK가 모수 (l > 0) 인 지수분포를 따를 때, X들의 합은 감마분포를 따른다.
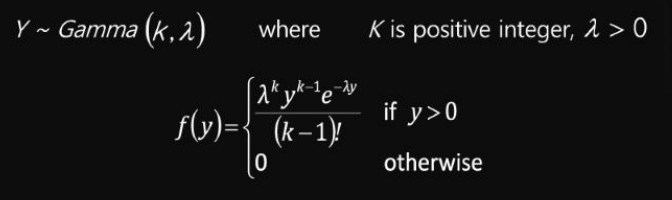
감마분포의 기댓값과 분산은 다음과 같다.
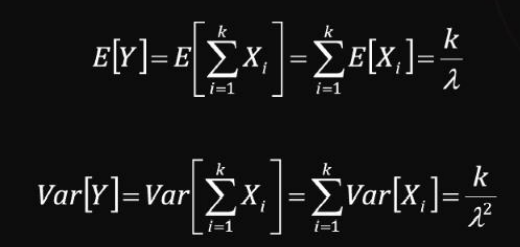
포아송 프로세스를 따르는 사건 K건이 발생하는 데 걸린 시간의 확률분포 -> 감마분포(k, l)
시간 lt동안 포아송 프로세스를 따르는 사건의 개수에 대한 확률분포 -> 포아송분포(lt)
다음은 감마분포의 예다.
- 어떤 가게에 포아송 프로세스를 따라 시간당 평균 30명의 고객이 방문할때, 처음 두 명의 고객이 방문할 때 까지 가게 주인이 기다리는 시간이 5분 이상일 확률을 구해라.
- 방문하는 손님 수는
l=0.5/분인 포아송 프로세스를 따르며, 2건의 고객이 방문하는 데 걸리는 시간을 확률변수 X라 할 때X~gamma(k=2, l=0.5)다.
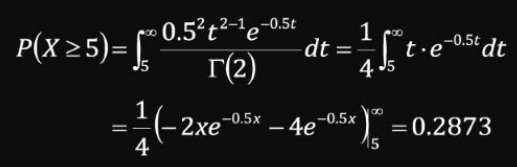
- 평균 수명이 500시간이고 지수분포를 따르는 센서가 있을 때, 센서의 작동여부를 연속적으로 확인할 수 없기 때문에 10시간마다 검사를 진행한다. 이 때 다섯 번째 검사에서 고장이 발견될 확률은?
-
평균수명 500시간인 지수분포를 따르므로, 10시간 이내에 고장날 확률
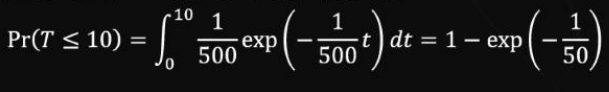
-
지수분포는 무기억성을 가지므로, 이전 구간에서 고장이 발생하지 않았다면 다음 구간에서 고장이 발생할 확률은 일정하다고 간주한다. 따라서, 다섯 번째에 고장이 발생할 확률은 다음과 같다.
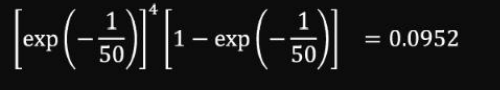
와이블 분포 (Weibull Distribution)
확률변수 X가 다음의 확률밀도함수를 가질 때, 와이블분포를 따른다고 한다.

- 알파는
척도모수(Scale Parameter), 베타는 `형상모수(Shape Parameter)라고 한다. - 형상모수가 1인 경우 와이블 분포는 지수분포와 동일하다.
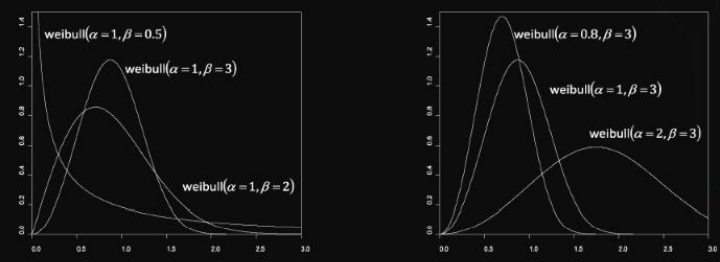
와이블 분포의 기댓값과 분산은 다음과 같다.
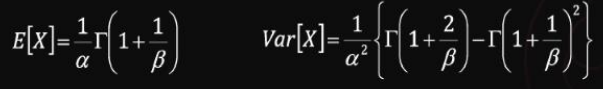
와이블 분포의 주요 속성을 정리하면 다음과 같다.

특징으로는,
- 신뢰성 데이터 분석에 가장 널리 사용되는 분포이며, 형상모수 베타에 의해 분포의 형태가 달라지고 다른 분포로 변환된다.

-
최약 연결(weakest link) 법칙: 독립적이고 동일한 분포를 따르는 여러 개의 비음의 확률변수들이 있을 때, 최소인 확률변수의 분포는 와이블분포를 따르게 된다. -
지수분포는 어셈블리와 시스템의 수명분포를 나타내는 데 주로 사용하며, 와이블분포는 부품의 수명분포에 주로 사용된다.
와이플분포의 예는 다음과 같다.
- 헤드 램프의 수명 T는 형상모수 베타 = 2.25와 척도모수
l = 1.15 * 10^-4인 와이블 분포를 따른다고 할 때, 이 램프가 연속적으로 6개월 (t=4380)동안 생존하게 될 확률은
이고, 평균수명과 메디안 수명은 각각
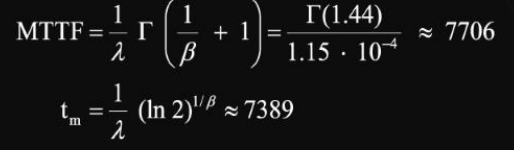
이며, 처음 6개월 동안 생존한 램프가 다음 6개월 동안 생존할 확률은
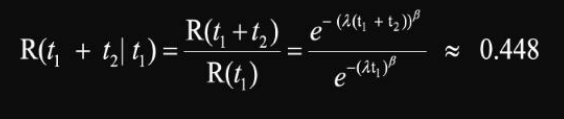
이다.
정규분포
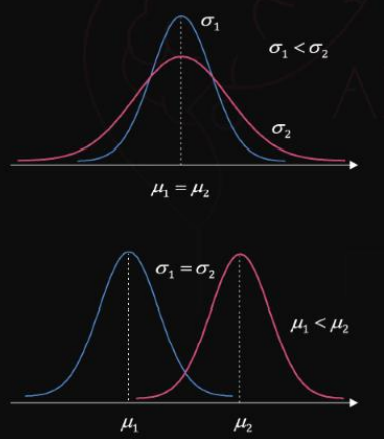
정규분포의 pdf는 중심이 뮤이고, 좌우대칭인 종모양의 형태를 갖으며, 시그마 제곱은 분포의 넓고 좁은 정도를 결정하는 모수다.
평균이 0이고 분산인 1인 정규분포를 표준정규분포(Standard Normal Distribution)라고 하고, 식은 다음과 같다.

표준정규분포를 따르는 확률변수 z에 대한 파이(z) 값을 알고 있으면, 모든 정규분포의 확률계산을 할 수 있다.
-
정규분포의 큰 특징중 하나는, N이 충분히 클 경우 표본평균의 분포는 표본이 추출된 분포에 상관없이 근사적으로 정규분포를 따른다는 점으로, 다시 말해 독립이며 동일한 분포를 따르는 확률변수들의 평균은 항상 근사적으로 정규분포를 따른다는 것이다.
-
일반적으로 n이 25~30보다 클 경우 정규분포에 충분히 근사하다고 판단하며, 표본이 추출된 원래 분포가 좌우 대칭인 연속형 분포라면 n이 4~5정도로 아주 작더라도 충분히 정규분포에 근사하다. 또한, 원래 분포가 정규분포라면, n이 2~3만 되어도 정규분포에 아주 근사하다.
대수정규분포 (Lognormal Distribution)
확률변수 Y가 정규분포를 따를 때, 확률변수 X는 대수정규분포를 따른다.
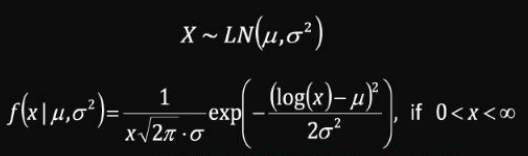
일반 정규분포와 달리 대수정규분포는 다양한 형태의 분포를 표현할 수 있기 때문에, 고장데이터 등을 모형화 하는 경험적 모형으로 폭넓게 사용된다. 또한, 정규분포 확률변수에 단순히 대수만 취하면 되어, 정규분포의 다양한 성질들을 사용할 수 있다.
- 곱셉형 충격(Multiplicative Shocks)의 누적효과로 인해 고장이 발생하는 현상에 대해서 대수정규분포가 유도됨을 보일 수 있다. (반도체 고장, 금속 부식, 크랙 등)
Bernoulli와 이항 분포(Binomoal Distribution)
결과값이 성공과 실패로 나누어지는 실험을 수행했다고 가정할 때, 결과값이 성공인 경우 X는 1, 실패의 경우 0이라고 할 때, pmf가 다음과 같은 확률변수를 베르누이 확률변수라고 한다.
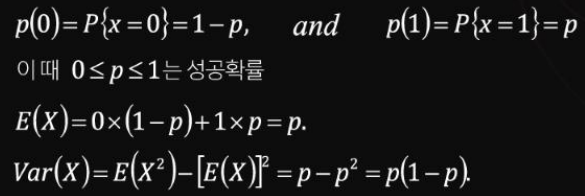
만약, n개의 독립적인 베르누이 시행을 X1, X2,...,X_n이라 하고, 각각의 X가 1의 값을 가질 확률을 p라고 하면, Y=X1+...+X_n은 모수 n과 p를 갖는 이항분포를 가지며, y~B(n, p)로 나타낸다.

독립적인 베르누이 시행의 합으로 이항 확률변수를 고려하면, 다음과 같다.
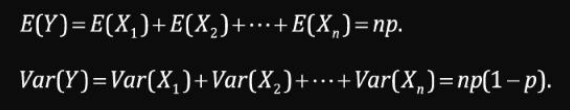
예를 들어, 4개의 동전을 던졌을 경우 각각의 동전의 결과는 서로 독립이라고 가정한다면, 2개는 앞면 2개, 2개는 뒷면이 나올 확률은 얼마인가? -> X~B(4, 1/2)

포아송 분포(Poisson Distribution)
일정한 단위 시간 동안에 발생하는 사건의 수에 대해 관심이 있을 때, 확률변수를 표현하고자 고안한 분포로, 단위 시간 동안 발생빈도가 l인 포아송 프로세스를 다르는 사건의 발생 회수를 X라고 하면, 주어진 t시간 동안 발생하는 사건의 수는 평균 u = lt인 포아송 분포를 따른다.
- 어느 실섬실 실험에서 1ms당 통과하는 방사성 물질의 평균 수가 4일 때, 특정 1ms 동안 6개의 방사성 물질이 통과할 확률은 얼마인가?
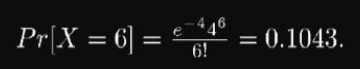
- 특정 S/W에 포함되어 있는 에러의 수는
l=3인 포아송분포를 따른다. 에러가 하나도 없을 확률과 3개 이상의 에러를 포함할 확률을 구하라.
