Deep Learning I 5강

Deep Learning I 5강 신경망 구현

5강에서는 배치묶음 처리의 개념과 배치(묶음)을 어떻게 코드로 구현할 수 있는지에 대해 학습했습니다.

왜 배치(묶음) 처리를 해야 하는가?

딥러닝에서는 한번에 많은 데이터를 효과적으로 학습하기 위해 배치(묶음) 처리를 합니다. 학습 데이터를 하나하나 처리 할 경우 학습하는데 오랜 시간이 걸리고 리소스를 효율적으로 사용할 수 없기 때문입니다. 이때 한번에 처리할 데이터의 수를 batch size라고 합니다. 만약 batch size가 100이라면 한번에 100개의 데이터를 학습시킨다는 의미입니다. 배치 처리가 왜 효율적인지는 아래의 식을 통해 살펴보겠습니다.

$\begin{pmatrix}a^{(1)}_{1}&a^{(1)}_{2}&a^{(1)}_{3}\end{pmatrix}$ = $\begin{pmatrix}x_1&x_2\end{pmatrix}$$\begin{pmatrix}w^{(1)}_{11}&w^{(1)}_{12}&w^{(1)}_{13}\\w^{(1)}_{21}&w^{(1)}_{22}&w^{(1)}_{23}\end{pmatrix}$ + $\begin{pmatrix}b^{(1)}_{1}&b^{(1)}_{2}&b^{(1)}_{3}\end{pmatrix}$

$\begin{pmatrix}a'^{(1)}_{1}&a'^{(1)}_{2}&a'^{(1)}_{3}\end{pmatrix}$ = $\begin{pmatrix}x'_1&x'_2\end{pmatrix}$$\begin{pmatrix}w^{(1)}_{11}&w^{(1)}_{12}&w^{(1)}_{13}\\w^{(1)}_{21}&w^{(1)}_{22}&w^{(1)}_{23}\end{pmatrix}$ + $\begin{pmatrix}b^{(1)}_{1}&b^{(1)}_{2}&b^{(1)}_{3}\end{pmatrix}$

$\begin{pmatrix}a''^{(1)}_{1}&a''^{(1)}_{2}&a''^{(1)}_{3}\end{pmatrix}$ = $\begin{pmatrix}x''_1&x''_2\end{pmatrix}$$\begin{pmatrix}w^{(1)}_{11}&w^{(1)}_{12}&w^{(1)}_{13}\\w^{(1)}_{21}&w^{(1)}_{22}&w^{(1)}_{23}\end{pmatrix}$ + $\begin{pmatrix}b^{(1)}_{1}&b^{(1)}_{2}&b^{(1)}_{3}\end{pmatrix}$

만약 배치 처리를 하지 않는다면 위와 같이 식을 세개로 나눠 계산해야 합니다. 한눈에 보기에도 식을 계산하기 까다롭다는 것을 알 수 있습니다. 하지만 배치 처리를 한다면 아래와 같이 식이 깔끔하게 정리된다는 것을 알 수 있습니다.

$\begin{pmatrix}a^{(1)}_{1}&a^{(1)}_{2}&a^{(1)}_{3}\\a'^{(1)}_{1}&a'^{(1)}_{2}&a'^{(1)}_{3}\\a''^{(1)}_{1}&a''^{(1)}_{2}&a''^{(1)}_{3}\end{pmatrix}$ = $\begin{pmatrix}x_1&x_2\\x'_1&x'_2\\x''_1&x''_2\end{pmatrix}$$\begin{pmatrix}w^{(1)}_{11}&w^{(1)}_{12}&w^{(1)}_{13}\\w^{(1)}_{21}&w^{(1)}_{22}&w^{(1)}_{23}\end{pmatrix}$ + $\begin{pmatrix}b^{(1)}_{1}&b^{(1)}_{2}&b^{(1)}_{3}\\b^{(1)}_{1}&b^{(1)}_{2}&b^{(1)}_{3}\\b^{(1)}_{1}&b^{(1)}_{2}&b^{(1)}_{3}\end{pmatrix}$

따라서 한번에 많은 학습 데이터를 처리해야 하는 딥러닝에서는 배치 처리를 이용하는 것이 더 효율적임을 알 수 있습니다. 추가로 수강중인 강의의 과제 중에 batch size가 1~30일 때 처리 속도를 비교하는 코드를 작성하는 과제가 있습니다. 그 과제를 통해 아래 그림과 같이 batch size가 늘어날수록 처리 속도가 증가한다는 것을 알 수 있습니다.

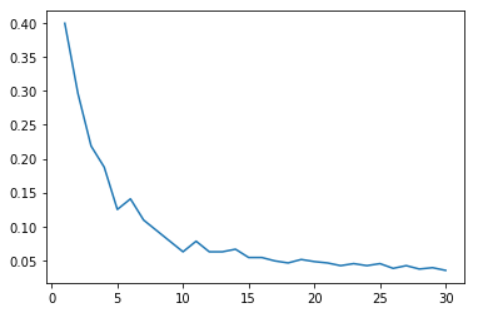
코드로 구현한 배치(묶음) 처리

우선 과제를 위해 작성했던 코드를 살펴보겠습니다. 이 코드에서의 활성화 함수는 ReLU를 이용했습니다. bahtch size는 3이며 가중치와 편향값은 과제에서 정해준 값을 입력하였습니다.

import numpy as np

def ReLU(x):
    return np.maximum(0, x)

def softmax(x):
    if x.ndim==2:
        x=x.T
        x=x-np.max(x, axis=0)
        y=np.exp(x)/np.sum(np.exp(x), axis=0)
        return y.T
    
    x=x-np.max(x)
    return np.exp(x)/np.sum(np.exp(x))

def init_network():
    network = {}
    network['W1'] = np.array([[0,0,0,0,1],[-1,0,0,0,0],[0,-1,0,0,0],[0,0,-1,0,0],[0,0,0,-1,0]])
    network['b1'] = np.array([5,4,3,2,1])
    network['W2'] = np.array([[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0],[0,0,0,0,1],[1,0,0,0,0]])
    network['b2'] = np.array([-1,-2,0,0,0])
    
    return network

def forward(network, x):
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    a1 = np.dot(x,W1)+b1
    z1 = ReLU(a1)
    a2 = np.dot(z1,W2)+b2
    y = softmax(a2)
    
    return y

network = init_network()
x = np.array([[1,2,3,4,5],[2,3,4,5,6],[3,4,5,6,7]])
y = forward(network, x)
print(y)

위에서 쓴 식에서 살펴본 것과 같이 다음으로는 과제에서 나왔던 코드를 살펴보도록 하겠습니다.

import time
import matplotlib.pyplot as plt

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("파일 위치", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, w2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, w3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()

batch_size = np.arange(1,31)
elapse = []

for k in batch_size:
    accuracy_cnt = 0
    start=time.time()
    for i in range(0, len(x), k):
        x_batch = x[i:i+k]
        y_batch = predict(network, x_batch)
        p = np.argmax(y_batch, axis=1)
        accuracy_cnt += np.sum(p == t[i:i+k])
    elapse.append(time.time()-start)

위에서 언급했던 batch size에 따른 처리 속도의 차이를 살펴보는 코드입니다. 학습 데이터를 배치 처리를 하면서 달라지는 부분은 위 코드의 for i in range(0, len(x), k):부터 입니다. 이 코드를 통해 한번에 불러올 데이터의 범위를 지정할 수 있습니다. k의 값이 batch size이므로 0부터 len(x)까지 batxh size만큼 i가 증가하게 됩니다. 다음으로 배치 처리를 할 때는 행렬식을 입력해야 하므로 x_batch = x[i:i+k]와 같이 코드를 작성해줍니다. x_batch에 입력된 값은 y_batch = predict(network, x_batch)를 통해 값을 예측하게 됩니다. 신경망이 예측한 결과가 정답인지는 p = np.argmax(y_batch, axis=1)와 accuracy_cnt += np.sum(p == t[i:i+k])를 통해 확인하고 점수를 계산하게 됩니다.